The objective for the Physics Derivation Graph project is to write down
all known mathematical physics in a way that can be both read by humans and
checked by a computer algebra system. To do that, primary design considerations
include how to represent the objects
(e.g., inference rules
and expressions
and symbols) and what data structure is sufficient for the objective.
This page describes the current status and historical evoluation of design
decisions critical to the Physics Derivation Graph.
In the Physics Derivation Graph, the primary vocabulary is a set of
inference rules that relate mathematical expressions.
The grammar of the Physics Derivation Graph is specified by this list, with all items joined by "and":
The Physics Derivation Graph is a set of derivations.
The visualization of a graph with expressions and inference rules as nodes
relies on each node having a distinct index.
Each expression, symbol, and inference rule appears only once in the database.
This is made possible through use of unique IDs associated with every facet of the visualization.
To see what this means in terms of the "period and frequency"
example on the homepage,
here is a view of the indices supporting that visualization for two sequential steps:
Figure 1. Two steps with all numeric IDs shown.
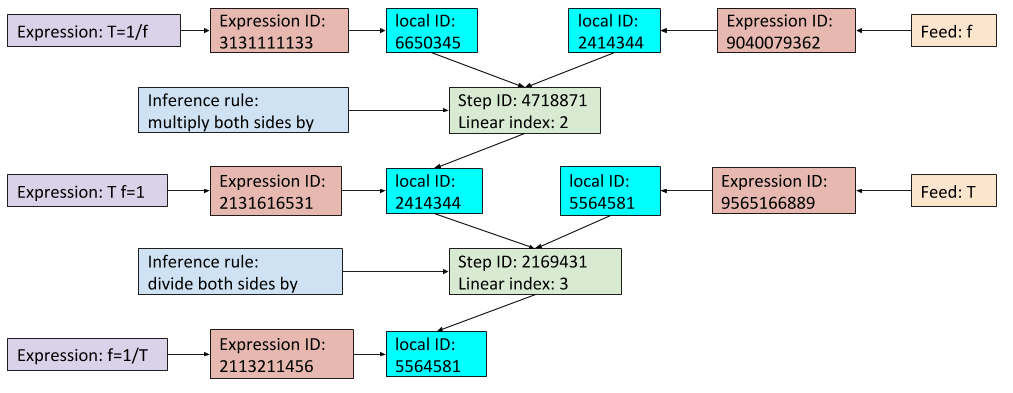
Manipulating these indices underlies all other tasks in the Physics Derivation Graph.
Access to these indices is performed through a single data structure.
The Physics Derivation Graph is currently stored in a single JSON file. The JSON file is read into Python as a dictionary.
JSON is convenient because it is plain text and the ease of detailed validation available using schemas.
The many alternatives to JSON (e.g., SQLite, Redis, Python Pickle, CSV, GraphML) offer trade-offs, a few of which have been explored.
There are multiple choices of how to represent a mathematical expression.
The choices feature trade-offs between conciseness, ability to express the range of notations necessary for Physics, symantic meaning, and ability to use the expression in a computer algebra system (CAS).
See the comparison of syntax below.
\(\rm\LaTeX\) was selected primarily because of the common use in Physics, display of complex math, conciseness, and expressiveness.
The use of \(\rm\LaTeX\) means other tasks like parsing symbols and resolving ambiguity are harder.
A reasonable question is, "Why is the Physics Derivation Graph complicated?"
To answer that, let's walk through the process of tracking information used in a derivation.
A simple derivation is the transition from the expression \(T = 1/f\) to \(f = 1/T\), the same example used on the home page.
The purpose of this section is to explain how a graph relates to the steps associated with this math.
The steps needed to make the transformation are to multiply both sides by \(f\), then divide both sides by \(T\).
There are four steps in this derivation:
declare initial expression \(T=1/f\)
multiply both sides of \(T=1/f\) by \(f\) to get \(T*f=1\)
divide both sides of \(T f=1\) by \(T\) to get \(f=1/T\)
declare final expression: \(f=1/T\)
This expansion to atomic steps is not typically documented.
This expansion can be tedious for derivations, but it is necessary for validation of steps using a Computer Algebra System.
As a recommendation, starting the derivation on paper and then expanding to atomic steps with inference rules is best done on paper.
The next step is to visualize this graph.
When building a graph, there are three types of nodes: inference rules, expressions, and feeds.
The graph will only have three types of directed edges:
from "inference rule" to "expression"
from "expression" to "inference rule"
from "feed" to "inference rule"
Although there is enough information present to generate a graph, the objective for the Physics Derivation Graph is to support more complex derivations and to link multiple derivations.
In the Physics Derivation Graph the inference rule "multiply both sides by" may appear in multiple steps.
The graph should not render multiple uses of the same inference rule as the same node.
Multiple references to the same expression should be a single node.
Therefore, an index which has a scope limited to the local derivation step is needed.
This leads to the notion of a unique numeric index local to each inference rule.
The local index for the inference rule is a unique identifier within a derivation step.
Another complication arises regarding the expressions.
The usefulness of \(T = 1/f\) depends on what is reading the expression.
Multiple readers of the expression can be expected: humans, LaTeX, and Computer Algebra Systems (e.g., Mathematica, Sympy).
This leads to the need for a unique identifier which is associated with the expression independent of the representation.
In Logic, this unique identifier is referred to as the Godel number.
Similarly, the "feeds" (here f and T need unique identifiers.
To summarize the above points,
each inference rule gets a local identifier
each expression gets a unique identifier
each feed gets a unique identifier
The expression index is the same across all derivations, whereas the local index is scoped to just the derivation step.
Similarly, the inference rule index is specific to the derivation step.
The inference rule needs the local index to build the graph.
The expression needs a local index to build the \(\rm\LaTeX\) PDF.
In addition to the inference rules and expressions, each \(\rm\LaTeX\) expression actually represents an Abstract Syntax Tree (AST) composed of symbols.
Figure 4. All of the jargon used and the relation between jargon used in the Physics Derivation Graph.
The Physics Derivation Graph has progressed through multiple architectures, with data structure changes keeping pace with the developer's knowledge.
plain text:
databases for comments, connections, equations, operators. Perl script to convert database content to images.
One line per entry in each database.
web interface:
the current implementation.
Uses Python, Flask, Docker.
Data is stored in a JSON file.
Limited support for checking inference rules using Sympy.
Storage formats evolved:
nested Python dictionaries and lists stored as a Python Pickle
nested Python dictionaries and lists stored as a JSON file. With this approach the schema can be validated
nested Python dictionaries and lists stored as a JSON file stored in Redis. Retains the schema validation of JSON while preventing concurrent writes to file; see https://redis.io/topics/transactions
nested Python dictionaries and lists stored as a JSON file stored in SQLite3. Part of the migration towards table-based implementation. SQLite3 is better than Redis because Redis requires a Redis server to be running whereas SQLite3 is a file.
Each of these have required a rewrite of the code from scratch, as well as transfer code (to move from n to n+1).
The author didn't know about property graphs when implementing v1, v2, and v3.
Within a given implementation, there are design decisions with trade-offs to evaluate.
Knowing all the options or consequences is not feasible until one or more are implemented.
Then the inefficiencies can be observed.
Knowledge gained through evolutionary iteration is expensive and takes a lot of time.
A few storage methods were considered and then rejected without a full implementation.
The Physics Derivation Graph can be expressed in RDF.
Each step in a derivation could be put in the subject–predicate–object triple form. For example, suppose the step is
Input 1: y=mx+b
inference rule: multiply both sides by
feed: 2
output 2: 2*y = 2*m*x + 2*b
Putting this in RDF,
step 1 | has input | y=mx+b
step 1 | has inference rule | multiply both sides by
step 1 | has feed | 2
step 1 | has output | 2*y = 2*m*x + 2*b
While it's easy to convert, I am unaware of the advantages of using RDF.
The Physics Derivation Graph is oriented towards visualization.
SPARQL is the query language for RDF. I don't see much use for querying the graph.
Using RDF doesn't help with using a computer algebra system for validation of the step.
Here methods of capturing mathematical syntax required to describe derivations in physics are compared.
This survey covers \(\rm\LaTeX\), Mathematical Markup Language (MathML), Mathematica, and SymPy.
For MathML, both Presentation and Content forms are included.
Although \(\rm\LaTeX\) is intuitive for scientists and is concise, it is a typesetting language and not well suited for the web or use in Computer Algebra Systems (CAS). Mathematica is also concise and has wide spread use by scientists, though its cost limits accessibility. Mathematica is also proprietary, which limits the ability to explore the correctness of this CAS
\(\rm\LaTeX\) is concise and is widely used in the scientific community. It does not work well for portability to other representations and is ill-suited for use by CAS. For the initial phases of development for the Physics Derivation Graph, portability and compatibilty with a CAS are not the priority. Since getting content into the graph is the priority, the Latex representation will be used.
For this survey it is assumed that users cares about the learning curve, leveraging previous experience, how wide spread use in their community, speed, ease of input, presentation (rendering), ability to access content across devices, OS independence, ease of setup.
To evaluate criteria relevant to users, including the ability to manually input syntax, the ability to transform between representations, and the ability to audit correctness.
Use of a single syntax for the graph content is important. To illustrate why, consider the approach where each syntax is used for its intended purpose -- Latex for rendering equation, SymPy for the CAS, and MathML for portability. This introduces a significant source of error when a single equation requires three distinct representation. The manual entry could result in the three representations not being sychronized. Thus, a single representation satisfying multiple criteria is needed. If no single syntax meets all the needs of the Physics Derivation Graph, then the requirements must be prioritized.
This comparison is between syntax methods which do not serve the same purpose. Latex is a type-setting language, while Mathematica and SymPy are Computer Algebra Systems (CAS). The reason these approaches for rendering and CAS were picked is twofold: they are widely used in the scientific community and they address requirements for the Physics Derivation Graph.
We can ignore syntax methods which do not support notation necessary for describing physics. Example of this include ASCII and HTML. Storage of the generated content (essentially a knowledge base for all of physics) isn't expected to exceed a Gigabyte, so compactness in terms of storage isn't a criterion in this evaluation.
to demonstrate the variety of uses in distinct domains of Physics, a set of test cases are provided in this section. These cases are not meant to be exhaustive of either the syntax or the scientific domain. Rather, they are examples of both capability requirements of the Physics Derivation Graph and of the syntax methods.
Case 1 is a second order polynomial. Algebra
\begin{equation}
a x^2 + b x + c = 0
\label{eq:polynomial_case1_body}
\end{equation}
Case 2, Stokes' theorem, includes integrals, cross products, and vectors. Calculus
\begin{equation}
\int \int_{\sum} \vec{\nabla} \times \vec{F} \dot d\sum = \oint_{\partial \sum} \vec{F}\dot d\vec{r}
\label{eq:stokes_case2_body}
\end{equation}
Case 3: Tensor analysis. Einstein notation: contravariant = superscript, covariant = subscript. Used in electrodynamics
\begin{equation}
Y^i(X_j) = \delta^i_{\ j}
\label{eq:tensor_analysis_case3_body}
\end{equation}
Case 4 covers notation used in Quantum Mechanics. Symbols such as \(\hbar\) and Dirac notation are typically used.
Case 4a is the creation operator
\begin{equation}
\hat{a}^+ |n\rangle = \sqrt{n+1} |n+1\rangle
\label{eq:creation_operator_case4a_body}
\end{equation}
Case 4b is the uncertainty principle
\begin{equation}
\sigma_x \sigma_p \geq \frac{\hbar}{2}
\label{eq:uncertainty_principle_case4b_body}
\end{equation}
MathML is comprised of empty elements (symbols, e.g., <plus/>), token elements (both ASCII and entities), and annotation elements.
The token elements in Presentation MathML include mi=identifiers, mn=numbers, mo=operators.
The token elements in Content MathML include ci=identifiers and cn=numbers.
Character count for the MathML was carried out using
Latex, MathML, and SymPy are free and open source. Mathematica is proprietary and not free.
For Physicists comfortable writing journal articles in Latex or exploring ideas in Mathematica, these are natural syntax methods. Both Latex and Mathematica are concise, making them intuitive to read and quick to enter. MathML is a verbose syntax which is lengthy to manually enter and yield difficult to read the native XML.
Unicode is needed to support Dirac notation and any other non-ASCII text in MathML
Wolfram Research offers the ability to convert from Mathematica expressions to MathML on their site www.mathmlcentral.com/Tools/ToMathML.jsp.
A CAS typically produces output syntax such as Latex or MathML in a single format. However, there are often many ways to represent the same math, equation \ref{eq:example_partial_derivative_representations}.
Latex and Presentation MathML are intended for rendering equations and are not easily parsed consistently by a CAS. For example, scientists and mathematicians often render the same partial differential operation in multiple ways:
\begin{equation}
\frac{\partial^2}{\partial t^2}F =
\frac{\partial}{\partial t}\frac{\partial F}{\partial t} =
\frac{\partial^2 F}{\partial t^2} =
\frac{\partial}{\partial t}\dot{F} =
\frac{\partial \dot{F}}{\partial t} = \ddot{F}.
\label{eq:example_partial_derivative_representations}
\end{equation}
All of these are equivalent.
The motives for using Sympy are the cost (free), the code (open source), the integration (Python), support for Physics, and the support for parsing Latex.
Although the Physics Derivation Graph is intended to be comprehensive
across domains, there are aspect of Physics not within the current scope of the project:
inclusion of graphics, e.g. free body diagrams, Feynman diagrams, geometrical diagrams.
explanatory text,
animations of concepts,
experimental processes,
interactive models.
These aspects could be included if the data structure and workflow were adapted
to an expanded scope.
