Welcome to the Physics Derivation Graph

MESSAGES:

list index out of range
list index out of range
list index out of range
list index out of range

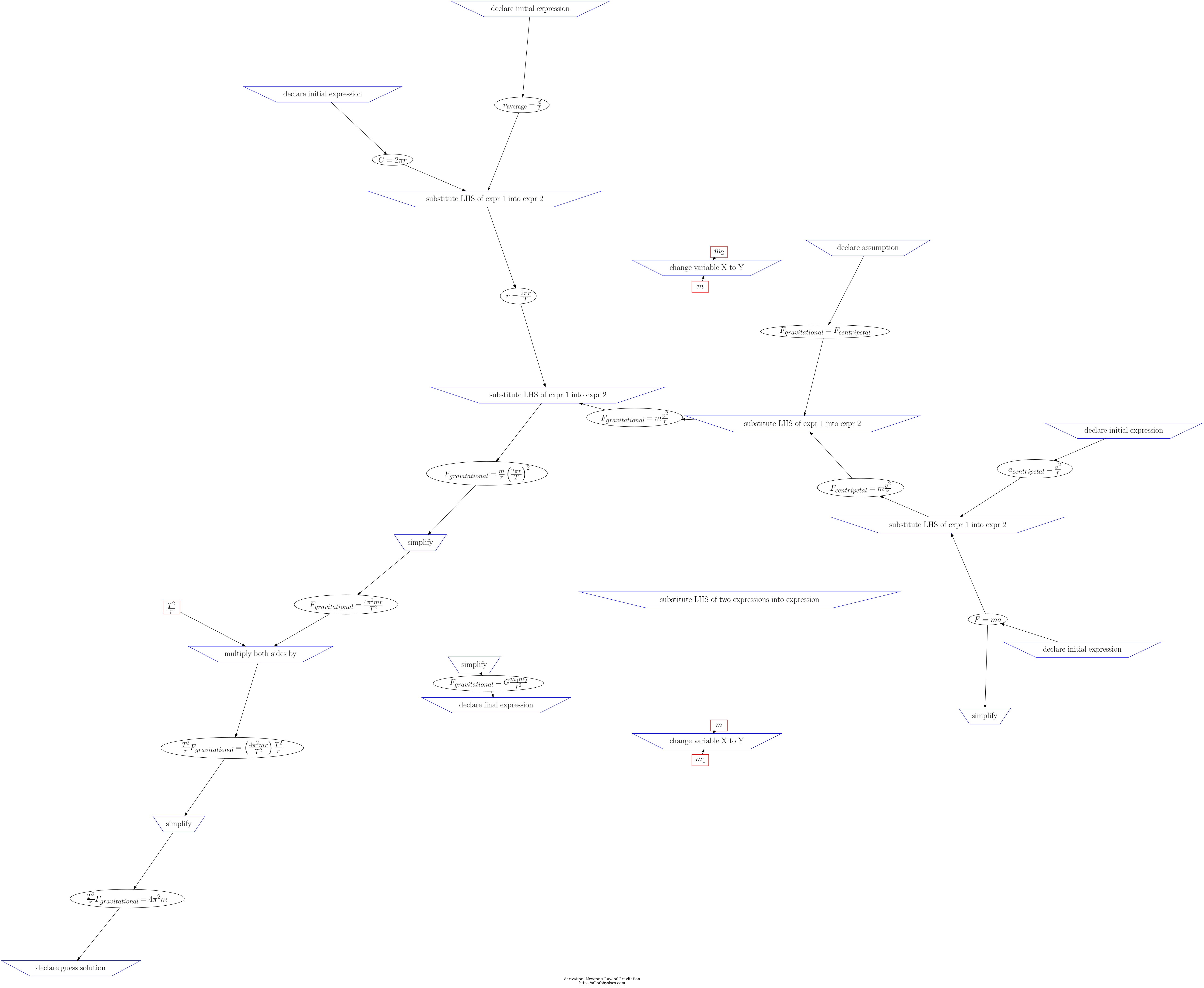
Return to navigation page or list derivations

Review Newton's Law of Gravitation

abstract: from https://www.youtube.com/watch?v=fJYdFIZlD8k
reference:

step	inference rule	input	feed	output	validity (as per SymPy)
17	ID: 111732; substitute LHS of two expressions into expression number of inputs: 3; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} and LHS of Eq.~\\ref{eq:#2} into Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.				recognized infrule but not yet supported
8	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	4820320578 $F_{gravitational}=F_{centripetal}$ 6026694087 $F_{centripetal}=m \frac{v^2}{r}$		4267808354 $F_{gravitational}=m \frac{v^2}{r}$	LHS diff is pdg0001687 - pdg0002867 RHS diff is pdg0005156(-pdg00013572 + v*2)/pdg0002530
10	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			6785303857 $C=2 \pi r$	no validation is available for declarations
9	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3411994811 $v_{\rm average}=\frac{d}{t}$	no validation is available for declarations
5	ID: 111104; declare assumption number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an assumption.			4820320578 $F_{gravitational}=F_{centripetal}$	no validation is available for declarations
19	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	1292735067 $F_{gravitational}=G \frac{m_1 m_2}{r^2}$			no validation is available for declarations
7	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5345738321 $F=m a$ 8361238989 $a_{centripetal}=\frac{v^2}{r}$		6026694087 $F_{centripetal}=m \frac{v^2}{r}$	LHS diff is a_{c(e(n(t(r(i(p(e(t(al)))))))))} - pdg0001687 RHS diff is (pdg0001357*2 - pdg0005156v**2)/pdg0002530
15	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	3004158505 $\frac{T^2}{r} F_{gravitational}=\left( \frac{4 \pi^2 m r}{T^2} \right)\frac{T^2}{r}$		3650370389 $\frac{T^2}{r} F_{gravitational}=4 \pi^2 m$	valid
11	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	6785303857 $C=2 \pi r$ 3411994811 $v_{\rm average}=\frac{d}{t}$		5177311762 $v=\frac{2 \pi r}{T}$	LHS diff is -pdg0001357 + pdg0006709 RHS diff is -2pdg0002530pdg0003141/pdg0008762 + pdg0001943/pdg0001467
3	ID: 111886; change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.		3876446703 $m$ 7905984866 $m_1$		list index out of range
18	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.			1292735067 $F_{gravitational}=G \frac{m_1 m_2}{r^2}$	list index out of range
13	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	6268336290 $F_{gravitational}=\frac{m}{r}\left(\frac{2\pi r}{T}\right)^2$		7672365885 $F_{gravitational}=\frac{4 \pi^2 m r}{T^2}$	valid
14	ID: 111182; multiply both sides by number of inputs: 1; feeds: 1; outputs: 1 Multiply both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	7672365885 $F_{gravitational}=\frac{4 \pi^2 m r}{T^2}$	3448601530 $\frac{T^2}{r}$	3004158505 $\frac{T^2}{r} F_{gravitational}=\left( \frac{4 \pi^2 m r}{T^2} \right)\frac{T^2}{r}$	LHS arithmetic error. Diff: pdg0002867(-pdg00087622 + pdg0009491*2)/pdg0002530
1	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			5345738321 $F=m a$	no validation is available for declarations
6	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8361238989 $a_{centripetal}=\frac{v^2}{r}$	no validation is available for declarations
4	ID: 111886; change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.		9594072504 $m_2$ 2346952973 $m$		list index out of range
12	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	4267808354 $F_{gravitational}=m \frac{v^2}{r}$ 5177311762 $v=\frac{2 \pi r}{T}$		6268336290 $F_{gravitational}=\frac{m}{r}\left(\frac{2\pi r}{T}\right)^2$	LHS diff is pdg0001357 - pdg0002867 RHS diff is 2pdg0002530pdg0003141(-2pdg0003141pdg0004851 + pdg0008762)/pdg0008762*2
16	ID: 111237; declare guess solution number of inputs: 1; feeds: 0; outputs: 1 Judicious choice as a guessed solution to Eq.~\\ref{eq:#1} is Eq.~\\ref{eq:#2},	3650370389 $\frac{T^2}{r} F_{gravitational}=4 \pi^2 m$			no validation is available for declarations
2	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	5345738321 $F=m a$			list index out of range

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.005 seconds for pdg_app/to_review_derivation: node_properties, derivation4936456
0.013 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation5357760
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8992289
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8992289
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8992289
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8992289
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_sequence_index5357760
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9834234
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9834234
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9834234
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9834234
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8941520
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8941520
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8941520
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8941520
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9368681
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9368681
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9368681
0.014 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9368681
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3869958
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3869958
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3869958
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3869958
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2226543
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2226543
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2226543
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2226543
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2997544
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2997544
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2997544
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2997544
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2018963
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2018963
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2018963
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2018963
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3105530
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3105530
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3105530
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3105530
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7539349
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7539349
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7539349
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7539349
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4928332
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4928332
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4928332
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4928332
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2311271
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2311271
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2311271
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2311271
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2436026
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2436026
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2436026
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2436026
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5899499
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5899499
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5899499
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5899499
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2906861
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2906861
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2906861
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2906861
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3727248
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3727248
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3727248
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3727248
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2724576
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2724576
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2724576
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2724576
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4284793
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4284793
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4284793
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4284793
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9301115
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9301115
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9301115
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9301115
0.007 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation4936456
0.008 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id4936456207210
0.035 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule4936456
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6360406
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6360406
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6360406
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6360406
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5213768
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5213768
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5213768
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5213768
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4714076
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4714076
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4714076
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4714076
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8757378
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8757378
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8757378
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8757378
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1316154
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1316154
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1316154
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1316154
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5470979
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5470979
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5470979
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5470979
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6169337
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6169337
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6169337
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6169337
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8835307
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8835307
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8835307
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8835307
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9259894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9259894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9259894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9259894
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8387412
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8387412
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8387412
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8387412
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1227538
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1227538
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1227538
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1227538
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8014152
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8014152
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8014152
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8014152
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5279402
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5279402
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5279402
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5279402
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6798334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6798334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6798334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6798334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2457878
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2457878
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2457878
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2457878
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6646149
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6646149
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6646149
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6646149
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9778832
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9778832
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9778832
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9778832
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1819804
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1819804
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1819804
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1819804
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8238767
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8238767
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8238767
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8238767
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7090212
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7090212
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7090212
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7090212
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4329620
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4329620
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4329620
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4329620
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1123077
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1123077
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1123077
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1123077
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2402608
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2402608
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2402608
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2402608
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4493423
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4493423
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4493423
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4493423
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1428619
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1428619
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1428619
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1428619
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9528704
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9528704
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9528704
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9528704
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2399907
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2399907
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2399907
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2399907
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5333537
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5333537
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5333537
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5333537
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4281143
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4281143
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4281143
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4281143
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4723867
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4723867
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4723867
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4723867
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1966039
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1966039
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1966039
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1966039
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6028048
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6028048
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6028048
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6028048
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6441560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6441560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6441560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6441560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1608693
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1608693
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1608693
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1608693
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8970397
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8970397
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8970397
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8970397
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4748635
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4748635
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4748635
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4748635
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3537104
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3537104
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3537104
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3537104
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8870579
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8870579
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8870579
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8870579