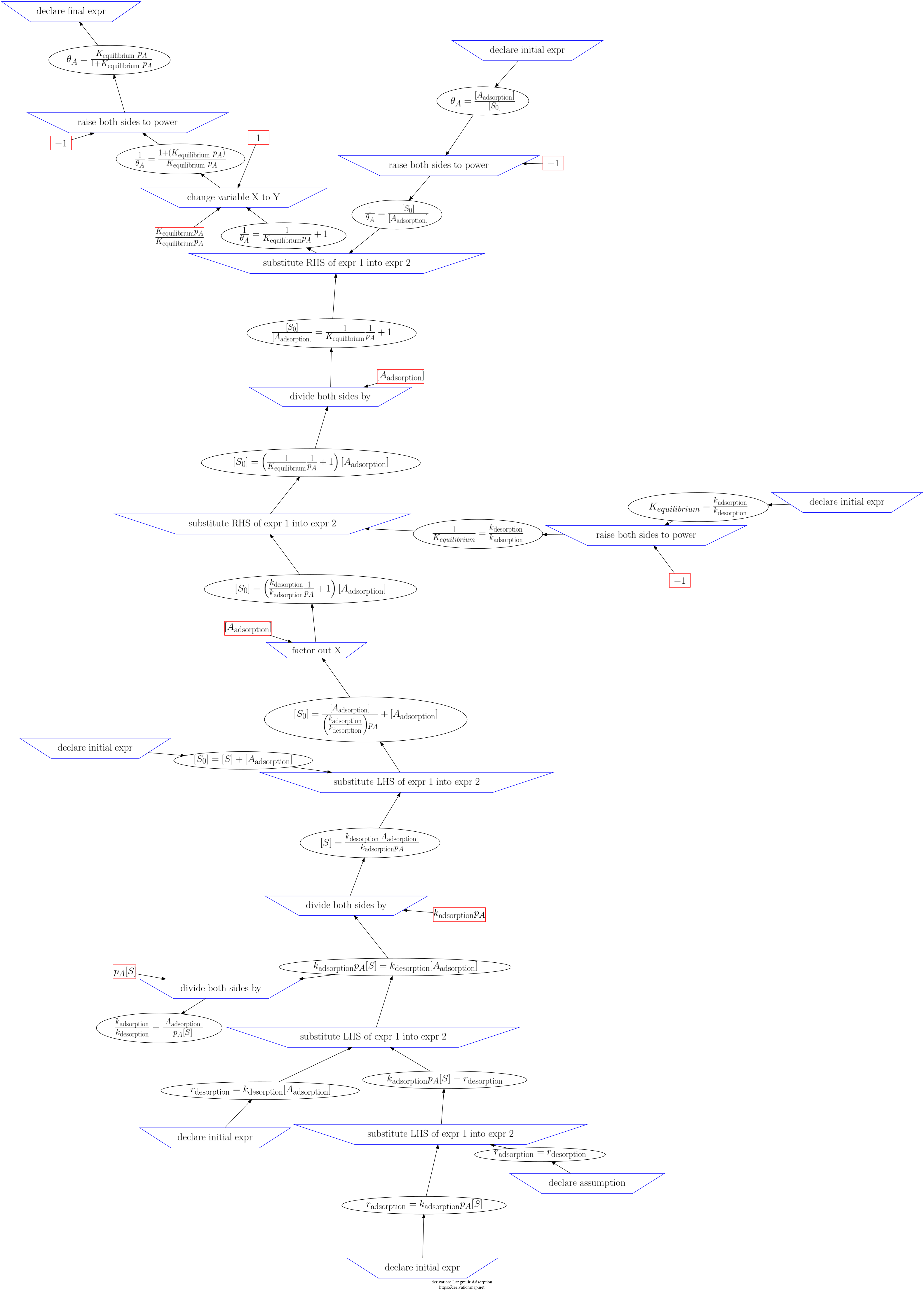
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
from https://arxiv.org/pdf/2210.12150.pdf
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 10 | divide both sides by |
|
|
|
LHS diff is pdg6850 - pdg6850/pdg8379 RHS diff is pdg4940*(pdg8379 - 1)/(pdg9046*pdg9067) |
3488423948:
5085809757: |
3488423948:
5085809757: |
|
| 11 | declare initial expr |
|
|
|
no validation is available for declarations |
7924063906:
|
7924063906:
|
definition of equilibrium |
| 6 | divide both sides by |
|
|
|
valid |
3488423948:
9562264720: |
3488423948:
9562264720: |
|
| 16 | raise both sides to power |
|
|
|
no check is performed |
2114909846:
8131665171: |
2114909846:
8131665171: |
|
| 12 | raise both sides to power |
|
|
|
no check is performed |
7924063906:
6240546932: |
7924063906:
6240546932: |
|
| 18 | change variable X to Y |
|
|
|
valid |
7928111771:
7267424860: |
7928111771:
7267424860: |
|
| 14 | divide both sides by |
|
|
|
valid |
7517073655:
6457999644: |
7517073655:
6457999644: |
|
| 17 | substitute RHS of expr 1 into expr 2 |
|
|
|
valid |
8131665171:
6457999644: 7928111771: |
8131665171:
6457999644: 7928111771: |
|
| 19 | raise both sides to power |
|
|
|
no check is performed |
7267424860:
4689334676: |
7267424860:
4689334676: |
|
| 3 | declare assumption |
|
|
|
no validation is available for declarations |
6783009163:
|
6783009163:
|
|
| 5 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
6955192897:
3507029294: 3488423948: |
6955192897:
3507029294: 3488423948: |
|
| 15 | declare initial expr |
|
|
|
no validation is available for declarations |
2114909846:
|
2114909846:
|
|
| 4 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
3736177473:
inconsistent dimensions 6783009163: 3507029294: |
3736177473:
N/A 6783009163: 3507029294: |
|
| 2 | declare initial expr |
|
|
|
no validation is available for declarations |
6955192897:
|
6955192897:
|
|
| 20 | declare final expr |
|
|
|
no validation is available for declarations |
4689334676:
|
4689334676:
|
|
| 7 | declare initial expr |
|
|
|
no validation is available for declarations |
3599953931:
|
3599953931:
|
The concentration of all sites by summing the concentration of free sites [S] and occupied sites |
| 8 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
9562264720:
3599953931: 4301729661: |
9562264720:
3599953931: 4301729661: |
|
| 9 | factor out X |
|
|
|
valid |
4301729661:
2168306601: |
4301729661:
2168306601: |
|
| 13 | substitute RHS of expr 1 into expr 2 |
|
|
|
valid |
6240546932:
2168306601: 7517073655: |
6240546932:
2168306601: 7517073655: |
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
3736177473:
inconsistent dimensions |
3736177473:
N/A |
| symbol ID | category | latex | scope | dimension | name | value | Used in derivations | references | |
|---|---|---|---|---|---|---|---|---|---|
| 9067 | variable |
[S]
\([S]\) |
real |
|
concentration of free sites in number per square meter | 7 | |||
| 1966 | variable |
r_{\rm desorption}
\(r_{\rm desorption}\) |
real |
|
rate of desorption | 3 | |||
| 9046 | variable |
p_A
\(p_A\) |
real | dimensionless | partial pressure of A over the surface | 15 | |||
| 6850 | variable |
k_{\rm adsorption}
\(k_{\rm adsorption}\) |
real | dimensionless | constant of forward adsorption reaction | 10 | |||
| 1791 | variable |
\theta_A
\(\theta_A\) |
real | dimensionless | the fraction of the surface sites covered with A | 5 | |||
| 6687 | variable |
r_{\rm adsorption}
\(r_{\rm adsorption}\) |
real |
|
rate of adsorption | 2 | |||
| 3037 | variable |
[S_0]
\([S_0]\) |
real |
|
total number of sites | 7 | |||
| 8379 | variable |
k_{\rm desorption}
\(k_{\rm desorption}\) |
real | dimensionless | constant of backward desorption reaction | 8 | |||
| 4940 | variable |
[A_{\rm adsorption}]
\([A_{\rm adsorption}]\) |
real |
|
surface concentration of A in molecules per square meter | 13 | |||
| 4933 | variable |
K_{\rm equilibrium}
\(K_{\rm equilibrium}\) |
real | dimensionless | constant for equilibrium when rate of adsorption equals the rate of desorption | 8 |