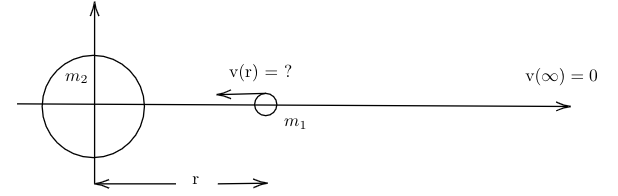
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
|
Explanation: often steps are skipped in conveying a derivation. To facilitate formal validation, the implicit steps need to be documented. Who does this work: human content creator Motive for doing this work: clearer explanation of mathematical steps. Facilitates student learning and reproducibility in a research context. |
Navigation:
|
source: "Derivation of Gravitational Potential Energy" by Rhett Allain
Suppose an object starts an infinite distance from a moon and is dropped, falling towards the moon due to gravitational acceleration. What is the speed of the object when it is distance \(r\) from the moon?
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
The initial conditions are \begin{equation} v(x=\infty) =0 \label{eq:initial_velocity} \end{equation} The force acting on the object is \begin{equation} \vec{F} = \frac{-G m_1 m_2}{x^2} \hat{x} \label{eq:gravitational force} \end{equation} The work is calculated using W_{\rm to\ system} = \(\Delta E\) since the force changes. To find the cumulative work done on the object, integrate over all positions between \(\infty\) and \(r\) \begin{equation} W_{\rm to\ system} = \int_{\infty}^r \vec{F}\cdot d\vec{r} \label{eq:work as function of force} \end{equation} Substituting the gravitational force into Eq. \ref{eq:work as function of force}, \begin{equation} W_{\rm to\ system} = \int_{\infty}^r \frac{-G m_1 m_2}{x^2} dx \end{equation} Factor out the constants, \begin{equation} W_{\rm to\ system} = -G m_1 m_2\int_{\infty}^r \frac{1}{x^2} dx \end{equation} \begin{equation} W = \frac{G m_1 m_2}{r} \end{equation} Another definition of work is that it is the change in energy for a system: \(W_{\rm by\ system} = \Delta KE \). Because the initial velocity was zero, the work here is \begin{equation} W_{\rm by\ system} = \frac{1}{2} m_1 v^2 \end{equation} Thus we can combine the two definitions of work to get \begin{equation} \frac{1}{2} m_1 v^2 = \frac{G m_1 m_2}{r} \end{equation} The \(m_1\) cancels, leaving \begin{equation} v(r) = \sqrt{\frac{2Gm_2}{r}} \end{equation}