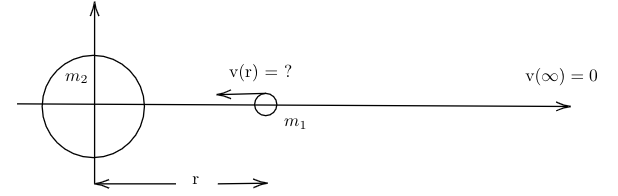
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
Explanation: This page shows the combination of tagging of sections, words, and expressions. I'm not sure whether there are more actions that could add structure. Perhaps Discourse Representation Theory? This illustrates the unreadability of the tagging. Normally the tags would not be visible to a reader. However, the editor of the content is exposed to this complexity. Who does this work: human content creator Motive for doing this work: ability to search documents |
Navigation:
|
source: "Derivation of Gravitational Potential Energy" by Rhett Allain
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="v=0" display="block"> <apply> <eq/> <ci>v</ci> <cn type="integer">0</cn> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="\vec{F}=\frac{-Gm_{1}m_{2}}{x^{2}}\hat{x}" display="block"> <apply> <eq/> <apply> <ci>→</ci> <ci>𝐹</ci> </apply> <apply> <times/> <apply> <divide/> <apply> <minus/> <apply> <times/> <ci>𝐺</ci> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">1</cn> </apply> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">2</cn> </apply> </apply> </apply> <apply> <csymbol cd="ambiguous">superscript</csymbol> <ci>𝑥</ci> <cn type="integer">2</cn> </apply> </apply> <apply> <ci>^</ci> <ci>𝑥</ci> </apply> </apply> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="W=\int_{\infty}^{r}\frac{-Gm_{1}m_{2}}{x^{2}}dx" display="block"> <apply> <eq/> <ci>𝑊</ci> <apply> <apply> <csymbol cd="ambiguous">superscript</csymbol> <apply> <csymbol cd="ambiguous">subscript</csymbol> <int/> <infinity/> </apply> <ci>𝑟</ci> </apply> <apply> <times/> <apply> <divide/> <apply> <minus/> <apply> <times/> <ci>𝐺</ci> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">1</cn> </apply> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">2</cn> </apply> </apply> </apply> <apply> <csymbol cd="ambiguous">superscript</csymbol> <ci>𝑥</ci> <cn type="integer">2</cn> </apply> </apply> <apply> <csymbol cd="latexml">differential-d</csymbol> <ci>𝑥</ci> </apply> </apply> </apply> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="W=-Gm_{1}m_{2}\int_{\infty}^{r}\frac{1}{x^{2}}dx" display="block"> <apply> <eq/> <ci>𝑊</ci> <apply> <minus/> <apply> <times/> <ci>𝐺</ci> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">1</cn> </apply> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">2</cn> </apply> <apply> <apply> <csymbol cd="ambiguous">superscript</csymbol> <apply> <csymbol cd="ambiguous">subscript</csymbol> <int/> <infinity/> </apply> <ci>𝑟</ci> </apply> <apply> <times/> <apply> <divide/> <cn type="integer">1</cn> <apply> <csymbol cd="ambiguous">superscript</csymbol> <ci>𝑥</ci> <cn type="integer">2</cn> </apply> </apply> <apply> <csymbol cd="latexml">differential-d</csymbol> <ci>𝑥</ci> </apply> </apply> </apply> </apply> </apply> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="W=\frac{Gm_{1}m_{2}}{r}" display="block"> <apply> <eq/> <ci>𝑊</ci> <apply> <divide/> <apply> <times/> <ci>𝐺</ci> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">1</cn> </apply> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">2</cn> </apply> </apply> <ci>𝑟</ci> </apply> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="W=\Delta KE" display="block"> <apply> <eq/> <ci>𝑊</ci> <ci>ΔKE</ci> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="W=\frac{1}{2}m_{1}v^{2}=\frac{Gm_{1}m_{2}}{r}" display="block"> <apply> <and/> <apply> <eq/> <ci>𝑊</ci> <apply> <times/> <apply> <divide/> <cn type="integer">1</cn> <cn type="integer">2</cn> </apply> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">1</cn> </apply> <apply> <csymbol cd="ambiguous">superscript</csymbol> <ci>𝑣</ci> <cn type="integer">2</cn> </apply> </apply> </apply> <apply> <eq/> <share href="#Ex1.m1.sh1"/> <apply> <divide/> <apply> <times/> <ci>𝐺</ci> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">1</cn> </apply> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">2</cn> </apply> </apply> <ci>𝑟</ci> </apply> </apply> </apply> </math>
<?xml version="1.0" encoding="UTF-8"?> <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="v=\sqrt{\frac{2Gm_{2}}{r}}" display="block"> <apply> <eq/> <ci>𝑣</ci> <apply> <root/> <apply> <divide/> <apply> <times/> <cn type="integer">2</cn> <ci>𝐺</ci> <apply> <csymbol cd="ambiguous">subscript</csymbol> <ci>𝑚</ci> <cn type="integer">2</cn> </apply> </apply> <ci>𝑟</ci> </apply> </apply> </apply> </math>