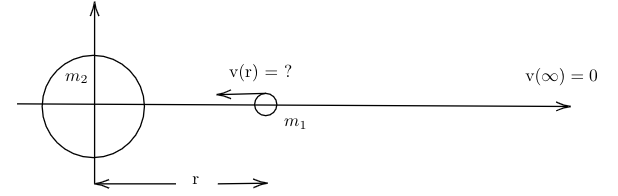
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
Explanation: Content MathML using the command latexmlmath --cmml=- "v=0"Not all of the nuances from each expression have been correctly translated in Content MathML. Some manual cleanup is required. Because this page uses MathJax, the Presentation MathML is available for each expression by right-clicking on any rendered expression and selecting "Show Math As" and then "MathML code". MathJax has an extension for generation of Content MathML but it is not available for v3 of MathJax as of August 2020. Who does this work: human using LatexML Motive for doing this work: preparation for use with Computer Algebra System. Caveat: no CAS currently consumes Content MathML as input. |
Navigation:
|
source: "Derivation of Gravitational Potential Energy" by Rhett Allain
Suppose an object starts an infinite distance from a moon and is dropped, falling towards the moon due to gravitational acceleration. What is the speed of the object when it is distance \(r\) from the moon?
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
The initial condition is
The force acting on the object is The work is calculated using W = \(\Delta E\) since the force changes. To find the cumulative work done on the object, integrate over all positions between \(\infty\) and \(r\) Substituting the gravitational force into Eq. \ref{eq:work as function of force}, Factor out the constants, which leads to Another definition of work is that it is the change in energy for a system: \(W = \Delta E \) Because the initial velocity was zero, the work here is Thus we can combine the two definitions of work to get The \(m_1\) cancels, leaving