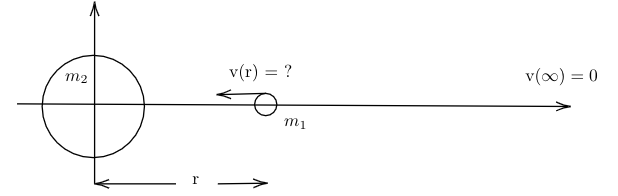
 Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
Explanation: Identify relevant words and Physics-specific keywords in each sentence.
Optionally, link these keywords to ScienceWise database or Wikipedia entry.
Who does this work: human content creator. Motive for doing this work: linking words as concepts to provide clear definition of terms. |
Navigation:
|
source: "Derivation of Gravitational Potential Energy" by Rhett Allain
Suppose an
an from a and is , the What is the of the is \(r\) from the Figure 1: small mass falling towards a moon from initial position at infinity.
Figure 1: small mass falling towards a moon from initial position at infinity.
The
is \begin{equation} v(x=\infty) =0 \label{eq:initial_velocity} \end{equation} The acting on the is \begin{equation} \vec{F} = \frac{-G m_1 m_2}{x^2} \hat{x} \label{eq:gravitational force} \end{equation} The is calculated using W = \(\Delta E\) since the changes. To find the cumulative done on the , integrate over all positions between \(\infty\) and \(r\) \begin{equation} W = \int_{\infty}^r \vec{F}\cdot d\vec{r} \label{eq:work as function of force} \end{equation} Substituting the into Eq. \ref{eq:work as function of force}, \begin{equation} W = \int_{\infty}^r \frac{-G m_1 m_2}{x^2} dx \end{equation} Factor out the constants, \begin{equation} W = -G m_1 m_2\int_{\infty}^r \frac{1}{x^2} dx \end{equation} which leads to \begin{equation} W = \frac{G m_1 m_2}{r} \end{equation} Another definition of is that it is the change in for a system: \(W = \Delta E \) Because the was , the here is \begin{equation} W = \Delta KE \end{equation} Thus we can combine the two definitions of to get \begin{equation} W = \frac{1}{2} m_1 v^2 = \frac{G m_1 m_2}{r} \end{equation} The \(m_1\) cancels, leaving \begin{equation} v(r) = \sqrt{\frac{2Gm_2}{r}} \end{equation}