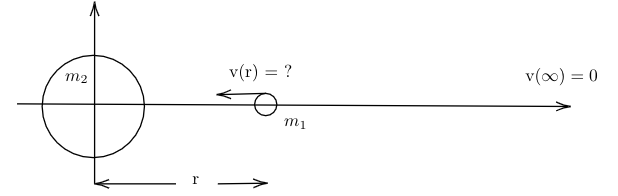
Figure 1: small mass falling towards a moon from initial position at infinity.
|
Explanation: Establishing the relation between keywords and symbols is distinct from tagging keywords and identifying symbols. Not all symbols will have a related keyword, as the author may rely on the reader to grasp the relation between symbol \(\infty\) and infinity. While some symbols like \(\infty\) are relatively standard, most symbols are overloaded. The context for a symbol may be only within a single paper. In this page the relation between "measure" and "symbol" pairs is illustrated visually. (The section, word, and expression tags have been suppressed for readability.) The underlying data structure for these relations could be a bipartite graph. Who does this work: human content creator Motive for doing this work: enabling machine parsing |
Navigation:
|
source: "Derivation of Gravitational Potential Energy" by Rhett Allain
Suppose an object starts an infinite distance from a moon and is dropped, falling towards the moon due to gravitational acceleration. What is the speed of the object when it is
from the moon?
Figure 1: small mass falling towards a moon from initial position at infinity.
The initial condition is \begin{equation} v(x=\infty) =0 \label{eq:initial_velocity} \end{equation} The force acting on the object is \begin{equation} \vec{F} = \frac{-G m_1 m_2}{x^2} \hat{x} \label{eq:gravitational force} \end{equation} The
is calculated using = \(\Delta E\) since the force changes. To find the cumulative work done on the object, integrate over all positions between \(\infty\) and \(r\) \begin{equation} W = \int_{\infty}^r \vec{F}\cdot d\vec{r} \label{eq:work as function of force} \end{equation} Substituting the gravitational force into Eq. \ref{eq:work as function of force}, \begin{equation} W = \int_{\infty}^r \frac{-G m_1 m_2}{x^2} dx \end{equation} Factor out the constants, \begin{equation} W = -G m_1 m_2\int_{\infty}^r \frac{1}{x^2} dx \end{equation} which leads to \begin{equation} W = \frac{G m_1 m_2}{r} \end{equation} Another definition of is that it is the for a system: = Because the initial velocity was zero, the work here is \begin{equation} W = \Delta KE \end{equation} Thus we can combine the two definitions of work to get \begin{equation} W = \frac{1}{2} m_1 v^2 = \frac{G m_1 m_2}{r} \end{equation} The \(m_1\) cancels, leaving \begin{equation} v(r) = \sqrt{\frac{2Gm_2}{r}} \end{equation}