What is the status of the project?
As of August 2024, a single developer is actively contributing to the project in his spare time. A few collaborators have previously contributed.
What is the durability of the project?
Many projects in knowledge management of science last as long as a grant or are created in support of a publication.
The Physics Derivation Grpah is hosted on DigitalOcean using a single droplet at a cost of $75/year.
As of August 2020, the account has $63 available (so at least another year).
The lease on the domain name through Google is $12/year and renews annually. Paid through 2030.
How do I add a new derivation? a new inference rule? a new expression? a new symbol?
All of these actions require being signed in using your Google account.
Local account and authenticating with other services (e.g. Github, Gitlab, Facebook) are not currently supported.
(If you want to advocate or request addition of a authentication site, submit a feature request.)
Once you are signed in, go to the navigation page. There is a link to "starting a new derivation". For inference rules, expressions, and symbols first go to the review page and then scroll to the bottom.
Why is a login required for some links and actions?
Static content is displayed for and accessible to anyone.
The ability to change the graph content requires a user to be signed in to prevent defacement and to track who contributed what in case a rollback is needed.

What graph queries are relevant to the Physics Derivation Graph?
What are alternative paradigms that yield the same artifacts?
These descriptions of the project are equivalent:
How does data entered into the site get to the Physics Derivation Graph github repo?
Content entered through the web interface is dumped into a JSON file
on the DigitalOcean virtual private server.
The project owner manually uploads code from that server to the github
repo for it to become part of the "official" source code.
Alternatively, a person could enter their derivation, download the
JSON file, and submit a pull request to the repo.
That process is not streamlined because submissions need to be manually reviewed prior to adding them. A user should not be able to add profanity or spam to the database.
What are the use cases for the Physics Derivation Graph?
| use case | who does the work? | who benefits? | pure Latex is sufficient? | incentive |
|---|---|---|---|---|
| show interconnectivity of expressions | project owner | students | yes | share the beauty of mathematical Physics |
| use PDG for derivation in paper appendix | paper author | paper readers | yes | none |
| validate homework derivation | student | student; teacher | no; CAS required | correctness of derivation |
| validate novel derivation | researcher | researcher | no; CAS required | correctness of derivation |
| database for training machine learning algorithms | project owner | machine learning researchers | no; CAS needed | progress in Physics? |
Each of these use cases involve significant amounts of tedious data entry and learning what inference rules exist and the interface to the Physics Derivation Graph.
If research grants do not require validation of math, then researchers are not motivated to invest. If promotion in academia does not depend on validation of math, then professors are not motivated to invest. If publishing research does not require validation of math, then authors are not motivated to invest. If students doing homework can get by without being correct, then students are not motivated to invest.
Could the Physics Derivation Graph serve as a central registration for symbols and expressions?
Yes! Or, even better, a separate platform could serve this purpose.
As two successful examples of central registration and tracking used in Science, consider the ORCID system for authors and DOIs for articles. Both of these examples seem to have originated with publishers.
ScienceWise is available for tracking of scientific words and phrases.
How to contribute to the Physics Derivation Graph?
How to contact the project owner?
Email is the best method: ben.is.located AT gmail.com
Also, there is a gitter channel available for developers.
The PDG Google Group is for community announcements, updates, summaries of status, documenting strategic decisions, and questions from users.
What is an inference rule?
Why does the user provide the input expressions, inference rule, and outputs? Why not generate the output from the inputs + inference rule?
In principle this is feasible in the Physics Derivation Graph.
With the user providing the input expressions and inference rules (plus any needed arguments), the outputs are deterministic.
For example, starting with the expression
\begin{equation}
a = b
\end{equation}
the user instructs the software to apply the inference rule "multiply both sides by x" where \(x=2\).
Then the software produces the output
\begin{equation}
2 a = 2 b
\end{equation}
The constraint is that the Computer Algebra System used in the PDG (SymPy) is not capable of handling all inference rules or all expressions.
Currently in the Physics Derivation Graph the user provides Latex, which gets converted (with help from the user) to SymPy.
SymPy may eventually have the capability of deterministically applying inference rules.
That would require investment in the Latex parser and Physics libraries.
Is the Physics Derivation Graph just knowledge management?
Yes. With some rigor to verify edges in the graph.
There have been similar efforts in Mathematical Knowledge Management.
What previous discussions of semantics in Physics exist?
A clear description of the issue of semantics in Physics expressions is presented in Making Meaning with Math in Physics: A semantic analysis and Language of physics, language of math: Disciplinary culture and dynamic epistemology.
The Physics Derivation Graph is enabled by sementic decoration of symbols and expressions. The implementation uses Sympy as a Computer Algebra System and extensive numeric indices for symbols, expressions, and steps.
Why would the Physics Derivation Graph succeed where other projects have stagnated?
This question is motivated by the essay "A Critique of OpenMath and Thoughts on Encoding Mathematics" (2001) since the Physics Derivation Graph is similar to the QED manifesto.
Rather than struggle to fit everything into a formal rigorous basis, the implementation for the Physics Derivation Graph uses Latex to encode math. Some expressions are represented using SymPy, with the hope that the Latex and SymPy refer to the same concepts.
By focusing on specific and practical demonstrations, the Physics Derivation Graph will provide value to teachers, students, and researchers.
What previous discussions of the grammar of Physics exists?
The grammar of physics by P. R. Subramanian, B. Gnanapragasam, and G. Janhavi
published in The Physics Teacher 28, 174 (1990); https://doi.org/10.1119/1.2342981. The focus seems to be on dimensional analysis.
There are also Science Ontologies like sciencewise.info
What domains does the Physics Derivation Graph cover?
What previous discussion of the syntax of Physics exists?
"syntax specifies exactly what should be allowed with regard to the formation of character strings." (source)
What is the role of proofs in the Physics Derivation Graph?
The Physics Derivation Graph does not prove anything; it merely documents the mathematical manipulations applied in Physics.
In this project a derivation is used to denote relations between statements that relate objective measurements of reality.
For more on this issue, see this answer.
Could the Physics Derivation Graph reduce Physics to axioms?
Relating the inference rules used in the Physics Derivation Graph to set theory or logical rules (e.g., modus ponens and axioms may be possible, but that is not in the current scope for the project.
How is the Physics Derivation Graph related to Computational Graphs in deep learning?
There is no relation between the inference rules and expressions present in the Physics Derivation Graph and computational graphs used in deep learning.
Does use of the Physics Derivation Graph and verification of steps in a derivation mean that the content is valid?
No. Simply carrying out mathematical manipulations of expressions does not necessarily lead to physically valid outcomes.
What lessons have you learned in implementing the Physics Derivation Graph?
My observations are specific to the nuances of the
project and my personality.
If you were starting from scratch, what would you have wished you had done differently?
Knowing what the requirements of the data structure up front would
have reduced the time wasted with insufficient data structures.
Better understanding where the Physics Derivation Graph fits with respect to semantics and formal proofs would have helped with finding relevant communities of practitioners. The Physics Derivation Graph fits with neither semantics nor proof assistants, but somewhere in between. I think I know how my work relates to mathematical proofs; I'm not clear how my work relates to semantic tagging and structures.
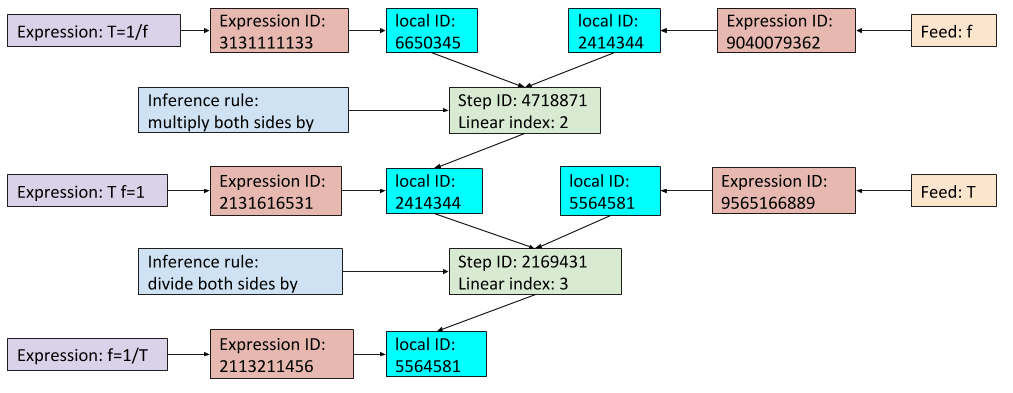
What's the purpose of the many numerical indices associated with the expressions and inference rules?
Each expression index is a Godel number.
This is a way of uniquely identifying each component in the graph.
Separate from that, a unique identifier is also need for inference rules to distinguish the use in different steps.
Is the Physics Derivation Graph research?
No new research in math or physics is needed to validate these claims.
This project documents the relations between derivations used to describe physical experiments.
Are there novel algorithms used in the Physics Derivation Graph?
There are no new algorithms.
The Physics Derivation Graph is about documenting existing knowledge.
How does the Physics Derivation Graph handle non-algebraic arguments?
The Physics Derivation Graph does not include geometric arguments.
The Physics Derivation Graph is similar to a Schuam's outline, except it is intended to cover all known Physics and documents the relations between various governing expressions.
Does the Physics Derivation Graph require that all users agree on the same notation?
No. A Latex symbol used in a derivation can be used anywhere else in the Physics Derivation Graph because numeric IDs are used to track the concept.
Are derivations in the Physics Derivation Graph representations?
What is the role of automation in the Physics Derivation Graph?
Don't Physics expressions share variables since they refer to the same reality?
What are the objectives for the Physics Derivation Graph?
Derivations used in Physics are mathematical expressions linked by a finite set of inference rules.
The purpose of this project is to test the claim that a finite static graph exists which relates all expressions of mathematical physics.
In this graph, nodes are expressions and edges are inference rules.
Expressions are typically placed in a topic within Physics. Conceptually, this would look like
A second claim to be tested is that a finite number of unique inference rules are needed to express the relations between expressions.
Who is the audience for the Physics Derivation Graph?
No. A step can be replaced by equivalent sequences of inference rules.
Various permutations of equivalent steps may be more or less efficient (in terms of number of steps), and more or less abstract conceptually.
There are no automatic mechanisms for generating new derivations.
There is some automation used in detecting symbols in a step or derivation.
Yes, a graph could be constructed that relies merely on variables that are common to expressions rather than derivations betweend expressions.
Conceptually, the view would be
Students,
teachers,
researchers.

Is there an alternative to the web interface for adding content?
There previously was a command-line prompt written in Python that facilitated content entry.
Investment in a command-line input tool was stopped and focus was shifted to an web-based input. Rendering the Latex and creating a graph of the content are not well-suited to the command line. I ended up always needing to open a PDF or a PNG or a webpage, so I decided to use the webpage for both input and review.
Is the Physics Derivation Graph a good way to learn Physics?
No. The project is not intended to facilitate education -- it is not a
replacement of textbooks which contain written explanations and pictures.
There is not a plan or expectation that teachers would use the Physics Derivation Graph to convey
knowledge to their students.
For tips on how to learn Physics,
(begin quote)
(end quote)
- Reading =/= understanding in math and physics. You understand a topic only if you can solve the problems.
- Work through the solved problems you encounter in textbooks carefully.
- Most people around me have never read any physics textbook cover to cover. E.g. reading Halliday, Resnick & Walker completely might take you years! Not all topics are equally important. Focus on the important parts.
- You need guidance on what is important and what is not. Online courses, college material (especially problem sets!), teaching webpages could be a helpful guide. MIT OCW is an excellent resource, once you are ready for it.
- Finding someone to talk to is really useful. You will likely have questions. Cultivating some relationship that allows you to ask questions is invaluable.
- College courses in math and physics have a very definitive order. It is really difficult to skip any step along the way. E.g. to understand special relativity, you must first understand classical physics and electrodynamics.
- Be prepared that the timescales in physics are long. Often, what turns people off is that they do not get things quickly (e.g. in 15-30 minutes). If you find yourself thinking hours about seemingly simple problems, do not despair! That is normal in physics.
- You have to 'soak in' physics. It takes time. Initially, you might feel like you do not make a lot of progress, but the more you know, the quicker it will get. Give yourself time and be patient and persistent.
- Often, just writing things down helps a lot with making things stick. It is a way of developing 'muscle memory'. So try and take notes while reading. Copying out solved problems from textbooks is also a good technique.
- Counterintuitive: If you get completely stuck, move on! Learning often happens in non-linear ways. If you hit an insurmountable roadblock, just keep going. When you return in a few days/weeks, things will almost certainly be clearer.
How could the Physics Derivation Graph be differentiated from the work of a crackpot?

How could the Physics Derivation Graph be used to identify the work of a crackpot?
If a crackpot is unable to quantiatively characterize their claims and make the assumptions explicit, then their work is less likely to be valid.
What is the output of the Physics Derivation Graph?
The output is typically a graph visualization or a PDF of the same content in a linear text format.
How can the Physics Derivation Graph be visualized?
The graph output can be visualized in a web browser, a static GraphViz output, and other formats.
How can the Physics Derivation Graph be checked?
A computer algebra system can be used to verify that each inference rule has been applied correctly to input and output expressions.
Specifically, SymPy is used to validate applications of inference rule.
How is the content of the Physics Derivation Graph stored?
The expressions, symbols, and connections are stored Latex in a JSON file.
This decision was based on a comparative analysis of other options, including MathML and Mathematica.
What subfields of Physics is this project capable of including?
Anything from Classical mechanics to Topological quantum field theory should be capable of being included.
What are the entry barriers to using the Physics Derivation Graph?
What is the Physics Derivation Graph not good at?
Can the Physics Derivation Graph be used to prove Physics?
No. "Proof" is not a well-defined term in Physics.
From a Stack Exchange answer,
Mathematical proofs relate to exactly how a MODEL will behave. They don't have much to do with how the real world behaves. If the mathematics is carried out correctly, then one has "proven" how the model will behave.The reason for experimentation, is to find out if the completely fictional MODEL that somebody simply made up, behaves in any way the same, as observations suggest the real world behaves. If it doesn't, that is not an indication of a mathematical error, it simply means the fictional model is not a good description of the real world, and must be changed.
Does this approach apply to other fields?
There is not clear application of the concepts used in the Physics Derivation Graph to other fields (ie chemistry, linguistics, economics, mathematics, etc).
The physics derivation graph can handle proving mathematical identities, ie Euler's equation, but that wasn't the intent.
The difference between a derivation and proving an identity is that when proving an identity, only one side of the equation is manipulated. For a derivation, both sides of the expression are involved.
How does the Physics Derivation Graph compare with other projects?
See the list of other projects
How could my project leverage the Physics Derivation Graph?
Collaboration can take the form of using the code to calling the API. Contact us for other options.