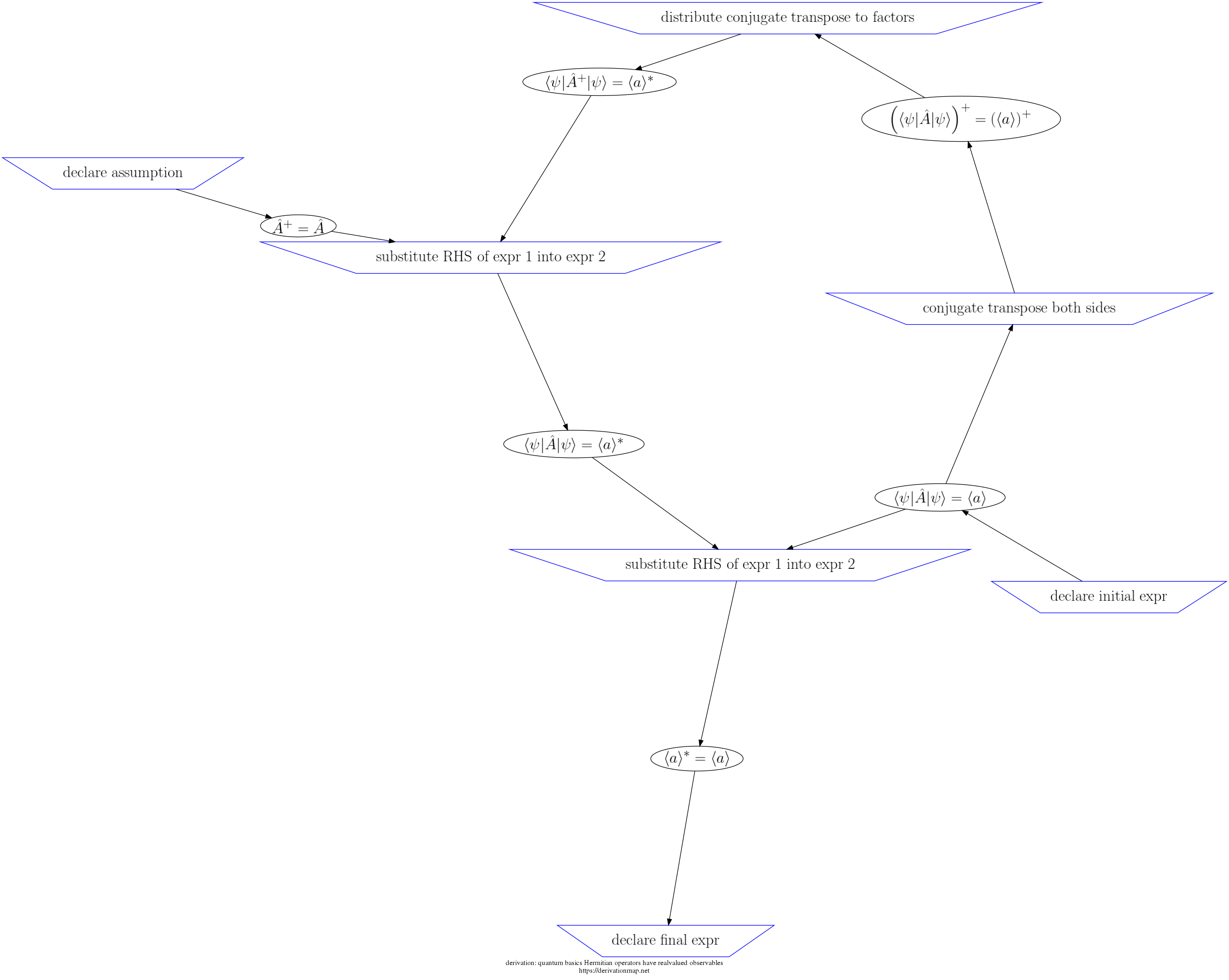
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 4 | declare assumption |
|
|
|
no validation is available for declarations |
9294858532:
|
9294858532:
|
|
| 3 | distribute conjugate transpose to factors |
|
|
|
Nothing to split |
2394935835:
no LHS/RHS split 1010393913: |
2394935835:
N/A 1010393913: |
|
| 5 | substitute RHS of expr 1 into expr 2 |
|
|
|
failed |
9294858532:
1010393913: 4948934890: |
9294858532:
1010393913: 4948934890: |
|
| 6 | substitute RHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
4948934890:
9999999975: no LHS/RHS split 2848934890: |
4948934890:
9999999975: N/A 2848934890: |
|
| 7 | declare final expr |
|
|
|
no validation is available for declarations |
2848934890:
|
2848934890:
|
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
9999999975:
no LHS/RHS split |
9999999975:
N/A |
|
| 2 | conjugate transpose both sides |
|
|
|
Nothing to split |
9999999975:
no LHS/RHS split 2394935835: no LHS/RHS split |
9999999975:
N/A 2394935835: N/A |
| symbol ID | category | latex | scope | dimension | name | value | Used in derivations | references | |
|---|---|---|---|---|---|---|---|---|---|
| 9329 | variable |
|\psi \rangle
\(|\psi \rangle\) |
complex | dimensionless | ket | 1 | |||
| 5598 | variable |
\hat{A}
\(\hat{A}\) |
real | dimensionless | observerable operator | 3 | |||
| 4065 | variable |
\langle \psi|
\(\langle \psi|\) |
complex | dimensionless | bra | 4 | |||
| 9139 | variable |
a
\(a\) |
['real'] | dimensionless | 45 |