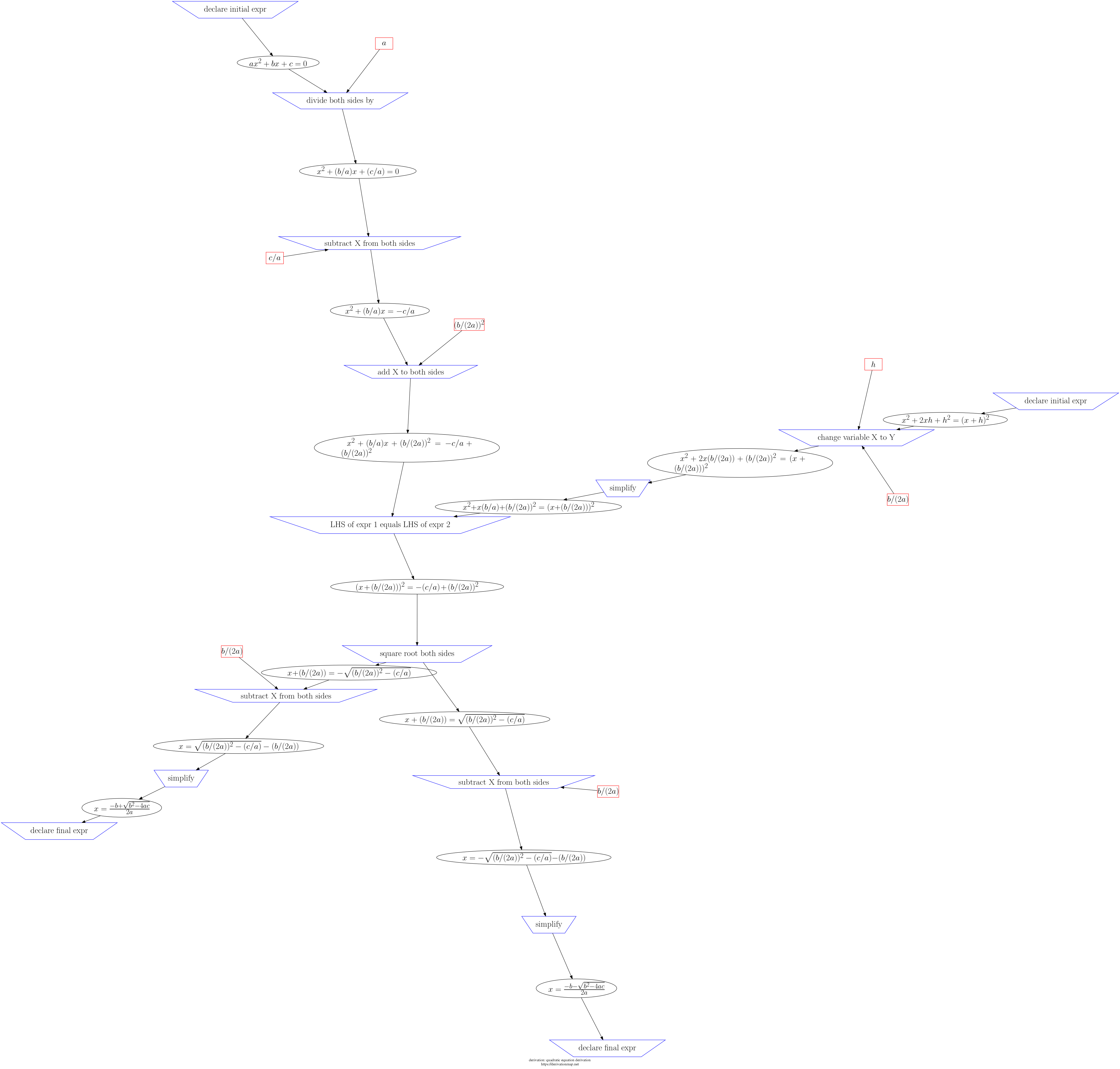
Physics Derivation Graph navigation Sign in

review derivation: quadratic equation derivation

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
https://en.wikipedia.org/wiki/Quadratic_formula#Derivations_of_the_formula

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
10 subtract X from both sides
  1. 5982958249; locally 6608123:
    \(x+(b/(2 a)) = -\sqrt{(b/(2 a))^2 - (c/a)}\)
    \(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}} = - \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
  1. 0002838490:
    \(b/(2 a)\)
    \(\frac{pdg_{1939}}{2 pdg_{9139}}\)
  1. 9582958293; locally 4433112:
    \(x = \sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)
    \(pdg_{1464} = - \frac{pdg_{1939}}{2 pdg_{9139}} + \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
LHS diff is 0 RHS diff is -sqrt((pdg1939**2 - 4*pdg4231*pdg9139)/pdg9139**2) 5982958249:
9582958293:
5982958249:
9582958293:
10.5 subtract X from both sides
  1. 9582958294; locally 6608102:
    \(x+(b/(2 a)) = \sqrt{(b/(2 a))^2 - (c/a)}\)
    \(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}} = \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
  1. 0002449291:
    \(b/(2 a)\)
    \(\frac{pdg_{1939}}{2 pdg_{9139}}\)
  1. 5982958248; locally 2657355:
    \(x = -\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)
    \(pdg_{1464} = - \frac{pdg_{1939}}{2 pdg_{9139}} - \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
LHS diff is 0 RHS diff is sqrt((pdg1939**2 - 4*pdg4231*pdg9139)/pdg9139**2) 9582958294:
5982958248:
9582958294:
5982958248:
11 simplify
  1. 5982958248; locally 2657355:
    \(x = -\sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)
    \(pdg_{1464} = - \frac{pdg_{1939}}{2 pdg_{9139}} - \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
  1. 9999999968; locally 8811221:
    \(x = \frac{-b-\sqrt{b^2-4ac}}{2 a}\)
    \(pdg_{1464} = \frac{- pdg_{1939} - \sqrt{pdg_{1939}^{2} - 4 pdg_{4231} pdg_{9139}}}{2 pdg_{9139}}\)
LHS diff is 0 RHS diff is (-pdg9139*sqrt((pdg1939**2 - 4*pdg4231*pdg9139)/pdg9139**2) + sqrt(pdg1939**2 - 4*pdg4231*pdg9139))/(2*pdg9139) 5982958248:
9999999968:
5982958248:
9999999968:
11.5 simplify
  1. 9582958293; locally 4433112:
    \(x = \sqrt{(b/(2 a))^2 - (c/a)}-(b/(2 a))\)
    \(pdg_{1464} = - \frac{pdg_{1939}}{2 pdg_{9139}} + \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
  1. 9999999969; locally 8761200:
    \(x = \frac{-b+\sqrt{b^2-4ac}}{2 a}\)
    \(pdg_{1464} = \frac{- pdg_{1939} + \sqrt{pdg_{1939}^{2} - 4 pdg_{4231} pdg_{9139}}}{2 pdg_{9139}}\)
LHS diff is 0 RHS diff is (pdg9139*sqrt((pdg1939**2 - 4*pdg4231*pdg9139)/pdg9139**2) - sqrt(pdg1939**2 - 4*pdg4231*pdg9139))/(2*pdg9139) 9582958293:
9999999969:
9582958293:
9999999969:
5 add X to both sides
  1. 5938459282; locally 1212129:
    \(x^2 + (b/a)x = -c/a\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} = - \frac{pdg_{4231}}{pdg_{9139}}\)
  1. 0004307451:
    \((b/(2 a))^2\)
    \(\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}}\)
  1. 5928292841; locally 1120000:
    \(x^2 + (b/a)x + (b/(2 a))^2 = -c/a + (b/(2 a))^2\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} + \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} = \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}\)
valid 5938459282:
5928292841:
5938459282:
5928292841:
4 subtract X from both sides
  1. 5958392859; locally 7777621:
    \(x^2 + (b/a)x+(c/a) = 0\)
    \(pdg_{1464}^{2} + pdg_{1464} + \frac{pdg_{4231}}{pdg_{9139}} = 0\)
  1. 0006644853:
    \(c/a\)
    \(\frac{pdg_{4231}}{pdg_{9139}}\)
  1. 5938459282; locally 1212129:
    \(x^2 + (b/a)x = -c/a\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} = - \frac{pdg_{4231}}{pdg_{9139}}\)
LHS diff is pdg1464*(-pdg1939 + pdg9139)/pdg9139 RHS diff is 0 5958392859:
5938459282:
5958392859:
5938459282:
9 square root both sides
  1. 9385938295; locally 2985412:
    \((x+(b/(2 a)))^2 = -(c/a) + (b/(2 a))^2\)
    \(\left(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}}\right)^{2} = \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}\)
  1. 5982958249; locally 6608123:
    \(x+(b/(2 a)) = -\sqrt{(b/(2 a))^2 - (c/a)}\)
    \(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}} = - \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
  2. 9582958294; locally 6608102:
    \(x+(b/(2 a)) = \sqrt{(b/(2 a))^2 - (c/a)}\)
    \(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}} = \sqrt{\frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}}\)
no check performed 9385938295:
5982958249:
9582958294:
9385938295:
5982958249:
9582958294:
8 LHS of expr 1 equals LHS of expr 2
  1. 5928292841; locally 1120000:
    \(x^2 + (b/a)x + (b/(2 a))^2 = -c/a + (b/(2 a))^2\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} + \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} = \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}\)
  2. 5959282914; locally 1734000:
    \(x^2 + x(b/a) + (b/(2 a))^2 = (x+(b/(2 a)))^2\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} + \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} = \left(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}}\right)^{2}\)
  1. 9385938295; locally 2985412:
    \((x+(b/(2 a)))^2 = -(c/a) + (b/(2 a))^2\)
    \(\left(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}}\right)^{2} = \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} - \frac{pdg_{4231}}{pdg_{9139}}\)
input diff is 0 diff is (pdg1464**2*pdg9139 + pdg1464*pdg1939 + pdg4231)/pdg9139 diff is -(pdg1464**2*pdg9139 + pdg1464*pdg1939 + pdg4231)/pdg9139 5928292841:
5959282914:
9385938295:
5928292841:
5959282914:
9385938295:
7 simplify
  1. 5928285821; locally 1239010:
    \(x^2 + 2 x (b/(2 a)) + (b/(2 a))^2 = (x + (b/(2 a)))^2\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} + \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} = \left(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}}\right)^{2}\)
  1. 5959282914; locally 1734000:
    \(x^2 + x(b/a) + (b/(2 a))^2 = (x+(b/(2 a)))^2\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} + \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} = \left(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}}\right)^{2}\)
valid 5928285821:
5959282914:
5928285821:
5959282914:
6 change variable X to Y
  1. 8582954722; locally 9091270:
    \(x^2 + 2 x h + h^2 = (x + h)^2\)
    \(pdg_{1464}^{2} + 2 pdg_{1464} pdg_{3410} + pdg_{3410}^{2} = \left(pdg_{1464} + pdg_{3410}\right)^{2}\)
  1. 0004858592:
    \(h\)
    \(pdg_{3410}\)
  2. 0000999900:
    \(b/(2 a)\)
    \(\frac{pdg_{1939}}{2 pdg_{9139}}\)
  1. 5928285821; locally 1239010:
    \(x^2 + 2 x (b/(2 a)) + (b/(2 a))^2 = (x + (b/(2 a)))^2\)
    \(pdg_{1464}^{2} + \frac{pdg_{1464} pdg_{1939}}{pdg_{9139}} + \frac{pdg_{1939}^{2}}{4 pdg_{9139}^{2}} = \left(pdg_{1464} + \frac{pdg_{1939}}{2 pdg_{9139}}\right)^{2}\)
valid 8582954722: dimensions are consistent
5928285821:
8582954722: N/A
5928285821:
14 declare final expr
  1. 9999999968; locally 8811221:
    \(x = \frac{-b-\sqrt{b^2-4ac}}{2 a}\)
    \(pdg_{1464} = \frac{- pdg_{1939} - \sqrt{pdg_{1939}^{2} - 4 pdg_{4231} pdg_{9139}}}{2 pdg_{9139}}\)
no validation is available for declarations 9999999968:
9999999968:
15 declare final expr
  1. 9999999969; locally 8761200:
    \(x = \frac{-b+\sqrt{b^2-4ac}}{2 a}\)
    \(pdg_{1464} = \frac{- pdg_{1939} + \sqrt{pdg_{1939}^{2} - 4 pdg_{4231} pdg_{9139}}}{2 pdg_{9139}}\)
no validation is available for declarations 9999999969:
9999999969:
3 divide both sides by
  1. 9285928292; locally 8882098:
    \(ax^2 + bx + c = 0\)
    \(pdg_{1464}^{2} pdg_{9139} + pdg_{1464} pdg_{1939} + pdg_{4231} = 0\)
  1. 0002424922:
    \(a\)
    \(pdg_{9139}\)
  1. 5958392859; locally 7777621:
    \(x^2 + (b/a)x+(c/a) = 0\)
    \(pdg_{1464}^{2} + pdg_{1464} + \frac{pdg_{4231}}{pdg_{9139}} = 0\)
LHS diff is pdg1464*(pdg1939 - pdg9139)/pdg9139 RHS diff is 0 9285928292:
5958392859:
9285928292:
5958392859:
1 declare initial expr
  1. 9285928292; locally 8882098:
    \(ax^2 + bx + c = 0\)
    \(pdg_{1464}^{2} pdg_{9139} + pdg_{1464} pdg_{1939} + pdg_{4231} = 0\)
no validation is available for declarations 9285928292:
9285928292:
7.5 declare initial expr
  1. 8582954722; locally 9091270:
    \(x^2 + 2 x h + h^2 = (x + h)^2\)
    \(pdg_{1464}^{2} + 2 pdg_{1464} pdg_{3410} + pdg_{3410}^{2} = \left(pdg_{1464} + pdg_{3410}\right)^{2}\)
no validation is available for declarations 8582954722: dimensions are consistent
 8582954722: N/A
Physics Derivation Graph: Steps for quadratic equation derivation

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
9139 variable a
\(a\)		 ['real'] dimensionless 45
3410 variable h
\(h\)		 real dimensionless none
  • str_note
2
4231 variable c
\(c\)		 ['real'] dimensionless 12
1464 variable x
\(x\)		 ['real'] dimensionless 140
1939 variable b
\(b\)		 ['real'] dimensionless 20
MESSAGE: