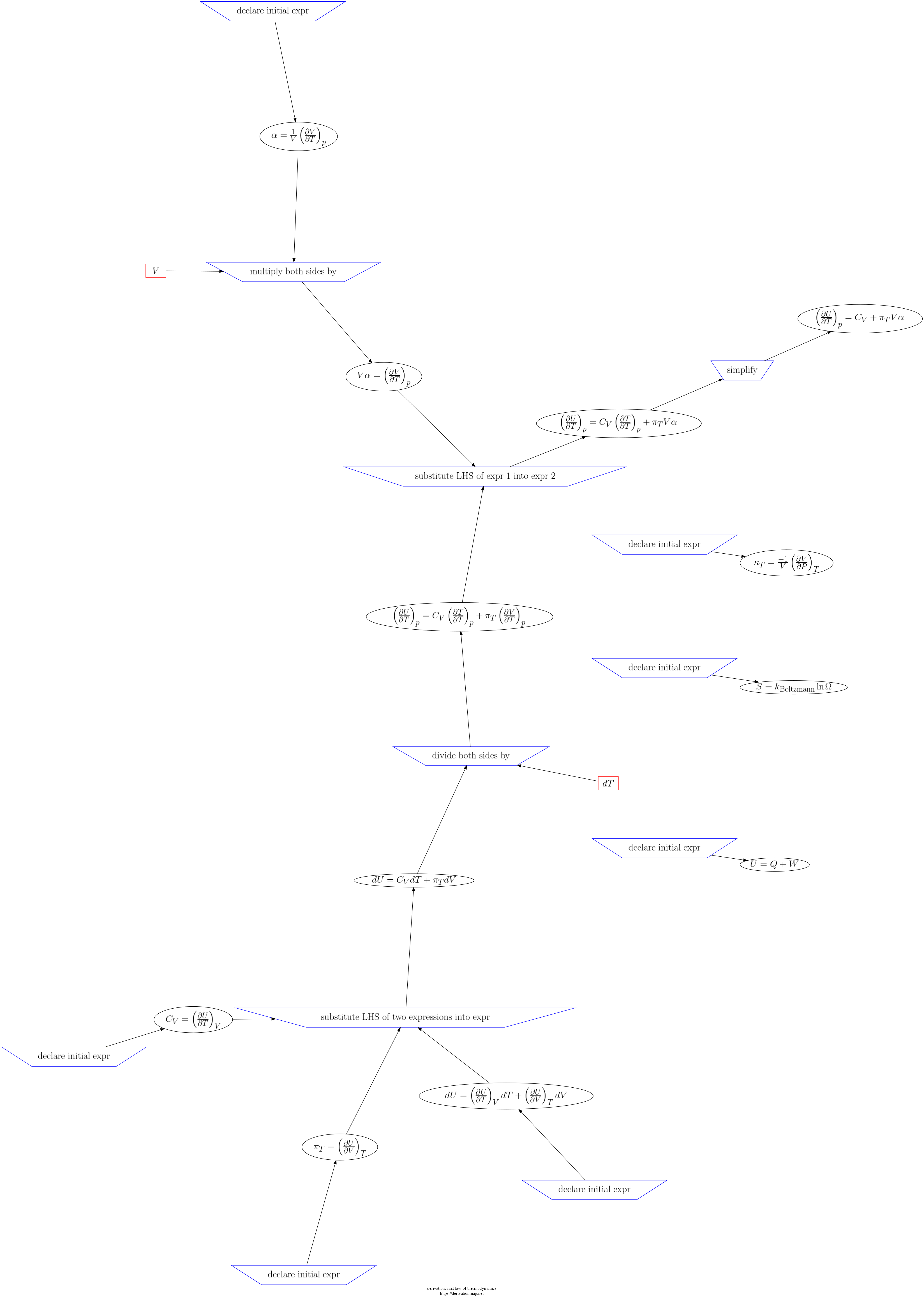
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
https://www.youtube.com/watch?v=QTiqF-HtkS0 and https://www.youtube.com/watch?v=3Yls-t3B49U
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 9 | multiply both sides by |
|
|
|
valid |
3464107376:
6397683463: |
3464107376:
6397683463: |
|
| 6 | substitute LHS of two expressions into expr |
|
|
|
failed |
1085150613:
5634116660: 9941599459: 5002539602: |
1085150613:
5634116660: 9941599459: 5002539602: |
|
| 8 | declare initial expr |
|
|
|
no validation is available for declarations |
3464107376:
|
3464107376:
|
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
1815398659:
|
1815398659:
|
|
| 7 | divide both sides by |
|
|
|
Nothing to split |
5002539602:
6055078815: |
5002539602:
6055078815: |
|
| 11 | simplify |
|
|
|
Nothing to split |
2257410739:
7826132469: |
2257410739:
7826132469: |
|
| 5 | declare initial expr |
|
|
|
no validation is available for declarations |
5634116660:
|
5634116660:
|
|
| 10 | substitute LHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
6397683463:
6055078815: 2257410739: |
6397683463:
6055078815: 2257410739: |
|
| 2 | declare initial expr |
|
|
|
no validation is available for declarations |
9941599459:
|
9941599459:
|
hold volume constant in first term; hold temperature constant in second term |
| 3 | declare initial expr |
|
|
|
no validation is available for declarations |
3547519267:
|
3547519267:
|
|
| 4 | declare initial expr |
|
|
|
no validation is available for declarations |
1085150613:
|
1085150613:
|
|
| 12 | declare initial expr |
|
|
|
no validation is available for declarations |
9781951738:
error for dim with 9781951738 |
9781951738:
N/A |
| symbol ID | category | latex | scope | dimension | name | value | Used in derivations | references | |
|---|---|---|---|---|---|---|---|---|---|
| 6682 | variable |
C_V
\(C_V\) |
real |
|
heat capacity at constant volume | 2 | |||
| 3434 | variable |
\Omega
\(\Omega\) |
real | dimensionless | number of microscopic configurations (known as microstates) that are consistent with the macroscopic quantities that characterize the system | 1 | |||
| 8134 | variable |
P
\(P\) |
real |
|
pressure | 13 | |||
| 5480 | variable |
\pi_T
\(\pi_T\) |
real |
|
internal pressure at constant temperature | 2 | |||
| 1088 | variable |
W
\(W\) |
real |
|
work done to a system | 1 | |||
| 1157 | constant |
k_{Boltzmann}
\(k_{Boltzmann}\) |
['real'] |
|
Boltzmann constant |
1.38064852 10^{-23} meter^2 kilogram second^-2 Kelvin^-1 |
1 | ||
| 1394 | variable |
S
\(S\) |
real |
|
entropy | 1 | |||
| 4645 | variable |
\kappa_T
\(\kappa_T\) |
real | dimensionless | coefficient of isothermal compressibility |
|
6 | ||
| 9432 | variable |
Q
\(Q\) |
real |
|
heat flow | 1 | |||
| 4686 | variable |
\alpha
\(\alpha\) |
real |
|
expansion coefficient | 6 | |||
| 7586 | variable |
V
\(V\) |
real |
|
volume | 15 | |||
| 7343 | variable |
T
\(T\) |
real |
|
temperature | 18 | |||
| 5786 | variable |
U
\(U\) |
real |
|
internal energy | 7 |