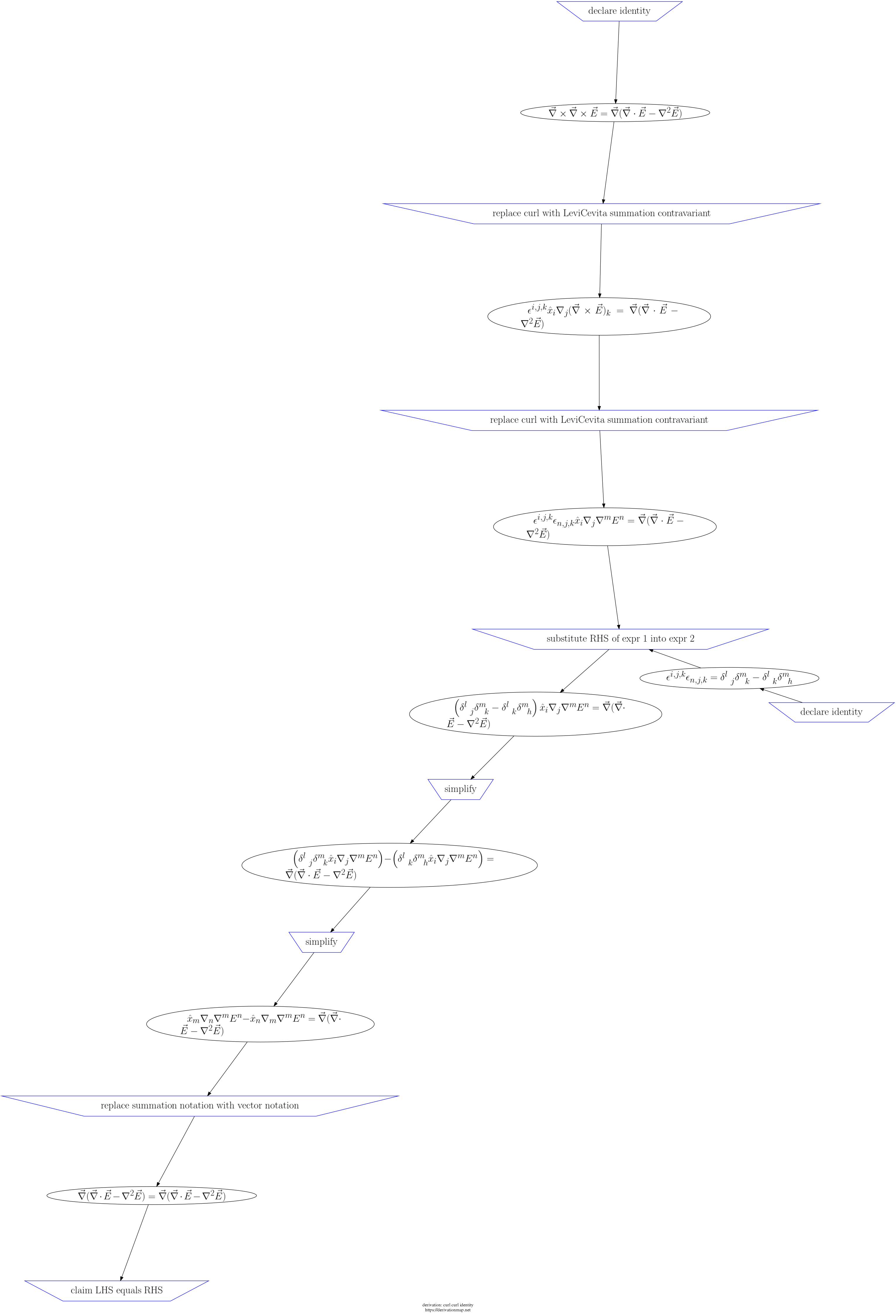
Physics Derivation Graph navigation Sign in

review derivation: curl curl identity

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
8 replace summation notation with vector notation
  1. 7575859310; locally 3948472:
    \(\hat{x}_m \nabla_n \nabla^m E^n - \hat{x}_n \nabla_m \nabla^m E^n = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
  1. 7575859312; locally 2109231:
    \(\vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E}) = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
Nothing to split 7575859310:
7575859312:
7575859310:
7575859312:
2 replace curl with LeviCevita summation contravariant
  1. 7575859295; locally 1939485:
    \(\vec{ \nabla} \times \vec{ \nabla} \times \vec{E} = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
  1. 7575859300; locally 9485482:
    \(\epsilon^{i,j,k} \hat{x}_i \nabla_j ( \vec{ \nabla} \times \vec{E} )_k = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
Nothing to split 7575859295:
7575859300:
7575859295:
7575859300:
5 substitute RHS of expr 1 into expr 2
  1. 7575859304; locally 2934842:
    \(\epsilon^{i,j,k} \epsilon_{n,j,k} = \delta^{l}_{\ \ j} \delta^{m}_{\ \ k} - \delta^{l}_{\ \ k} \delta^{m}_{\ \ h}\)
    \(\)
  2. 7575859302; locally 2941319:
    \(\epsilon^{i,j,k} \epsilon_{n,j,k} \hat{x}_i \nabla_j \nabla^m E^n = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
  1. 7575859306; locally 3949292:
    \(\left( \delta^{l}_{\ \ j} \delta^{m}_{\ \ k} - \delta^{l}_{\ \ k} \delta^{m}_{\ \ h} \right) \hat{x}_i \nabla_j \nabla^m E^n = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
failed 7575859304: failed
7575859302:
7575859306:
7575859304: N/A
7575859302:
7575859306:
7 simplify
  1. 7575859308; locally 3844221:
    \(\left( \delta^{l}_{\ \ j} \delta^{m}_{\ \ k} \hat{x}_i \nabla_j \nabla^m E^n\right)-\left( \delta^{l}_{\ \ k} \delta^{m}_{\ \ h} \hat{x}_i \nabla_j \nabla^m E^n \right) = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
  1. 7575859310; locally 3948472:
    \(\hat{x}_m \nabla_n \nabla^m E^n - \hat{x}_n \nabla_m \nabla^m E^n = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
Nothing to split 7575859308:
7575859310:
7575859308:
7575859310:
6 simplify
  1. 7575859306; locally 3949292:
    \(\left( \delta^{l}_{\ \ j} \delta^{m}_{\ \ k} - \delta^{l}_{\ \ k} \delta^{m}_{\ \ h} \right) \hat{x}_i \nabla_j \nabla^m E^n = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
  1. 7575859308; locally 3844221:
    \(\left( \delta^{l}_{\ \ j} \delta^{m}_{\ \ k} \hat{x}_i \nabla_j \nabla^m E^n\right)-\left( \delta^{l}_{\ \ k} \delta^{m}_{\ \ h} \hat{x}_i \nabla_j \nabla^m E^n \right) = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
failed 7575859306:
7575859308:
7575859306:
7575859308:
3 replace curl with LeviCevita summation contravariant
  1. 7575859300; locally 9485482:
    \(\epsilon^{i,j,k} \hat{x}_i \nabla_j ( \vec{ \nabla} \times \vec{E} )_k = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
  1. 7575859302; locally 2941319:
    \(\epsilon^{i,j,k} \epsilon_{n,j,k} \hat{x}_i \nabla_j \nabla^m E^n = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
Nothing to split 7575859300:
7575859302:
7575859300:
7575859302:
1 declare identity
  1. 7575859295; locally 1939485:
    \(\vec{ \nabla} \times \vec{ \nabla} \times \vec{E} = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
no validation is available for declarations 7575859295:
7575859295:
9 claim LHS equals RHS
  1. 7575859312; locally 2109231:
    \(\vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E}) = \vec{ \nabla}( \vec{ \nabla} \cdot \vec{E} - \nabla^2 \vec{E})\)
    \(\)
Nothing to split 7575859312:
7575859312:
4 declare identity
  1. 7575859304; locally 2934842:
    \(\epsilon^{i,j,k} \epsilon_{n,j,k} = \delta^{l}_{\ \ j} \delta^{m}_{\ \ k} - \delta^{l}_{\ \ k} \delta^{m}_{\ \ h}\)
    \(\)
no validation is available for declarations 7575859304: failed
 7575859304: N/A
Physics Derivation Graph: Steps for curl curl identity

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
7930 variable m
\(m\)		 integer dimensionless index
  • str_note
5
1434 variable \hat{x}_n
\(\hat{x}_n\)		 real dimensionless nth unit vector
  • str_note
1
1552 variable j
\(j\)		 ['integer'] dimensionless index 7
2380 variable \hat{x}_m
\(\hat{x}_m\)		 real dimensionless mth unit vector
  • str_note
1
9690 variable k
\(k\)		 integer dimensionless index
  • str_note
4
8349 variable \hat{x}_i
\(\hat{x}_i\)		 real dimensionless ith unit vector
  • str_note
3
1567 variable i
\(i\)		 ['integer'] dimensionless index 1
1592 variable n
\(n\)		 integer dimensionless index 23
6238 variable E
\(E\)		 real dimensionless electric field 20
8304 variable l
\(l\)		 integer dimensionless index
  • str_note
3
7984 variable i
\(i\)		 integer dimensionless index
  • str_note
1
4326 variable \vec{E}
\(\vec{E}\)		 complex dimensionless electric field 9
MESSAGES: