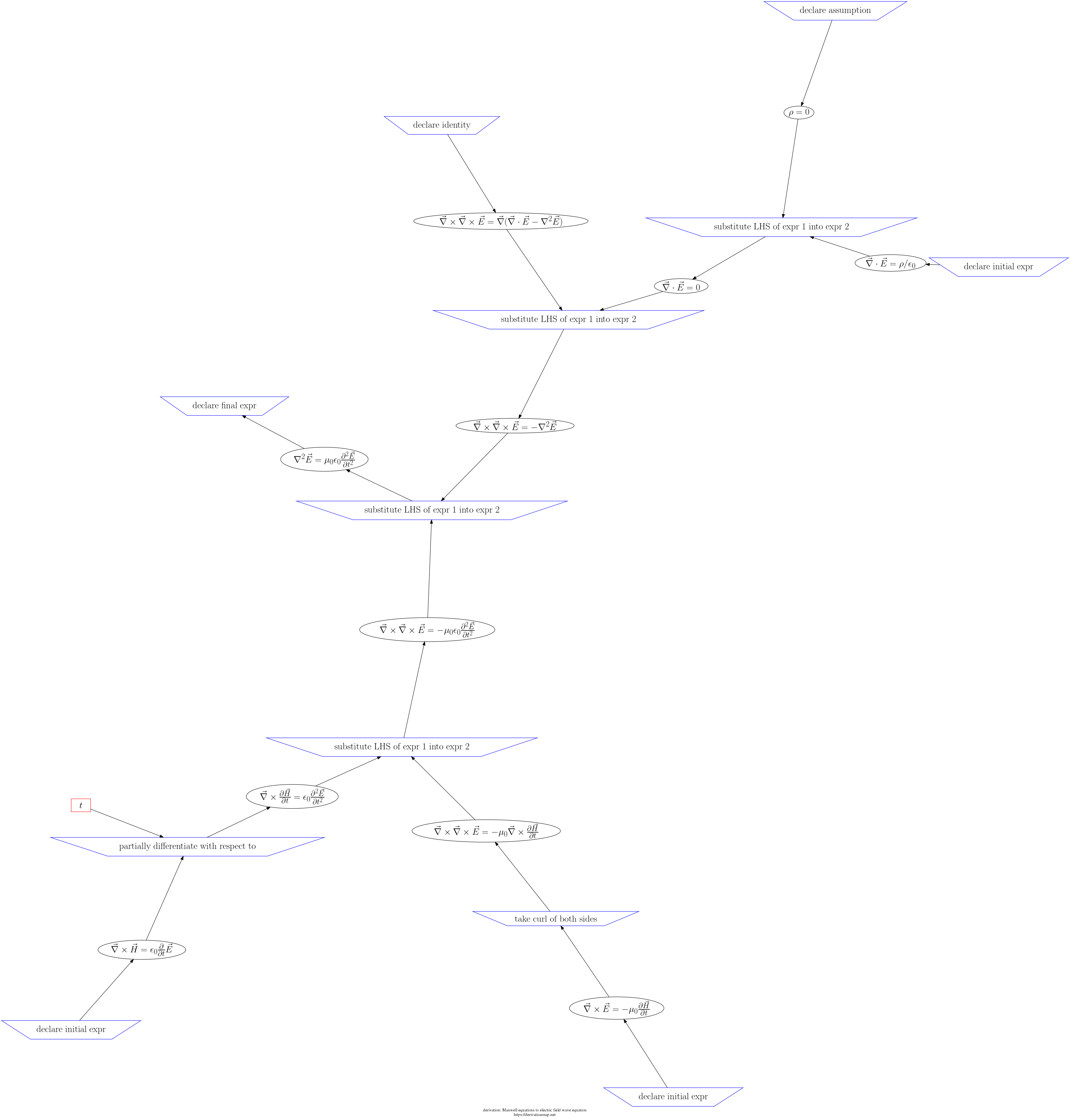
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 3 | partially differentiate with respect to |
|
|
|
Nothing to split |
1314864131:
1314464131: |
1314864131:
1314464131: |
|
| 5 | substitute LHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
9291999979:
1314464131: 3947269979: |
9291999979:
1314464131: 3947269979: |
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
9991999979:
|
9991999979:
|
|
| 1.3 | declare initial expr |
|
|
|
no validation is available for declarations |
1314864131:
|
1314864131:
|
|
| 1.6 | declare initial expr |
|
|
|
no validation is available for declarations |
9999999981:
failed |
9999999981:
N/A |
|
| 11 | substitute LHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
1636453295:
3947269979: 8494839423: |
1636453295:
3947269979: 8494839423: |
|
| 7 | declare assumption |
|
|
|
no validation is available for declarations |
9919999981:
inconsistent dimensions |
9919999981:
N/A |
|
| 9 | declare identity |
|
|
|
no validation is available for declarations |
7575859295:
|
7575859295:
|
|
| 12 | declare final expr |
|
|
|
no validation is available for declarations |
8494839423:
|
8494839423:
|
|
| 4 | take curl of both sides |
|
|
|
no check performed |
9991999979:
9291999979: |
9991999979:
9291999979: |
|
| 10 | substitute LHS of expr 1 into expr 2 |
|
|
|
failed |
7575859295:
7466829492: error for dim with 7466829492 1636453295: |
7575859295:
7466829492: N/A 1636453295: |
|
| 8 | substitute LHS of expr 1 into expr 2 |
|
|
|
LHS diff is pdg3935 - Dot(nabla, pdg6238) RHS diff is 0 |
9999999981:
failed 9919999981: inconsistent dimensions 7466829492: error for dim with 7466829492 |
9999999981:
N/A 9919999981: N/A 7466829492: N/A |
| symbol ID | category | latex | scope | dimension | name | value | Used in derivations | references | |
|---|---|---|---|---|---|---|---|---|---|
| 1467 | variable |
t
\(t\) |
['real'] |
|
time |
|
121 | ||
| 4326 | variable |
\vec{E}
\(\vec{E}\) |
complex | dimensionless | electric field | 9 | |||
| 7940 | constant |
\epsilon_0
\(\epsilon_0\) |
real |
|
vacuum permittivity, permittivity of free space or electric constant or the distributed capacitance of the vacuum |
8.8541878128E-{12} F/m |
14 | ||
| 6197 | constant |
\mu_0
\(\mu_0\) |
real |
|
vacuum permeability, permeability of free space, permeability of vacuum, or magnetic constant |
1.25663706212E^{-6} N/A^2 |
8 | ||
| 3935 | variable |
\rho
\(\rho\) |
real |
|
density | 7 | |||
| 2069 | variable |
\vec{H}
\(\vec{H}\) |
real | dimensionless | magnetic field | 3 | |||
| 6238 | variable |
E
\(E\) |
real | dimensionless | electric field | 20 |