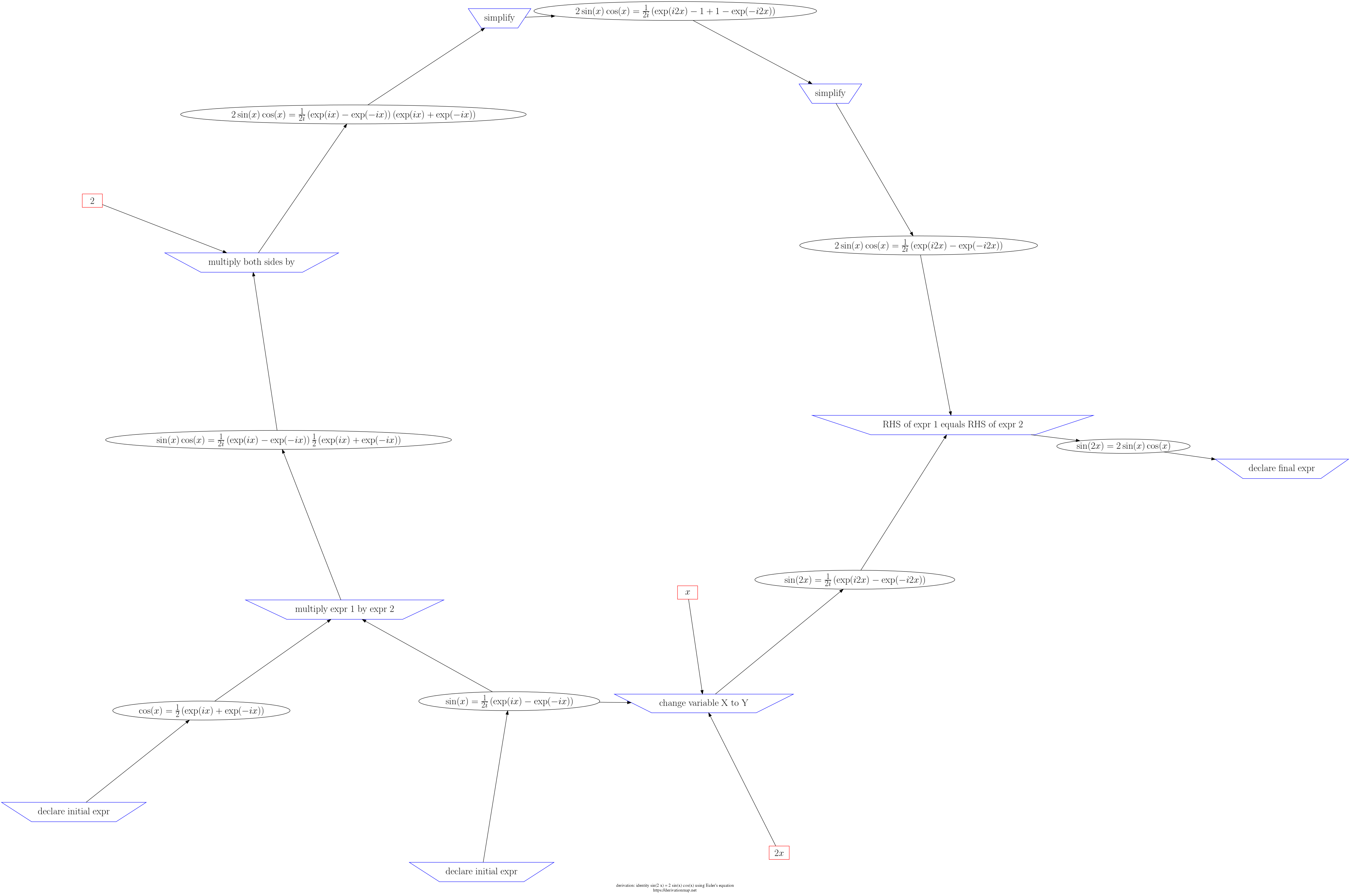
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
| Index |
Inference Rule |
Input latex |
Feeds latex |
Output latex |
step validity |
dimension check |
unit check |
notes |
|
4
|
multiply expr 1 by expr 2 |
-
2103023049; locally 6060683:
\(\sin(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)\)
\(\sin{\left(pdg_{1464} \right)} = \frac{e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
-
4585932229; locally 5011637:
\(\cos(x) = \frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)\)
\(\cos{\left(pdg_{1464} \right)} = \frac{e^{pdg_{1464} pdg_{4621}}}{2} + \frac{e^{- pdg_{1464} pdg_{4621}}}{2}\)
|
|
-
3470587782; locally 6350246:
\(\sin(x) \cos(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right) \frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)\)
\(\sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{\left(\frac{e^{pdg_{1464} pdg_{4621}}}{2} + \frac{e^{- pdg_{1464} pdg_{4621}}}{2}\right) \left(e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}\right)}{2 pdg_{4621}}\)
|
valid |
2103023049:
4585932229:
3470587782:
|
2103023049:
4585932229:
3470587782:
|
|
|
8
|
RHS of expr 1 equals RHS of expr 2 |
-
9180861128; locally 6229292:
\(2 \sin(x) \cos(x) = \frac{1}{2 i} \left( \exp(i 2 x) - \exp(-i 2 x) \right)\)
\(2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{e^{2 pdg_{1464} pdg_{4621}} - e^{- 2 pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
-
8483686863; locally 1414263:
\(\sin(2 x) = \frac{1}{2i}\left(\exp(i 2 x)-\exp(-i 2 x) \right)\)
\(\sin{\left(2 pdg_{1464} \right)} = \frac{e^{2 pdg_{1464} pdg_{4621}} - e^{- 2 pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
|
-
2405307372; locally 7647794:
\(\sin(2 x) = 2 \sin(x) \cos(x)\)
\(\sin{\left(2 pdg_{1464} \right)} = 2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)}\)
|
valid |
9180861128:
8483686863:
2405307372:
|
9180861128:
8483686863:
2405307372:
|
|
|
1
|
declare initial expr |
|
|
-
2103023049; locally 6060683:
\(\sin(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)\)
\(\sin{\left(pdg_{1464} \right)} = \frac{e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
no validation is available for declarations |
2103023049:
|
2103023049:
|
|
|
3
|
declare initial expr |
|
|
-
4585932229; locally 5011637:
\(\cos(x) = \frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)\)
\(\cos{\left(pdg_{1464} \right)} = \frac{e^{pdg_{1464} pdg_{4621}}}{2} + \frac{e^{- pdg_{1464} pdg_{4621}}}{2}\)
|
no validation is available for declarations |
4585932229:
|
4585932229:
|
|
|
2
|
change variable X to Y |
-
2103023049; locally 6060683:
\(\sin(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)\)
\(\sin{\left(pdg_{1464} \right)} = \frac{e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
-
4961662865:
\(x\)
\(pdg_{1464}\)
-
9110536742:
\(2 x\)
\(2 pdg_{1464}\)
|
-
8483686863; locally 1414263:
\(\sin(2 x) = \frac{1}{2i}\left(\exp(i 2 x)-\exp(-i 2 x) \right)\)
\(\sin{\left(2 pdg_{1464} \right)} = \frac{e^{2 pdg_{1464} pdg_{4621}} - e^{- 2 pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
valid |
2103023049:
8483686863:
|
2103023049:
8483686863:
|
|
|
7
|
simplify |
-
8699789241; locally 5714636:
\(2 \sin(x) \cos(x) = \frac{1}{2 i} \left( \exp(i 2 x) - 1 + 1 - \exp(-i 2 x) \right)\)
\(2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{e^{2 pdg_{1464} pdg_{4621}} - e^{- 2 pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
|
-
9180861128; locally 6229292:
\(2 \sin(x) \cos(x) = \frac{1}{2 i} \left( \exp(i 2 x) - \exp(-i 2 x) \right)\)
\(2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{e^{2 pdg_{1464} pdg_{4621}} - e^{- 2 pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
valid |
8699789241:
error for dim with 8699789241
9180861128:
|
8699789241:
N/A
9180861128:
|
|
|
9
|
declare final expr |
-
2405307372; locally 7647794:
\(\sin(2 x) = 2 \sin(x) \cos(x)\)
\(\sin{\left(2 pdg_{1464} \right)} = 2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)}\)
|
|
|
no validation is available for declarations |
2405307372:
|
2405307372:
|
|
|
5
|
multiply both sides by |
-
3470587782; locally 6350246:
\(\sin(x) \cos(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right) \frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)\)
\(\sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{\left(\frac{e^{pdg_{1464} pdg_{4621}}}{2} + \frac{e^{- pdg_{1464} pdg_{4621}}}{2}\right) \left(e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}\right)}{2 pdg_{4621}}\)
|
-
8642992037:
\(2\)
\(2\)
|
-
9894826550; locally 7867574:
\(2 \sin(x) \cos(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right) \left(\exp(i x)+\exp(-i x) \right)\)
\(2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{\left(e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}\right) \left(e^{pdg_{1464} pdg_{4621}} + e^{- pdg_{1464} pdg_{4621}}\right)}{2 pdg_{4621}}\)
|
valid |
3470587782:
9894826550:
error for dim with 9894826550
|
3470587782:
9894826550:
N/A
|
|
|
6
|
simplify |
-
9894826550; locally 7867574:
\(2 \sin(x) \cos(x) = \frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right) \left(\exp(i x)+\exp(-i x) \right)\)
\(2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{\left(e^{pdg_{1464} pdg_{4621}} - e^{- pdg_{1464} pdg_{4621}}\right) \left(e^{pdg_{1464} pdg_{4621}} + e^{- pdg_{1464} pdg_{4621}}\right)}{2 pdg_{4621}}\)
|
|
-
8699789241; locally 5714636:
\(2 \sin(x) \cos(x) = \frac{1}{2 i} \left( \exp(i 2 x) - 1 + 1 - \exp(-i 2 x) \right)\)
\(2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)} = \frac{e^{2 pdg_{1464} pdg_{4621}} - e^{- 2 pdg_{1464} pdg_{4621}}}{2 pdg_{4621}}\)
|
valid |
9894826550:
error for dim with 9894826550
8699789241:
error for dim with 8699789241
|
9894826550:
N/A
8699789241:
N/A
|
|
Physics Derivation Graph: Steps for identity sin(2 x) = 2 sin(x) cos(x) using Euler's equation
Clicking on the step index will take you to the page where you can edit that step.