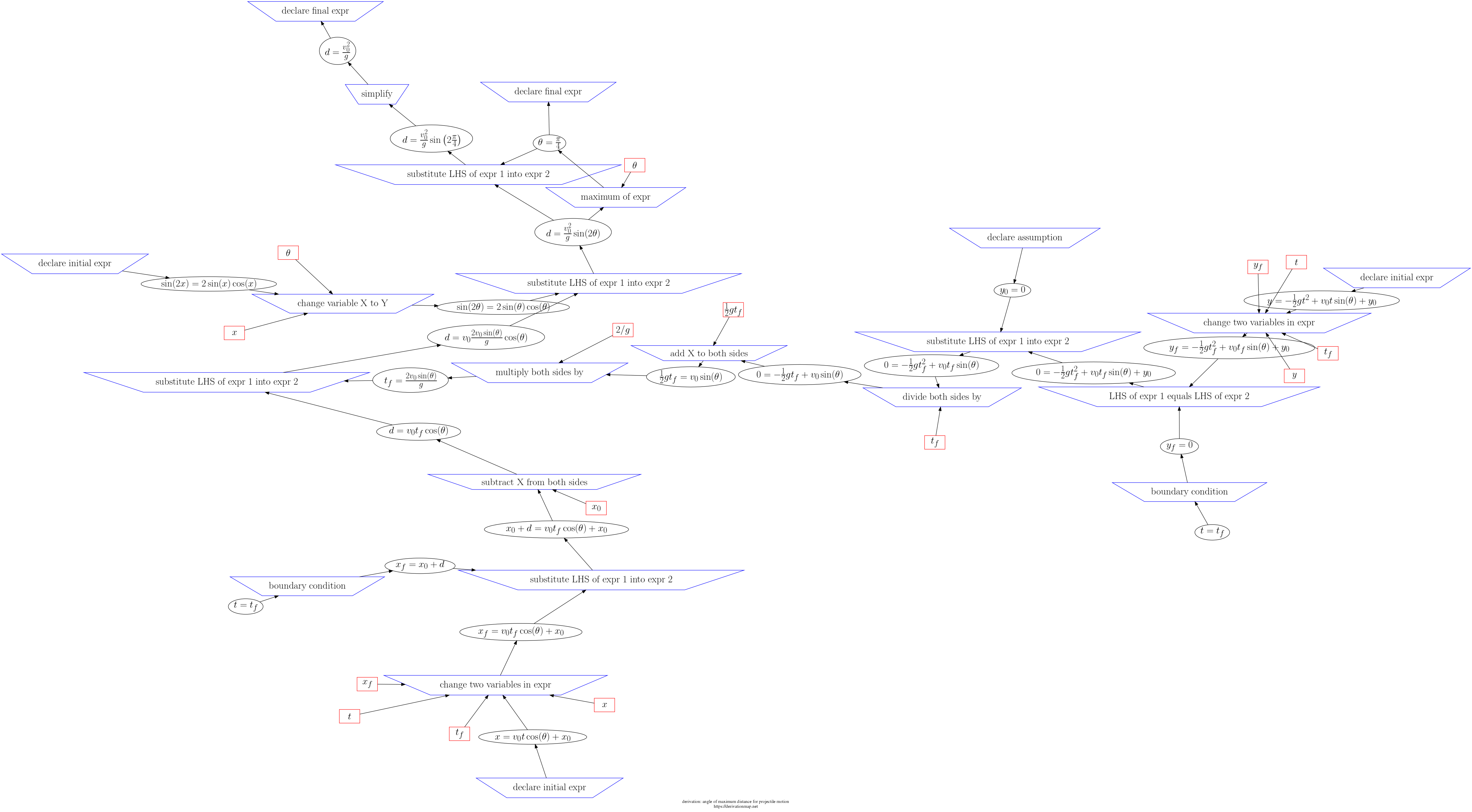
Physics Derivation Graph navigation Sign in

review derivation: angle of maximum distance for projectile motion

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
7 divide both sides by
  1. 1087417579; locally 7465542:
    \(0 = - \frac{1}{2} g t_f^2 + v_0 t_f \sin(\theta)\)
    \(0 = - \frac{pdg_{1649} pdg_{2467}^{2}}{2} + pdg_{2467} pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
  1. 4829590294:
    \(t_f\)
    \(pdg_{2467}\)
  1. 2086924031; locally 5115586:
    \(0 = - \frac{1}{2} g t_f + v_0 \sin(\theta)\)
    \(0 = - \frac{pdg_{1649} pdg_{2467}}{2} + pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
valid 1087417579:
2086924031:
1087417579:
2086924031:
4 LHS of expr 1 equals LHS of expr 2
  1. 5379546684; locally 8592617:
    \(y_f = - \frac{1}{2} g t_f^2 + v_0 t_f \sin(\theta) + y_0\)
    \(pdg_{7092} = pdg_{1469} - \frac{pdg_{1649} pdg_{2467}^{2}}{2} + pdg_{2467} pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
  2. 9112191201; locally 4911015:
    \(y_f = 0\)
    \(pdg_{7092} = 0\)
  1. 8198310977; locally 7336772:
    \(0 = - \frac{1}{2} g t_f^2 + v_0 t_f \sin(\theta) + y_0\)
    \(0 = pdg_{1469} - \frac{pdg_{1649} pdg_{2467}^{2}}{2} + pdg_{2467} pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
input diff is 0 diff is -pdg1469 + pdg1649*pdg2467**2/2 - pdg2467*pdg5153*sin(pdg1575) diff is pdg1469 - pdg1649*pdg2467**2/2 + pdg2467*pdg5153*sin(pdg1575) 5379546684:
9112191201:
8198310977:
5379546684:
9112191201:
8198310977:
22 declare final expr
  1. 5353282496; locally 6972103:
    \(d = \frac{v_0^2}{g}\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2}}{pdg_{1649}}\)
no validation is available for declarations 5353282496:
5353282496:
16 declare initial expr
  1. 2405307372; locally 6199255:
    \(\sin(2 x) = 2 \sin(x) \cos(x)\)
    \(\sin{\left(2 pdg_{1464} \right)} = 2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)}\)
no validation is available for declarations 2405307372:
2405307372:
10 declare initial expr
  1. 5438722682; locally 2022953:
    \(x = v_0 t \cos(\theta) + x_0\)
    \(pdg_{4037} = pdg_{1467} pdg_{5153} \cos{\left(pdg_{1575} \right)} + pdg_{1572}\)
no validation is available for declarations 5438722682:
5438722682:
21 simplify
  1. 3607070319; locally 9834994:
    \(d = \frac{v_0^2}{g} \sin\left(2 \frac{\pi}{4}\right)\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2} \sin{\left(\frac{pdg_{3141}}{2} \right)}}{pdg_{1649}}\)
  1. 5353282496; locally 6972103:
    \(d = \frac{v_0^2}{g}\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2}}{pdg_{1649}}\)
LHS diff is 0 RHS diff is pdg5153**2*(sin(pdg3141/2) - 1)/pdg1649 3607070319:
5353282496:
3607070319:
5353282496:
12 boundary condition
  1. 4370074654; locally 1654988:
    \(t = t_f\)
    \(pdg_{1467} = pdg_{2467}\)
  1. 2378095808; locally 5891715:
    \(x_f = x_0 + d\)
    \(pdg_{3652} = pdg_{1572} + pdg_{1943}\)
no validation is available for assumptions 4370074654:
2378095808:
4370074654:
2378095808:
13 substitute LHS of expr 1 into expr 2
  1. 2378095808; locally 5891715:
    \(x_f = x_0 + d\)
    \(pdg_{3652} = pdg_{1572} + pdg_{1943}\)
  2. 3485125659; locally 2293278:
    \(x_f = v_0 t_f \cos(\theta) + x_0\)
    \(pdg_{3652} = pdg_{1572} + pdg_{2467} pdg_{5153} \cos{\left(pdg_{1575} \right)}\)
  1. 4268085801; locally 6742208:
    \(x_0 + d = v_0 t_f \cos(\theta) + x_0\)
    \(pdg_{1572} + pdg_{1943} = pdg_{1572} + pdg_{2467} pdg_{5153} \cos{\left(pdg_{1575} \right)}\)
valid 2378095808:
3485125659:
4268085801:
2378095808:
3485125659:
4268085801:
14 subtract X from both sides
  1. 4268085801; locally 6742208:
    \(x_0 + d = v_0 t_f \cos(\theta) + x_0\)
    \(pdg_{1572} + pdg_{1943} = pdg_{1572} + pdg_{2467} pdg_{5153} \cos{\left(pdg_{1575} \right)}\)
  1. 8072682558:
    \(x_0\)
    \(pdg_{1572}\)
  1. 7233558441; locally 6756414:
    \(d = v_0 t_f \cos(\theta)\)
    \(pdg_{1943} = pdg_{2467} pdg_{5153} \cos{\left(pdg_{1575} \right)}\)
valid 4268085801:
7233558441:
4268085801:
7233558441:
11 change two variables in expr
  1. 5438722682; locally 2022953:
    \(x = v_0 t \cos(\theta) + x_0\)
    \(pdg_{4037} = pdg_{1467} pdg_{5153} \cos{\left(pdg_{1575} \right)} + pdg_{1572}\)
  1. 3273630811:
    \(x\)
    \(pdg_{4037}\)
  2. 5194141542:
    \(x_f\)
    \(pdg_{3652}\)
  3. 6732786762:
    \(t\)
    \(pdg_{1467}\)
  4. 6463266449:
    \(t_f\)
    \(pdg_{2467}\)
  1. 3485125659; locally 2293278:
    \(x_f = v_0 t_f \cos(\theta) + x_0\)
    \(pdg_{3652} = pdg_{1572} + pdg_{2467} pdg_{5153} \cos{\left(pdg_{1575} \right)}\)
valid 5438722682:
3485125659:
5438722682:
3485125659:
2 change two variables in expr
  1. 9862900242; locally 1292901:
    \(y = - \frac{1}{2} g t^2 + v_0 t \sin(\theta) + y_0\)
    \(pdg_{5647} = - \frac{pdg_{1467}^{2} pdg_{1649}}{2} + pdg_{1467} pdg_{5153} \sin{\left(pdg_{1575} \right)} + pdg_{1469}\)
  1. 8406170337:
    \(y\)
    \(pdg_{5647}\)
  2. 8120663858:
    \(y_f\)
    \(pdg_{7092}\)
  3. 2403773761:
    \(t\)
    \(pdg_{1467}\)
  4. 4162188238:
    \(t_f\)
    \(pdg_{2467}\)
  1. 5379546684; locally 8592617:
    \(y_f = - \frac{1}{2} g t_f^2 + v_0 t_f \sin(\theta) + y_0\)
    \(pdg_{7092} = pdg_{1469} - \frac{pdg_{1649} pdg_{2467}^{2}}{2} + pdg_{2467} pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
valid 9862900242:
5379546684:
9862900242:
5379546684:
6 substitute LHS of expr 1 into expr 2
  1. 8198310977; locally 7336772:
    \(0 = - \frac{1}{2} g t_f^2 + v_0 t_f \sin(\theta) + y_0\)
    \(0 = pdg_{1469} - \frac{pdg_{1649} pdg_{2467}^{2}}{2} + pdg_{2467} pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
  2. 1650441634; locally 2601896:
    \(y_0 = 0\)
    \(pdg_{1469} = 0\)
  1. 1087417579; locally 7465542:
    \(0 = - \frac{1}{2} g t_f^2 + v_0 t_f \sin(\theta)\)
    \(0 = - \frac{pdg_{1649} pdg_{2467}^{2}}{2} + pdg_{2467} pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
LHS diff is pdg1469 RHS diff is pdg1469 8198310977:
1650441634:
1087417579:
8198310977:
1650441634:
1087417579:
18 substitute LHS of expr 1 into expr 2
  1. 2519058903; locally 7596368:
    \(\sin(2 \theta) = 2 \sin(\theta) \cos(\theta)\)
    \(\sin{\left(2 pdg_{1575} \right)} = 2 \sin{\left(pdg_{1575} \right)} \cos{\left(pdg_{1575} \right)}\)
  2. 2297105551; locally 4362314:
    \(d = v_0 \frac{2 v_0 \sin(\theta)}{g} \cos(\theta)\)
    \(pdg_{1943} = \frac{2 pdg_{5153}^{2} \sin{\left(pdg_{1575} \right)} \cos{\left(pdg_{1575} \right)}}{pdg_{1649}}\)
  1. 8922441655; locally 5129639:
    \(d = \frac{v_0^2}{g} \sin(2 \theta)\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2} \sin{\left(2 pdg_{1575} \right)}}{pdg_{1649}}\)
valid 2519058903:
2297105551:
8922441655: error for dim with 8922441655
 2519058903:
2297105551:
8922441655: N/A
3 boundary condition
  1. 5373931751; locally 7946350:
    \(t = t_f\)
    \(pdg_{1467} = pdg_{2467}\)
  1. 9112191201; locally 4911015:
    \(y_f = 0\)
    \(pdg_{7092} = 0\)
no validation is available for assumptions 5373931751:
9112191201:
5373931751:
9112191201:
y(t_f) = y_f = 0
23 declare final expr
  1. 1541916015; locally 2728170:
    \(\theta = \frac{\pi}{4}\)
    \(pdg_{1575} = \frac{pdg_{3141}}{4}\)
no validation is available for declarations 1541916015: dimensions are consistent
 1541916015: N/A
9 multiply both sides by
  1. 1191796961; locally 3904454:
    \(\frac{1}{2} g t_f = v_0 \sin(\theta)\)
    \(\frac{pdg_{1649} pdg_{2467}}{2} = pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
  1. 2510804451:
    \(2/g\)
    \(\frac{2}{pdg_{1649}}\)
  1. 4778077984; locally 8982886:
    \(t_f = \frac{2 v_0 \sin(\theta)}{g}\)
    \(pdg_{2467} = \frac{2 pdg_{5153} \sin{\left(pdg_{1575} \right)}}{pdg_{1649}}\)
valid 1191796961:
4778077984:
1191796961:
4778077984:
15 substitute LHS of expr 1 into expr 2
  1. 4778077984; locally 8982886:
    \(t_f = \frac{2 v_0 \sin(\theta)}{g}\)
    \(pdg_{2467} = \frac{2 pdg_{5153} \sin{\left(pdg_{1575} \right)}}{pdg_{1649}}\)
  2. 7233558441; locally 6756414:
    \(d = v_0 t_f \cos(\theta)\)
    \(pdg_{1943} = pdg_{2467} pdg_{5153} \cos{\left(pdg_{1575} \right)}\)
  1. 2297105551; locally 4362314:
    \(d = v_0 \frac{2 v_0 \sin(\theta)}{g} \cos(\theta)\)
    \(pdg_{1943} = \frac{2 pdg_{5153}^{2} \sin{\left(pdg_{1575} \right)} \cos{\left(pdg_{1575} \right)}}{pdg_{1649}}\)
valid 4778077984:
7233558441:
2297105551:
4778077984:
7233558441:
2297105551:
1 declare initial expr
  1. 9862900242; locally 1292901:
    \(y = - \frac{1}{2} g t^2 + v_0 t \sin(\theta) + y_0\)
    \(pdg_{5647} = - \frac{pdg_{1467}^{2} pdg_{1649}}{2} + pdg_{1467} pdg_{5153} \sin{\left(pdg_{1575} \right)} + pdg_{1469}\)
no validation is available for declarations 9862900242:
9862900242:
8 add X to both sides
  1. 2086924031; locally 5115586:
    \(0 = - \frac{1}{2} g t_f + v_0 \sin(\theta)\)
    \(0 = - \frac{pdg_{1649} pdg_{2467}}{2} + pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
  1. 6974054946:
    \(\frac{1}{2} g t_f\)
    \(\frac{pdg_{1649} pdg_{2467}}{2}\)
  1. 1191796961; locally 3904454:
    \(\frac{1}{2} g t_f = v_0 \sin(\theta)\)
    \(\frac{pdg_{1649} pdg_{2467}}{2} = pdg_{5153} \sin{\left(pdg_{1575} \right)}\)
valid 2086924031:
1191796961:
2086924031:
1191796961:
20 substitute LHS of expr 1 into expr 2
  1. 1541916015; locally 2728170:
    \(\theta = \frac{\pi}{4}\)
    \(pdg_{1575} = \frac{pdg_{3141}}{4}\)
  2. 8922441655; locally 5129639:
    \(d = \frac{v_0^2}{g} \sin(2 \theta)\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2} \sin{\left(2 pdg_{1575} \right)}}{pdg_{1649}}\)
  1. 3607070319; locally 9834994:
    \(d = \frac{v_0^2}{g} \sin\left(2 \frac{\pi}{4}\right)\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2} \sin{\left(\frac{pdg_{3141}}{2} \right)}}{pdg_{1649}}\)
valid 1541916015: dimensions are consistent
8922441655: error for dim with 8922441655
3607070319:
1541916015: N/A
8922441655: N/A
3607070319:
5 declare assumption
  1. 1650441634; locally 2601896:
    \(y_0 = 0\)
    \(pdg_{1469} = 0\)
no validation is available for declarations 1650441634:
1650441634:
17 change variable X to Y
  1. 2405307372; locally 6199255:
    \(\sin(2 x) = 2 \sin(x) \cos(x)\)
    \(\sin{\left(2 pdg_{1464} \right)} = 2 \sin{\left(pdg_{1464} \right)} \cos{\left(pdg_{1464} \right)}\)
  1. 7587034465:
    \(\theta\)
    \(pdg_{1575}\)
  2. 7214442790:
    \(x\)
    \(pdg_{1464}\)
  1. 2519058903; locally 7596368:
    \(\sin(2 \theta) = 2 \sin(\theta) \cos(\theta)\)
    \(\sin{\left(2 pdg_{1575} \right)} = 2 \sin{\left(pdg_{1575} \right)} \cos{\left(pdg_{1575} \right)}\)
LHS diff is sin(2*pdg1464) - sin(2*pdg1575) RHS diff is sin(2*pdg1464) - sin(2*pdg1575) 2405307372:
2519058903:
2405307372:
2519058903:
19 maximum of expr
  1. 8922441655; locally 5129639:
    \(d = \frac{v_0^2}{g} \sin(2 \theta)\)
    \(pdg_{1943} = \frac{pdg_{5153}^{2} \sin{\left(2 pdg_{1575} \right)}}{pdg_{1649}}\)
  1. 5667870149:
    \(\theta\)
    \(pdg_{1575}\)
  1. 1541916015; locally 2728170:
    \(\theta = \frac{\pi}{4}\)
    \(pdg_{1575} = \frac{pdg_{3141}}{4}\)
no check performed 8922441655: error for dim with 8922441655
1541916015: dimensions are consistent
 8922441655: N/A
1541916015: N/A
Physics Derivation Graph: Steps for angle of maximum distance for projectile motion

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
1649 variable g
\(g\)		 ['real']
  • length: 1
  • time: -2
 acceleration due to gravity 27
7092 variable y_f
\(y_f\)		 ['real']
  • length: 1
 final position on y axis 3
1469 variable y_0
\(y_0\)		 ['real']
  • length: 1
 initial position 9
5153 variable v_0
\(v_0\)		 ['real']
  • length: 1
  • time: -1
 initial velocity 44
1943 variable d
\(d\)		 ['real']
  • length: 1
 displacement 25
2467 variable t_f
\(t_f\)		 ['real']
  • time: 1
 final time 15
1467 variable t
\(t\)		 ['real']
  • time: 1
 time 121
1464 variable x
\(x\)		 ['real'] dimensionless 140
1575 variable \theta
\(\theta\)		 ['real'] dimensionless angle 34
5647 variable y
\(y\)		 ['real']
  • length: 1
 position 14
1572 variable x_0
\(x_0\)		 ['real']
  • length: 1
 initial position 11
3652 variable x_f
\(x_f\)		 real
  • length: 1
 final position on x axis 3
3141 constant \pi
\(\pi\)		 ['real'] dimensionless pi 3.1415   dimensionless
 72
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
MESSAGE: