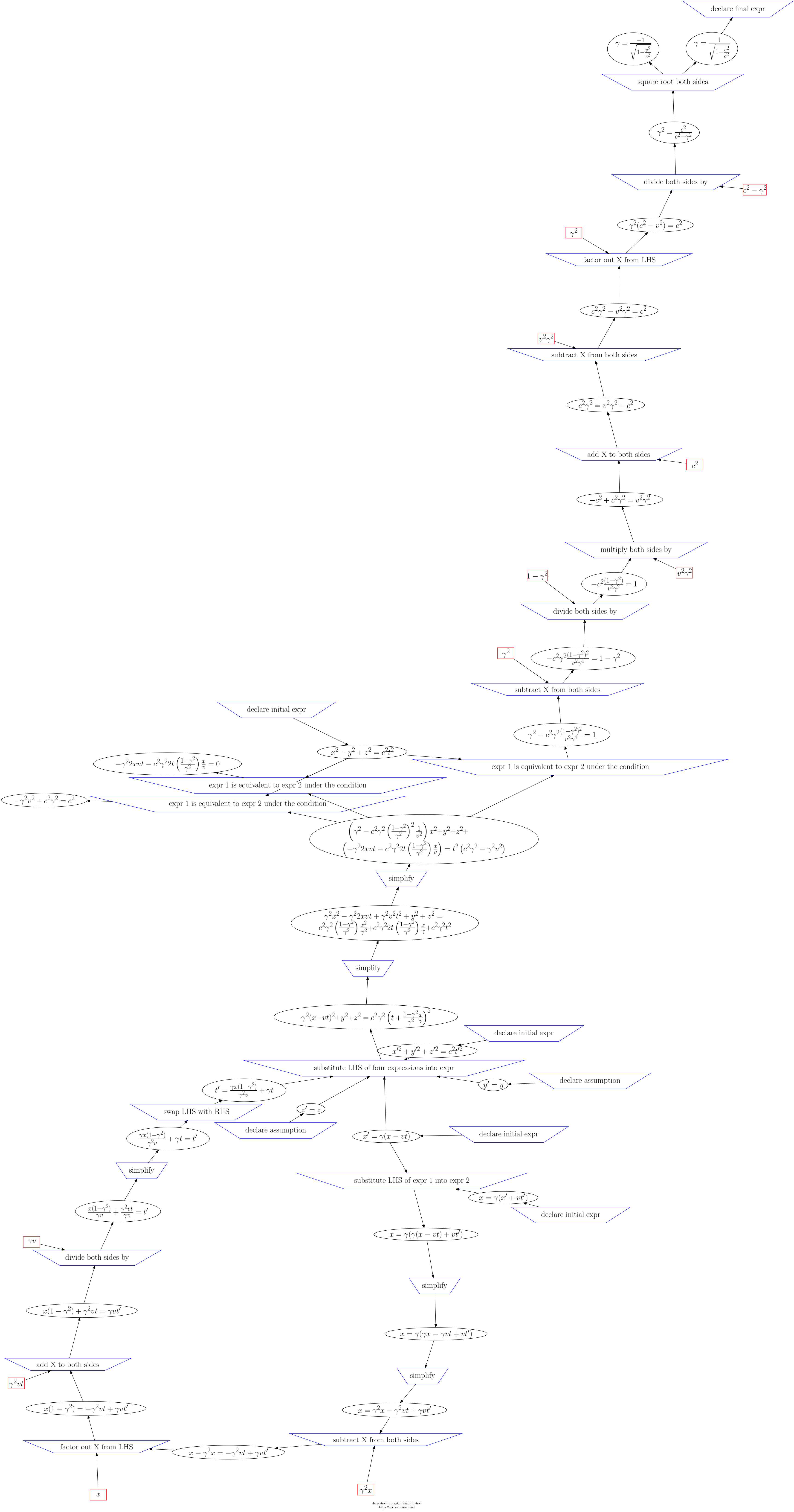
Physics Derivation Graph navigation Sign in

review derivation: Lorentz transformation

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
source: \cite{1999_Tipler_Llewellyn}, page 21; see also https://en.wikipedia.org/wiki/Lorentz_transformation and https://en.wikipedia.org/wiki/Derivations_of_the_Lorentz_transformations

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
20 expr 1 is equivalent to expr 2 under the condition
  1. 4287102261; locally 6319661:
    \(x^2 + y^2 + z^2 = c^2 t^2\)
    \(pdg_{4037}^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1467}^{2} pdg_{4567}^{2}\)
  2. 1586866563; locally 4202425:
    \(\left( \gamma^2 - c^2 \gamma^2 \left( \frac{1-\gamma^2}{\gamma^2} \right)^2 \frac{1}{v^2} \right) x^2 + y^2 + z^2 + \left( -\gamma^2 2 x v t - c^2 \gamma^2 2 t \left( \frac{1-\gamma^2}{\gamma^2} \right) \frac{x}{v} \right) = t^2 \left( c^2 \gamma^2 - \gamma^2 v^2 \right)\)
    \(- 2 pdg_{1357} pdg_{1467} pdg_{1790}^{2} pdg_{4037} + pdg_{4037}^{2} \left(pdg_{1790}^{2} - \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}}\right) + pdg_{5647}^{2} + pdg_{6728}^{2} - \frac{2 pdg_{1467} pdg_{4037} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357}} = pdg_{1467}^{2} \left(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2}\right)\)
  1. 1916173354; locally 3640931:
    \(-\gamma^2 v^2 + c^2 \gamma^2 = c^2\)
    \(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2} = pdg_{4567}^{2}\)
no check performed 4287102261:
1586866563:
1916173354:
4287102261:
1586866563:
1916173354:
based on the comparison of the t^2 terms
1 declare initial expr
  1. 4662369843; locally 5427510:
    \(x' = \gamma (x - v t)\)
    \(pdg_{5456} = pdg_{1790} \left(- pdg_{1357} pdg_{1467} + pdg_{1464}\right)\)
no validation is available for declarations 4662369843:
4662369843:
equation 1-13 on page 21 in \cite{1999_Tipler_Llewellyn}
15 declare assumption
  1. 8515803375; locally 7666907:
    \(z' = z\)
    \(pdg_{4306} = pdg_{6728}\)
no validation is available for declarations 8515803375:
8515803375:
11 swap LHS with RHS
  1. 8730201316; locally 7546640:
    \(\frac{\gamma x (1 - \gamma^2 )}{\gamma^2 v} + \gamma t = t'\)
    \(pdg_{1790}\)
  1. 5148266645; locally 1693888:
    \(t' = \frac{\gamma x (1 - \gamma^2 )}{\gamma^2 v} + \gamma t\)
    \(pdg_{1790}\)
Nothing to split 8730201316:
5148266645:
8730201316:
5148266645:
12 declare initial expr
  1. 4287102261; locally 6319661:
    \(x^2 + y^2 + z^2 = c^2 t^2\)
    \(pdg_{4037}^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1467}^{2} pdg_{4567}^{2}\)
no validation is available for declarations 4287102261:
4287102261:
25 add X to both sides
  1. 5763749235; locally 8195408:
    \(-c^2 + c^2 \gamma^2 = v^2 \gamma^2\)
    \(pdg_{1790}^{2} pdg_{4567}^{2} - pdg_{4567}^{2} = pdg_{1357}^{2} pdg_{1790}^{2}\)
  1. 6408214498:
    \(c^2\)
    \(pdg_{4567}^{2}\)
  1. 2999795755; locally 6913493:
    \(c^2 \gamma^2 = v^2 \gamma^2 + c^2\)
    \(pdg_{1790}^{2} pdg_{4567}^{2} = pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{4567}^{2}\)
valid 5763749235:
2999795755:
5763749235:
2999795755:
6 subtract X from both sides
  1. 7741202861; locally 6463955:
    \(x = \gamma^2 x - \gamma^2 v t + \gamma v t'\)
    \(pdg_{4037} = - pdg_{1357} pdg_{1467} pdg_{1790}^{2} + pdg_{1357} pdg_{1790} pdg_{4989} + pdg_{1790}^{2} pdg_{4037}\)
  1. 7337056406:
    \(\gamma^2 x\)
    \(pdg_{1790}^{2} pdg_{4037}\)
  1. 4139999399; locally 8494407:
    \(x - \gamma^2 x = - \gamma^2 v t + \gamma v t'\)
    \(- pdg_{1790}^{2} pdg_{4037} + pdg_{4037} = - pdg_{1357} pdg_{1467} pdg_{1790}^{2} + pdg_{1357} pdg_{1790} pdg_{4989}\)
valid 7741202861:
4139999399:
7741202861:
4139999399:
23 divide both sides by
  1. 2417941373; locally 7403799:
    \(- c^2 \gamma^2 \frac{(1-\gamma^2)^2}{v^2 \gamma^4} = 1 - \gamma^2\)
    \(- \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}} = 1 - pdg_{1790}^{2}\)
  1. 5787469164:
    \(1 - \gamma^2\)
    \(1 - pdg_{1790}^{2}\)
  1. 1639827492; locally 4052253:
    \(- c^2 \frac{(1-\gamma^2)}{v^2 \gamma^2} = 1\)
    \(- \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357}^{2} pdg_{1790}^{2}} = 1\)
valid 2417941373:
1639827492:
2417941373:
1639827492:
24 multiply both sides by
  1. 1639827492; locally 4052253:
    \(- c^2 \frac{(1-\gamma^2)}{v^2 \gamma^2} = 1\)
    \(- \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357}^{2} pdg_{1790}^{2}} = 1\)
  1. 5669500954:
    \(v^2 \gamma^2\)
    \(pdg_{1357}^{2} pdg_{1790}^{2}\)
  1. 5763749235; locally 8195408:
    \(-c^2 + c^2 \gamma^2 = v^2 \gamma^2\)
    \(pdg_{1790}^{2} pdg_{4567}^{2} - pdg_{4567}^{2} = pdg_{1357}^{2} pdg_{1790}^{2}\)
valid 1639827492:
5763749235:
1639827492:
5763749235:
10 simplify
  1. 1974334644; locally 5995189:
    \(\frac{x (1 - \gamma^2 )}{\gamma v} + \frac{\gamma^2 v t}{\gamma v} = t'\)
    \(pdg_{1467} pdg_{1790} + \frac{\operatorname{pdg}_{4037}{\left(1 - pdg_{1790}^{2} \right)}}{pdg_{1357} pdg_{1790}} = pdg_{4989}\)
  1. 8730201316; locally 7546640:
    \(\frac{\gamma x (1 - \gamma^2 )}{\gamma^2 v} + \gamma t = t'\)
    \(pdg_{1790}\)
Nothing to split 1974334644:
8730201316:
1974334644:
8730201316:
4 simplify
  1. 3426941928; locally 4471422:
    \(x = \gamma ( \gamma (x - v t) + v t' )\)
    \(pdg_{4037} = pdg_{1790} \left(pdg_{1357} pdg_{4989} + pdg_{1790} \left(- pdg_{1357} pdg_{1467} + pdg_{4037}\right)\right)\)
  1. 2096918413; locally 7169020:
    \(x = \gamma ( \gamma x - \gamma v t + v t' )\)
    \(pdg_{4037} = \operatorname{pdg}_{1790}{\left(- pdg_{1357} pdg_{1467} pdg_{1790} + pdg_{1357} pdg_{4989} + pdg_{1790} pdg_{4037} \right)}\)
LHS diff is 0 RHS diff is pdg1790*(pdg1357*pdg4989 - pdg1790*(pdg1357*pdg1467 - pdg4037)) - pdg1790(-pdg1357*pdg1467*pdg1790 + pdg1357*pdg4989 + pdg1790*pdg4037) 3426941928:
2096918413:
3426941928:
2096918413:
19 expr 1 is equivalent to expr 2 under the condition
  1. 4287102261; locally 6319661:
    \(x^2 + y^2 + z^2 = c^2 t^2\)
    \(pdg_{4037}^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1467}^{2} pdg_{4567}^{2}\)
  2. 1586866563; locally 4202425:
    \(\left( \gamma^2 - c^2 \gamma^2 \left( \frac{1-\gamma^2}{\gamma^2} \right)^2 \frac{1}{v^2} \right) x^2 + y^2 + z^2 + \left( -\gamma^2 2 x v t - c^2 \gamma^2 2 t \left( \frac{1-\gamma^2}{\gamma^2} \right) \frac{x}{v} \right) = t^2 \left( c^2 \gamma^2 - \gamma^2 v^2 \right)\)
    \(- 2 pdg_{1357} pdg_{1467} pdg_{1790}^{2} pdg_{4037} + pdg_{4037}^{2} \left(pdg_{1790}^{2} - \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}}\right) + pdg_{5647}^{2} + pdg_{6728}^{2} - \frac{2 pdg_{1467} pdg_{4037} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357}} = pdg_{1467}^{2} \left(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2}\right)\)
  1. 3182633789; locally 2562123:
    \(\gamma^2 - c^2 \gamma^2 \frac{(1-\gamma^2)^2}{v^2 \gamma^4} = 1\)
    \(pdg_{1790}^{2} - \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}} = 1\)
no check performed 4287102261:
1586866563:
3182633789:
4287102261:
1586866563:
3182633789:
based on the comparison of the x^2 terms
22 subtract X from both sides
  1. 3182633789; locally 2562123:
    \(\gamma^2 - c^2 \gamma^2 \frac{(1-\gamma^2)^2}{v^2 \gamma^4} = 1\)
    \(pdg_{1790}^{2} - \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}} = 1\)
  1. 5284610349:
    \(\gamma^2\)
    \(pdg_{1790}^{2}\)
  1. 2417941373; locally 7403799:
    \(- c^2 \gamma^2 \frac{(1-\gamma^2)^2}{v^2 \gamma^4} = 1 - \gamma^2\)
    \(- \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}} = 1 - pdg_{1790}^{2}\)
valid 3182633789:
2417941373:
3182633789:
2417941373:
solve for \gamma
29 square root both sides
  1. 7906112355; locally 7595841:
    \(\gamma^2 = \frac{c^2}{c^2 - \gamma^2}\)
    \(pdg_{1790}^{2} = \frac{pdg_{4567}^{2}}{- pdg_{1790}^{2} + pdg_{4567}^{2}}\)
  1. 1528310784; locally 3040283:
    \(\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)
    \(pdg_{1790} = \frac{1}{\sqrt{- \frac{pdg_{1357}^{2}}{pdg_{4567}^{2}} + 1}}\)
  2. 8360117126; locally 6010461:
    \(\gamma = \frac{-1}{\sqrt{1-\frac{v^2}{c^2}}}\)
    \(pdg_{1790} = - \frac{1}{\sqrt{- \frac{pdg_{1357}^{2}}{pdg_{4567}^{2}} + 1}}\)
no check performed 7906112355:
1528310784:
8360117126:
7906112355:
1528310784:
8360117126:
17 simplify
  1. 9805063945; locally 4326342:
    \(\gamma^2 (x - v t)^2 + y^2 + z^2 = c^2 \gamma^2 \left( t + \frac{ 1 - \gamma^2 }{ \gamma^2 } \frac{x}{v} \right)^2\)
    \(pdg_{1790}^{2} \left(- pdg_{1357} pdg_{1467} + pdg_{4037}\right)^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1790}^{2} pdg_{4567}^{2} \left(pdg_{1467} + \frac{pdg_{4037} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357} pdg_{1790}^{2}}\right)^{2}\)
  1. 1935543849; locally 6066191:
    \(\gamma^2 x^2 - \gamma^2 2 x v t + \gamma^2 v^2 t^2 + y^2 + z^2 = c^2 \gamma^2 \left(\frac{1-\gamma^2}{\gamma^2}\right)\frac{x^2}{\gamma^2} + c^2 \gamma^2 2 t \left(\frac{1-\gamma^2}{\gamma^2}\right)\frac{x}{\gamma} + c^2 \gamma^2 t^2\)
    \(pdg_{1357}^{2} pdg_{1467}^{2} pdg_{1790}^{2} - 2 pdg_{1357} pdg_{1467} pdg_{1790}^{2} pdg_{4037} + pdg_{1790}^{2} pdg_{4037}^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1467}^{2} pdg_{1790}^{2} pdg_{4567}^{2} + \frac{2 pdg_{1467} pdg_{4037} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1790}} + \frac{pdg_{4037}^{2} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1790}^{2}}\)
LHS diff is 0 RHS diff is pdg4567**2*(-pdg1357**2*pdg1467**2*pdg1790**4 + 2*pdg1357**2*pdg1467*pdg1790*pdg4037*(pdg1790**2 - 1) + pdg1357**2*pdg4037**2*(pdg1790**2 - 1) + (pdg1357*pdg1467*pdg1790**2 - pdg4037*(pdg1790**2 - 1))**2)/(pdg1357**2*pdg1790**2) 9805063945:
1935543849:
9805063945:
1935543849:
expanded the squared terms
30 declare final expr
  1. 1528310784; locally 3040283:
    \(\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)
    \(pdg_{1790} = \frac{1}{\sqrt{- \frac{pdg_{1357}^{2}}{pdg_{4567}^{2}} + 1}}\)
no validation is available for declarations 1528310784:
1528310784:
Lorentz factor definition
13 declare initial expr
  1. 1201689765; locally 5649086:
    \(x'^2 + y'^2 + z'^2 = c^2 t'^2\)
    \(pdg_{1888}^{2} + pdg_{4306}^{2} + pdg_{5456}^{2} = pdg_{4567}^{2} pdg_{4989}^{2}\)
no validation is available for declarations 1201689765:
1201689765:
5 simplify
  1. 2096918413; locally 7169020:
    \(x = \gamma ( \gamma x - \gamma v t + v t' )\)
    \(pdg_{4037} = \operatorname{pdg}_{1790}{\left(- pdg_{1357} pdg_{1467} pdg_{1790} + pdg_{1357} pdg_{4989} + pdg_{1790} pdg_{4037} \right)}\)
  1. 7741202861; locally 6463955:
    \(x = \gamma^2 x - \gamma^2 v t + \gamma v t'\)
    \(pdg_{4037} = - pdg_{1357} pdg_{1467} pdg_{1790}^{2} + pdg_{1357} pdg_{1790} pdg_{4989} + pdg_{1790}^{2} pdg_{4037}\)
LHS diff is 0 RHS diff is pdg1357*pdg1467*pdg1790**2 - pdg1357*pdg1790*pdg4989 - pdg1790**2*pdg4037 + pdg1790(-pdg1357*pdg1467*pdg1790 + pdg1357*pdg4989 + pdg1790*pdg4037) 2096918413:
7741202861:
2096918413:
7741202861:
14 declare assumption
  1. 7057864873; locally 6316097:
    \(y' = y\)
    \(pdg_{1888} = pdg_{5647}\)
no validation is available for declarations 7057864873:
7057864873:
3 substitute LHS of expr 1 into expr 2
  1. 4662369843; locally 5427510:
    \(x' = \gamma (x - v t)\)
    \(pdg_{5456} = pdg_{1790} \left(- pdg_{1357} pdg_{1467} + pdg_{1464}\right)\)
  2. 2983053062; locally 2283140:
    \(x = \gamma (x' + v t')\)
    \(pdg_{4037} = pdg_{1790} \left(pdg_{1357} pdg_{4989} + pdg_{5456}\right)\)
  1. 3426941928; locally 4471422:
    \(x = \gamma ( \gamma (x - v t) + v t' )\)
    \(pdg_{4037} = pdg_{1790} \left(pdg_{1357} pdg_{4989} + pdg_{1790} \left(- pdg_{1357} pdg_{1467} + pdg_{4037}\right)\right)\)
LHS diff is 0 RHS diff is pdg1790**2*(pdg1464 - pdg4037) 4662369843:
2983053062: dimensions are consistent
3426941928:
4662369843:
2983053062: N/A
3426941928:
solve output expr for t'
9 divide both sides by
  1. 9409776983; locally 6047713:
    \(x (1 - \gamma^2 ) + \gamma^2 v t = \gamma v t'\)
    \(pdg_{1790}\)
  1. 2226340358:
    \(\gamma v\)
    \(pdg_{1357} pdg_{1790}\)
  1. 1974334644; locally 5995189:
    \(\frac{x (1 - \gamma^2 )}{\gamma v} + \frac{\gamma^2 v t}{\gamma v} = t'\)
    \(pdg_{1467} pdg_{1790} + \frac{\operatorname{pdg}_{4037}{\left(1 - pdg_{1790}^{2} \right)}}{pdg_{1357} pdg_{1790}} = pdg_{4989}\)
Nothing to split 9409776983:
1974334644:
9409776983:
1974334644:
18 simplify
  1. 1935543849; locally 6066191:
    \(\gamma^2 x^2 - \gamma^2 2 x v t + \gamma^2 v^2 t^2 + y^2 + z^2 = c^2 \gamma^2 \left(\frac{1-\gamma^2}{\gamma^2}\right)\frac{x^2}{\gamma^2} + c^2 \gamma^2 2 t \left(\frac{1-\gamma^2}{\gamma^2}\right)\frac{x}{\gamma} + c^2 \gamma^2 t^2\)
    \(pdg_{1357}^{2} pdg_{1467}^{2} pdg_{1790}^{2} - 2 pdg_{1357} pdg_{1467} pdg_{1790}^{2} pdg_{4037} + pdg_{1790}^{2} pdg_{4037}^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1467}^{2} pdg_{1790}^{2} pdg_{4567}^{2} + \frac{2 pdg_{1467} pdg_{4037} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1790}} + \frac{pdg_{4037}^{2} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1790}^{2}}\)
  1. 1586866563; locally 4202425:
    \(\left( \gamma^2 - c^2 \gamma^2 \left( \frac{1-\gamma^2}{\gamma^2} \right)^2 \frac{1}{v^2} \right) x^2 + y^2 + z^2 + \left( -\gamma^2 2 x v t - c^2 \gamma^2 2 t \left( \frac{1-\gamma^2}{\gamma^2} \right) \frac{x}{v} \right) = t^2 \left( c^2 \gamma^2 - \gamma^2 v^2 \right)\)
    \(- 2 pdg_{1357} pdg_{1467} pdg_{1790}^{2} pdg_{4037} + pdg_{4037}^{2} \left(pdg_{1790}^{2} - \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}}\right) + pdg_{5647}^{2} + pdg_{6728}^{2} - \frac{2 pdg_{1467} pdg_{4037} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357}} = pdg_{1467}^{2} \left(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2}\right)\)
LHS diff is pdg1357**2*pdg1467**2*pdg1790**2 - 2*pdg1467*pdg1790**2*pdg4037*pdg4567**2/pdg1357 + 2*pdg1467*pdg4037*pdg4567**2/pdg1357 + pdg4037**2*pdg4567**2*(pdg1790**2 - 1)**2/(pdg1357**2*pdg1790**2) RHS diff is (pdg1357**2*pdg1467**2*pdg1790**4 - 2*pdg1467*pdg1790*pdg4037*pdg4567**2*(pdg1790**2 - 1) - pdg4037**2*pdg4567**2*(pdg1790**2 - 1))/pdg1790**2 1935543849:
1586866563:
1935543849:
1586866563:
grouped by terms for x^2, xt, and t^2
27 factor out X from LHS
  1. 2542420160; locally 5207615:
    \(c^2 \gamma^2 - v^2 \gamma^2 = c^2\)
    \(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2} = pdg_{4567}^{2}\)
  1. 7743841045:
    \(\gamma^2\)
    \(pdg_{1790}^{2}\)
  1. 7513513483; locally 8842089:
    \(\gamma^2 (c^2 - v^2) = c^2\)
    \(pdg_{1790}^{2} \left(- pdg_{1357}^{2} + pdg_{4567}^{2}\right) = pdg_{4567}^{2}\)
valid 2542420160:
7513513483:
2542420160:
7513513483:
21 expr 1 is equivalent to expr 2 under the condition
  1. 4287102261; locally 6319661:
    \(x^2 + y^2 + z^2 = c^2 t^2\)
    \(pdg_{4037}^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1467}^{2} pdg_{4567}^{2}\)
  2. 1586866563; locally 4202425:
    \(\left( \gamma^2 - c^2 \gamma^2 \left( \frac{1-\gamma^2}{\gamma^2} \right)^2 \frac{1}{v^2} \right) x^2 + y^2 + z^2 + \left( -\gamma^2 2 x v t - c^2 \gamma^2 2 t \left( \frac{1-\gamma^2}{\gamma^2} \right) \frac{x}{v} \right) = t^2 \left( c^2 \gamma^2 - \gamma^2 v^2 \right)\)
    \(- 2 pdg_{1357} pdg_{1467} pdg_{1790}^{2} pdg_{4037} + pdg_{4037}^{2} \left(pdg_{1790}^{2} - \frac{pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)^{2}}{pdg_{1357}^{2} pdg_{1790}^{2}}\right) + pdg_{5647}^{2} + pdg_{6728}^{2} - \frac{2 pdg_{1467} pdg_{4037} pdg_{4567}^{2} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357}} = pdg_{1467}^{2} \left(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2}\right)\)
  1. 2076171250; locally 6685577:
    \(-\gamma^2 2 x v t - c^2 \gamma^2 2 t \left( \frac{1-\gamma^2}{\gamma^2} \right) \frac{x}{v} = 0\)
    \(pdg_{1790}\)
Nothing to split 4287102261:
1586866563:
2076171250:
4287102261:
1586866563:
2076171250:
based on the comparison of the (x t) terms
16 substitute LHS of four expressions into expr
  1. 8515803375; locally 7666907:
    \(z' = z\)
    \(pdg_{4306} = pdg_{6728}\)
  2. 7057864873; locally 6316097:
    \(y' = y\)
    \(pdg_{1888} = pdg_{5647}\)
  3. 5148266645; locally 1693888:
    \(t' = \frac{\gamma x (1 - \gamma^2 )}{\gamma^2 v} + \gamma t\)
    \(pdg_{1790}\)
  4. 4662369843; locally 5427510:
    \(x' = \gamma (x - v t)\)
    \(pdg_{5456} = pdg_{1790} \left(- pdg_{1357} pdg_{1467} + pdg_{1464}\right)\)
  5. 1201689765; locally 5649086:
    \(x'^2 + y'^2 + z'^2 = c^2 t'^2\)
    \(pdg_{1888}^{2} + pdg_{4306}^{2} + pdg_{5456}^{2} = pdg_{4567}^{2} pdg_{4989}^{2}\)
  1. 9805063945; locally 4326342:
    \(\gamma^2 (x - v t)^2 + y^2 + z^2 = c^2 \gamma^2 \left( t + \frac{ 1 - \gamma^2 }{ \gamma^2 } \frac{x}{v} \right)^2\)
    \(pdg_{1790}^{2} \left(- pdg_{1357} pdg_{1467} + pdg_{4037}\right)^{2} + pdg_{5647}^{2} + pdg_{6728}^{2} = pdg_{1790}^{2} pdg_{4567}^{2} \left(pdg_{1467} + \frac{pdg_{4037} \left(1 - pdg_{1790}^{2}\right)}{pdg_{1357} pdg_{1790}^{2}}\right)^{2}\)
Nothing to split 8515803375:
7057864873:
5148266645:
4662369843:
1201689765:
9805063945:
8515803375:
7057864873:
5148266645:
4662369843:
1201689765:
9805063945:
8 add X to both sides
  1. 9031609275; locally 3992172:
    \(x (1 - \gamma^2 ) = - \gamma^2 v t + \gamma v t'\)
    \(pdg_{1790}\)
  1. 8014566709:
    \(\gamma^2 v t\)
    \(pdg_{1357} pdg_{1467} pdg_{1790}^{2}\)
  1. 9409776983; locally 6047713:
    \(x (1 - \gamma^2 ) + \gamma^2 v t = \gamma v t'\)
    \(pdg_{1790}\)
Nothing to split 9031609275:
9409776983:
9031609275:
9409776983:
26 subtract X from both sides
  1. 2999795755; locally 6913493:
    \(c^2 \gamma^2 = v^2 \gamma^2 + c^2\)
    \(pdg_{1790}^{2} pdg_{4567}^{2} = pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{4567}^{2}\)
  1. 3412946408:
    \(v^2 \gamma^2\)
    \(pdg_{1357}^{2} pdg_{1790}^{2}\)
  1. 2542420160; locally 5207615:
    \(c^2 \gamma^2 - v^2 \gamma^2 = c^2\)
    \(- pdg_{1357}^{2} pdg_{1790}^{2} + pdg_{1790}^{2} pdg_{4567}^{2} = pdg_{4567}^{2}\)
valid 2999795755:
2542420160:
2999795755:
2542420160:
28 divide both sides by
  1. 7513513483; locally 8842089:
    \(\gamma^2 (c^2 - v^2) = c^2\)
    \(pdg_{1790}^{2} \left(- pdg_{1357}^{2} + pdg_{4567}^{2}\right) = pdg_{4567}^{2}\)
  1. 8571466509:
    \(c^2 - \gamma^2\)
    \(- pdg_{1790}^{2} + pdg_{4567}^{2}\)
  1. 7906112355; locally 7595841:
    \(\gamma^2 = \frac{c^2}{c^2 - \gamma^2}\)
    \(pdg_{1790}^{2} = \frac{pdg_{4567}^{2}}{- pdg_{1790}^{2} + pdg_{4567}^{2}}\)
LHS diff is pdg1790**2*(pdg1357**2 - pdg1790**2)/(pdg1790**2 - pdg4567**2) RHS diff is 0 7513513483:
7906112355:
7513513483:
7906112355:
7 factor out X from LHS
  1. 4139999399; locally 8494407:
    \(x - \gamma^2 x = - \gamma^2 v t + \gamma v t'\)
    \(- pdg_{1790}^{2} pdg_{4037} + pdg_{4037} = - pdg_{1357} pdg_{1467} pdg_{1790}^{2} + pdg_{1357} pdg_{1790} pdg_{4989}\)
  1. 3495403335:
    \(x\)
    \(pdg_{1464}\)
  1. 9031609275; locally 3992172:
    \(x (1 - \gamma^2 ) = - \gamma^2 v t + \gamma v t'\)
    \(pdg_{1790}\)
Nothing to split 4139999399:
9031609275:
4139999399:
9031609275:
2 declare initial expr
  1. 2983053062; locally 2283140:
    \(x = \gamma (x' + v t')\)
    \(pdg_{4037} = pdg_{1790} \left(pdg_{1357} pdg_{4989} + pdg_{5456}\right)\)
no validation is available for declarations 2983053062: dimensions are consistent
 2983053062: N/A
 equation 1-14 on page 21 in \cite{1999_Tipler_Llewellyn}
Physics Derivation Graph: Steps for Lorentz transformation

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
1888 variable y'
\(y'\)		 ['real']
  • length: 1
 position in moving reference frame 2
5647 variable y
\(y\)		 ['real']
  • length: 1
 position 14
5456 variable x'
\(x'\)		 ['real']
  • length: 1
 position in moving reference frame 3
1357 variable v
\(v\)		 ['real']
  • length: 1
  • time: -1
 velocity 83
4306 variable z'
\(z'\)		 ['real']
  • length: 1
 position in moving reference frame 2
4989 variable t'
\(t'\)		 real
  • time: 1
 time in moving reference frame
  • str_note
7
6728 variable z
\(z\)		 ['real']
  • length: 1
 position 5
4567 constant c
\(c\)		 ['real']
  • length: 1
  • time: -1
 speed of light in vacuum 299792458   meters/second
 32
1464 variable x
\(x\)		 ['real'] dimensionless 140
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
1467 variable t
\(t\)		 ['real']
  • time: 1
 time 121
1790 variable \gamma
\(\gamma\)		 ['real'] dimensionless Lorentz factor 35
MESSAGE: