Physics Derivation Graph navigation Sign in

review derivation: optics: Law of refraction to Brewster's angle

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
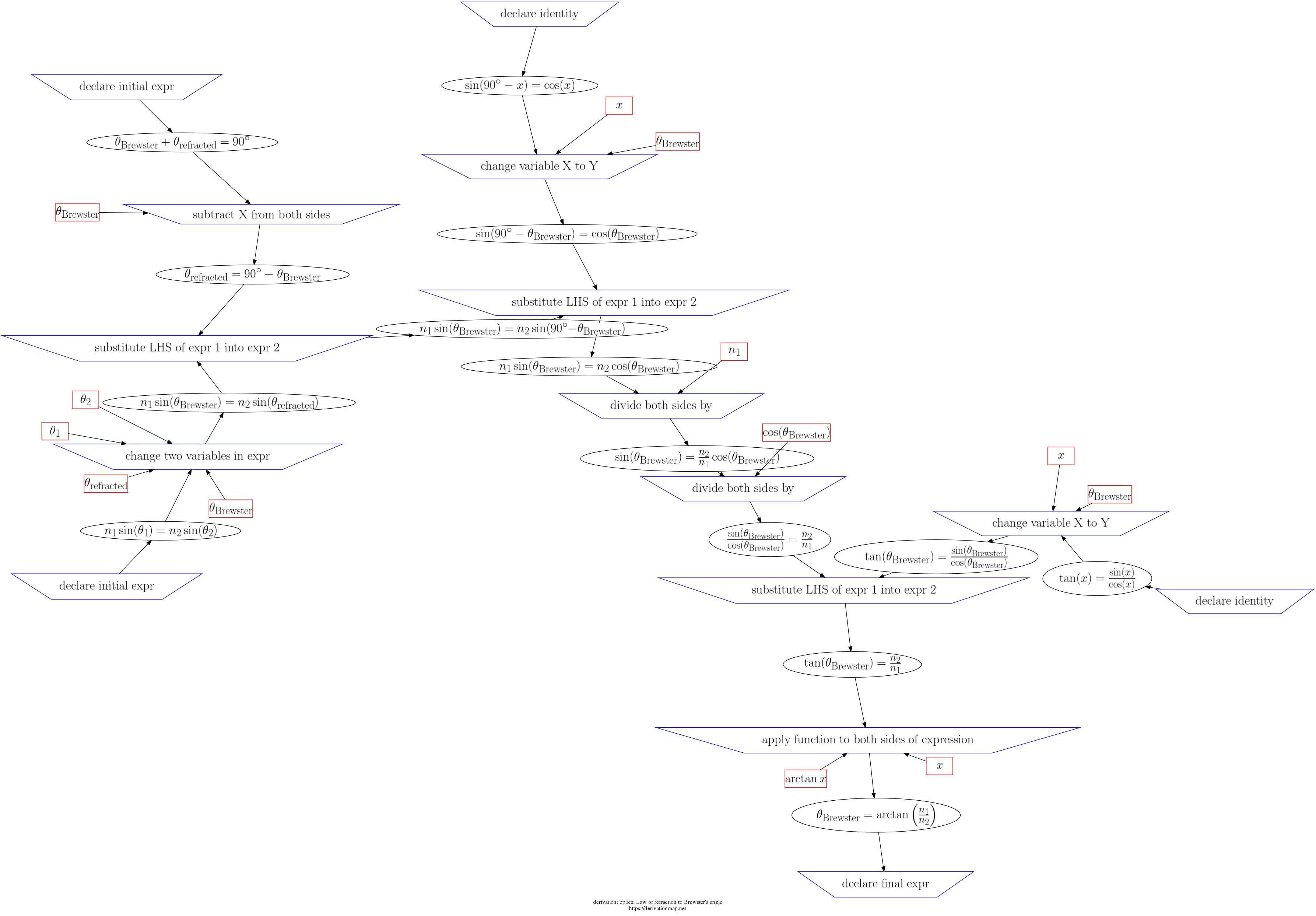
\cite{2001_HRW}; see figure 34-27 on page 824

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
6 declare identity
  1. 8588429722; locally 3940135:
    \(\sin( 90^{\circ} - x ) = \cos( x )\)
    \(- \sin{\left(pdg_{1464} - 90 \right)} = \cos{\left(pdg_{1464} \right)}\)
no validation is available for declarations 8588429722:
8588429722:
8 substitute LHS of expr 1 into expr 2
  1. 6831637424; locally 7426234:
    \(\sin( 90^{\circ} - \theta_{\rm Brewster} ) = \cos( \theta_{\rm Brewster} )\)
    \(pdg_{4928}\)
  2. 7696214507; locally 4962698:
    \(n_1 \sin( \theta_{\rm Brewster} ) = n_2 \sin( 90^{\circ} - \theta_{\rm Brewster} )\)
    \(pdg_{2941} \sin{\left(pdg_{4928} \right)} = - pdg_{1958} \sin{\left(pdg_{4928} - 90 \right)}\)
  1. 3061811650; locally 9701820:
    \(n_1 \sin( \theta_{\rm Brewster} ) = n_2 \cos( \theta_{\rm Brewster} )\)
    \(pdg_{2941} \sin{\left(pdg_{4928} \right)} = pdg_{1958} \cos{\left(pdg_{4928} \right)}\)
Nothing to split 6831637424:
7696214507:
3061811650:
6831637424:
7696214507:
3061811650:
15 declare final expr
  1. 8495187962; locally 8186016:
    \(\theta_{\rm Brewster} = \arctan{ \left( \frac{ n_1 }{ n_2 } \right) }\)
    \(pdg_{4928} = \operatorname{atan}{\left(\frac{pdg_{2941}}{pdg_{1958}} \right)}\)
no validation is available for declarations 8495187962:
8495187962:
3 declare initial expr
  1. 6450985774; locally 9932375:
    \(n_1 \sin( \theta_1 ) = n_2 \sin( \theta_2 )\)
    \(pdg_{2941} \sin{\left(pdg_{3509} \right)} = pdg_{1958} \sin{\left(pdg_{7545} \right)}\)
no validation is available for declarations 6450985774:
6450985774:
11 declare identity
  1. 4968680693; locally 2621708:
    \(\tan( x ) = \frac{ \sin( x )}{\cos( x )}\)
    \(\tan{\left(pdg_{1464} \right)} = \frac{\sin{\left(pdg_{1464} \right)}}{\cos{\left(pdg_{1464} \right)}}\)
no validation is available for declarations 4968680693:
4968680693:
9 divide both sides by
  1. 3061811650; locally 9701820:
    \(n_1 \sin( \theta_{\rm Brewster} ) = n_2 \cos( \theta_{\rm Brewster} )\)
    \(pdg_{2941} \sin{\left(pdg_{4928} \right)} = pdg_{1958} \cos{\left(pdg_{4928} \right)}\)
  1. 7857757625:
    \(n_1\)
    \(pdg_{2941}\)
  1. 9756089533; locally 9314305:
    \(\sin( \theta_{\rm Brewster} ) = \frac{n_2}{n_1} \cos( \theta_{\rm Brewster} )\)
    \(\sin{\left(pdg_{4928} \right)} = \frac{pdg_{1958} \cos{\left(pdg_{4928} \right)}}{pdg_{2941}}\)
valid 3061811650:
9756089533:
3061811650:
9756089533:
5 substitute LHS of expr 1 into expr 2
  1. 1310571337; locally 3893026:
    \(\theta_{\rm refracted} = 90^{\circ} - \theta_{\rm Brewster}\)
    \(pdg_{4928}\)
  2. 2575937347; locally 4176694:
    \(n_1 \sin( \theta_{\rm Brewster} ) = n_2 \sin( \theta_{\rm refracted} )\)
    \(pdg_{2941} \sin{\left(pdg_{4928} \right)} = pdg_{1958} \sin{\left(pdg_{2243} \right)}\)
  1. 7696214507; locally 4962698:
    \(n_1 \sin( \theta_{\rm Brewster} ) = n_2 \sin( 90^{\circ} - \theta_{\rm Brewster} )\)
    \(pdg_{2941} \sin{\left(pdg_{4928} \right)} = - pdg_{1958} \sin{\left(pdg_{4928} - 90 \right)}\)
Nothing to split 1310571337: no LHS/RHS split
2575937347:
7696214507:
1310571337: N/A
2575937347:
7696214507:
4 change two variables in expr
  1. 6450985774; locally 9932375:
    \(n_1 \sin( \theta_1 ) = n_2 \sin( \theta_2 )\)
    \(pdg_{2941} \sin{\left(pdg_{3509} \right)} = pdg_{1958} \sin{\left(pdg_{7545} \right)}\)
  1. 7154592211:
    \(\theta_2\)
    \(pdg_{7545}\)
  2. 6353701615:
    \(\theta_{\rm refracted}\)
    \(pdg_{2243}\)
  3. 2773628333:
    \(\theta_1\)
    \(pdg_{3509}\)
  4. 9029795851:
    \(\theta_{\rm Brewster}\)
    \(pdg_{4928}\)
  1. 2575937347; locally 4176694:
    \(n_1 \sin( \theta_{\rm Brewster} ) = n_2 \sin( \theta_{\rm refracted} )\)
    \(pdg_{2941} \sin{\left(pdg_{4928} \right)} = pdg_{1958} \sin{\left(pdg_{2243} \right)}\)
valid 6450985774:
2575937347:
6450985774:
2575937347:
12 change variable X to Y
  1. 4968680693; locally 2621708:
    \(\tan( x ) = \frac{ \sin( x )}{\cos( x )}\)
    \(\tan{\left(pdg_{1464} \right)} = \frac{\sin{\left(pdg_{1464} \right)}}{\cos{\left(pdg_{1464} \right)}}\)
  1. 7321695558:
    \(\theta_{\rm Brewster}\)
    \(pdg_{4928}\)
  2. 9906920183:
    \(x\)
    \(pdg_{1464}\)
  1. 4501377629; locally 1898054:
    \(\tan( \theta_{\rm Brewster} ) = \frac{ \sin( \theta_{\rm Brewster} )}{\cos( \theta_{\rm Brewster} )}\)
    \(\tan{\left(pdg_{4928} \right)} = \frac{\sin{\left(pdg_{4928} \right)}}{\cos{\left(pdg_{4928} \right)}}\)
LHS diff is tan(pdg1464) - tan(pdg4928) RHS diff is tan(pdg1464) - tan(pdg4928) 4968680693:
4501377629:
4968680693:
4501377629:
13 substitute LHS of expr 1 into expr 2
  1. 4501377629; locally 1898054:
    \(\tan( \theta_{\rm Brewster} ) = \frac{ \sin( \theta_{\rm Brewster} )}{\cos( \theta_{\rm Brewster} )}\)
    \(\tan{\left(pdg_{4928} \right)} = \frac{\sin{\left(pdg_{4928} \right)}}{\cos{\left(pdg_{4928} \right)}}\)
  2. 2768857871; locally 8585856:
    \(\frac{\sin( \theta_{\rm Brewster} )}{\cos( \theta_{\rm Brewster} )} = \frac{n_2}{n_1}\)
    \(\frac{\sin{\left(pdg_{4928} \right)}}{\cos{\left(pdg_{4928} \right)}} = \frac{pdg_{1958}}{pdg_{2941}}\)
  1. 3417126140; locally 5179630:
    \(\tan( \theta_{\rm Brewster} ) = \frac{ n_2 }{ n_1 }\)
    \(\tan{\left(pdg_{4928} \right)} = \frac{pdg_{1958}}{pdg_{2941}}\)
valid 4501377629:
2768857871:
3417126140:
4501377629:
2768857871:
3417126140:
1 declare initial expr
  1. 8945218208; locally 5563180:
    \(\theta_{\rm Brewster} + \theta_{\rm refracted} = 90^{\circ}\)
    \(pdg_{4928}\)
no validation is available for declarations 8945218208: no LHS/RHS split
 8945218208: N/A
14 apply function to both sides of expression
  1. 3417126140; locally 5179630:
    \(\tan( \theta_{\rm Brewster} ) = \frac{ n_2 }{ n_1 }\)
    \(\tan{\left(pdg_{4928} \right)} = \frac{pdg_{1958}}{pdg_{2941}}\)
  1. 5453995431:
    \(\arctan{ x }\)
    \(\operatorname{atan}{\left(pdg_{1464} \right)}\)
  2. 6023986360:
    \(x\)
    \(pdg_{1464}\)
  1. 8495187962; locally 8186016:
    \(\theta_{\rm Brewster} = \arctan{ \left( \frac{ n_1 }{ n_2 } \right) }\)
    \(pdg_{4928} = \operatorname{atan}{\left(\frac{pdg_{2941}}{pdg_{1958}} \right)}\)
no check performed 3417126140:
8495187962:
3417126140:
8495187962:
10 divide both sides by
  1. 9756089533; locally 9314305:
    \(\sin( \theta_{\rm Brewster} ) = \frac{n_2}{n_1} \cos( \theta_{\rm Brewster} )\)
    \(\sin{\left(pdg_{4928} \right)} = \frac{pdg_{1958} \cos{\left(pdg_{4928} \right)}}{pdg_{2941}}\)
  1. 5632428182:
    \(\cos( \theta_{\rm Brewster} )\)
    \(\cos{\left(pdg_{4928} \right)}\)
  1. 2768857871; locally 8585856:
    \(\frac{\sin( \theta_{\rm Brewster} )}{\cos( \theta_{\rm Brewster} )} = \frac{n_2}{n_1}\)
    \(\frac{\sin{\left(pdg_{4928} \right)}}{\cos{\left(pdg_{4928} \right)}} = \frac{pdg_{1958}}{pdg_{2941}}\)
valid 9756089533:
2768857871:
9756089533:
2768857871:
7 change variable X to Y
  1. 8588429722; locally 3940135:
    \(\sin( 90^{\circ} - x ) = \cos( x )\)
    \(- \sin{\left(pdg_{1464} - 90 \right)} = \cos{\left(pdg_{1464} \right)}\)
  1. 7375348852:
    \(\theta_{\rm Brewster}\)
    \(pdg_{4928}\)
  2. 1512581563:
    \(x\)
    \(pdg_{1464}\)
  1. 6831637424; locally 7426234:
    \(\sin( 90^{\circ} - \theta_{\rm Brewster} ) = \cos( \theta_{\rm Brewster} )\)
    \(pdg_{4928}\)
Nothing to split 8588429722:
6831637424:
8588429722:
6831637424:
2 subtract X from both sides
  1. 8945218208; locally 5563180:
    \(\theta_{\rm Brewster} + \theta_{\rm refracted} = 90^{\circ}\)
    \(pdg_{4928}\)
  1. 9025853427:
    \(\theta_{\rm Brewster}\)
    \(pdg_{4928}\)
  1. 1310571337; locally 3893026:
    \(\theta_{\rm refracted} = 90^{\circ} - \theta_{\rm Brewster}\)
    \(pdg_{4928}\)
Nothing to split 8945218208: no LHS/RHS split
1310571337: no LHS/RHS split
 8945218208: N/A
1310571337: N/A
Physics Derivation Graph: Steps for optics: Law of refraction to Brewster's angle

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
2243 variable \theta_{\rm refracted}
\(\theta_{\rm refracted}\)		 real dimensionless refracted angle
  • str_note
2
1958 variable n_2
\(n_2\)		 real dimensionless index of refraction for material 2 8
3509 variable \theta_1
\(\theta_1\)		 real dimensionless angle 2
4928 variable \theta_{\rm Brewster}
\(\theta_{\rm Brewster}\)		 ['real'] dimensionless Brewster's angle 16
2941 variable n_1
\(n_1\)		 ['real'] dimensionless index of refraction for material 1 9
7545 variable \theta_2
\(\theta_2\)		 real dimensionless angle 2
1464 variable x
\(x\)		 ['real'] dimensionless 140
MESSAGE: