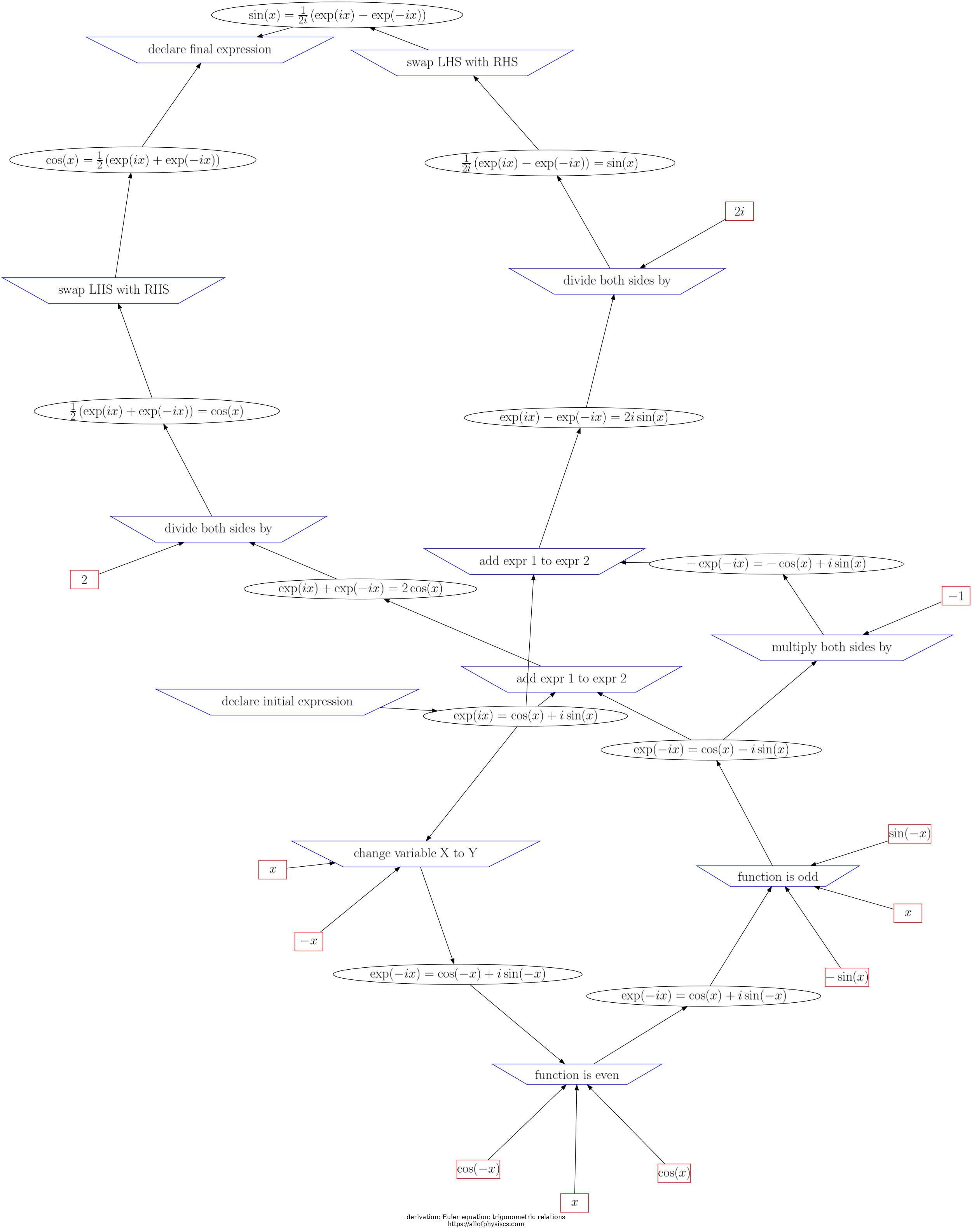
Welcome to the Physics Derivation Graph

Return to navigation page or list derivations

Review Euler equation: trigonometric relations

abstract:
reference:

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			4938429483 $\exp(i x)=\cos(x)+i \sin(x)$	no validation is available for declarations
2	111886: change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.	4938429483 $\exp(i x)=\cos(x)+i \sin(x)$	0003949052 $-x$ 0002393922 $x$	2394853829 $\exp(-i x)=\cos(-x)+i \sin(-x)$	LHS diff is 2sinh(pdg0001464pdg0004621) RHS diff is 2pdg0004621sin(pdg0001464)
3	111329: function is even number of inputs: 1; feeds: 3; outputs: 1 $#1$ is even with respect to $#2$, so replace $#1$ with $#3$ in Eq.~\\ref{eq:#4}; yields Eq.~\\ref{eq:#5}.	2394853829 $\exp(-i x)=\cos(-x)+i \sin(-x)$	0003413423 $\cos(-x)$ 0001030901 $\cos(x)$ 0004849392 $x$	4938429482 $\exp(-i x)=\cos(x)+i \sin(-x)$	recognized infrule but not yet supported
4	111522: function is odd number of inputs: 1; feeds: 3; outputs: 1 $#1$ is odd with respect to $#2$, so replace $#1$ with $#3$ in Eq.~\\ref{eq:#4}; yields Eq.~\\ref{eq:#5}.	4938429482 $\exp(-i x)=\cos(x)+i \sin(-x)$	0003919391 $x$ 0002919191 $\sin(-x)$ 0003981813 $-\sin(x)$	4938429484 $\exp(-i x)=\cos(x)-i \sin(x)$	recognized infrule but not yet supported
5	111980: add expr 1 to expr 2 number of inputs: 2; feeds: 0; outputs: 1 Add Eq.~\\ref{eq:#1} to Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#2}.	4938429483 $\exp(i x)=\cos(x)+i \sin(x)$ 4938429484 $\exp(-i x)=\cos(x)-i \sin(x)$		4742644828 $\exp(i x)+\exp(-i x)=2 \cos(x)$	valid
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	4742644828 $\exp(i x)+\exp(-i x)=2 \cos(x)$	0004829194 $2$	3829492824 $\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)=\cos(x)$	valid
7	111268: swap LHS with RHS number of inputs: 1; feeds: 0; outputs: 1 Swap LHS of Eq.~\\ref{eq:#1} with RHS; yields Eq.~\\ref{eq:#2}.	3829492824 $\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)=\cos(x)$		4585932229 $\cos(x)=\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)$	valid
8	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	2103023049 $\sin(x)=\frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)$ 4585932229 $\cos(x)=\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)$			no validation is available for declarations
9	111182: multiply both sides by number of inputs: 1; feeds: 1; outputs: 1 Multiply both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	4938429484 $\exp(-i x)=\cos(x)-i \sin(x)$	0003747849 $-1$	2123139121 $-\exp(-i x)=-\cos(x)+i \sin(x)$	valid
10	111980: add expr 1 to expr 2 number of inputs: 2; feeds: 0; outputs: 1 Add Eq.~\\ref{eq:#1} to Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#2}.	2123139121 $-\exp(-i x)=-\cos(x)+i \sin(x)$ 4938429483 $\exp(i x)=\cos(x)+i \sin(x)$		3942849294 $\exp(i x)-\exp(-i x)=2 i \sin(x)$	valid
11	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	3942849294 $\exp(i x)-\exp(-i x)=2 i \sin(x)$	0001921933 $2 i$	4843995999 $\frac{1}{2 i}\left(\exp(i x)-\exp(-i x) \right)=\sin(x)$	valid
12	111268: swap LHS with RHS number of inputs: 1; feeds: 0; outputs: 1 Swap LHS of Eq.~\\ref{eq:#1} with RHS; yields Eq.~\\ref{eq:#2}.	4843995999 $\frac{1}{2 i}\left(\exp(i x)-\exp(-i x) \right)=\sin(x)$		2103023049 $\sin(x)=\frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)$	valid

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.005 seconds for pdg_app/to_review_derivation: node_properties, derivation 7397408
0.003 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation8655509
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4291670
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4291670
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4291670
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4291670
0.005 seconds for compute/get_dict_of_steps_in_derivation: get_step_has_sequence_index8655509
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3184027
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3184027
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3184027
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3184027
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8024981
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8024981
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8024981
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8024981
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5689758
0.014 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5689758
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5689758
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5689758
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9221382
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9221382
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9221382
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9221382
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3188308
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3188308
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3188308
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3188308
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4482220
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4482220
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4482220
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4482220
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4815762
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4815762
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4815762
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4815762
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7205851
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7205851
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7205851
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7205851
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4818918
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4818918
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4818918
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4818918
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8206167
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8206167
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8206167
0.011 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8206167
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7265658
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7265658
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7265658
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7265658
0.003 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation7397408
0.007 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id7397408000003
0.018 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule7397408
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7017623
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7017623
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7017623
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7017623
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3279158
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3279158
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3279158
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3279158
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7427868
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7427868
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7427868
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7427868
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9358215
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9358215
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9358215
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9358215
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6150454
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6150454
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6150454
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6150454
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4874866
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4874866
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4874866
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4874866
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5911003
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5911003
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5911003
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5911003
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4215921
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4215921
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4215921
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4215921
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6077898
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6077898
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6077898
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6077898
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2803019
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2803019
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2803019
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2803019
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5380115
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5380115
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5380115
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5380115
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6095210
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6095210
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6095210
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6095210
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2163574
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2163574
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2163574
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2163574
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1915879
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1915879
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1915879
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1915879
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6369037
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6369037
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6369037
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6369037
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6488938
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6488938
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6488938
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6488938
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6779714
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6779714
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6779714
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6779714
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1986359
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1986359
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1986359
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1986359
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5489157
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5489157
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5489157
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5489157
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9819328
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9819328
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9819328
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9819328
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7740139
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7740139
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7740139
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7740139
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2425106
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2425106
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2425106
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2425106
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9409706
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9409706
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9409706
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9409706
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8811508
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8811508
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8811508
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8811508

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			4938429483 \(\exp(i x)=\cos(x)+i \sin(x)\)	no validation is available for declarations
2	111886: change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.	4938429483 \(\exp(i x)=\cos(x)+i \sin(x)\)	0003949052 \(-x\) 0002393922 \(x\)	2394853829 \(\exp(-i x)=\cos(-x)+i \sin(-x)\)	LHS diff is 2sinh(pdg0001464pdg0004621) RHS diff is 2pdg0004621sin(pdg0001464)
3	111329: function is even number of inputs: 1; feeds: 3; outputs: 1 $#1$ is even with respect to $#2$, so replace $#1$ with $#3$ in Eq.~\\ref{eq:#4}; yields Eq.~\\ref{eq:#5}.	2394853829 \(\exp(-i x)=\cos(-x)+i \sin(-x)\)	0003413423 \(\cos(-x)\) 0001030901 \(\cos(x)\) 0004849392 \(x\)	4938429482 \(\exp(-i x)=\cos(x)+i \sin(-x)\)	recognized infrule but not yet supported
4	111522: function is odd number of inputs: 1; feeds: 3; outputs: 1 $#1$ is odd with respect to $#2$, so replace $#1$ with $#3$ in Eq.~\\ref{eq:#4}; yields Eq.~\\ref{eq:#5}.	4938429482 \(\exp(-i x)=\cos(x)+i \sin(-x)\)	0003919391 \(x\) 0002919191 \(\sin(-x)\) 0003981813 \(-\sin(x)\)	4938429484 \(\exp(-i x)=\cos(x)-i \sin(x)\)	recognized infrule but not yet supported
5	111980: add expr 1 to expr 2 number of inputs: 2; feeds: 0; outputs: 1 Add Eq.~\\ref{eq:#1} to Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#2}.	4938429483 \(\exp(i x)=\cos(x)+i \sin(x)\) 4938429484 \(\exp(-i x)=\cos(x)-i \sin(x)\)		4742644828 \(\exp(i x)+\exp(-i x)=2 \cos(x)\)	valid
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	4742644828 \(\exp(i x)+\exp(-i x)=2 \cos(x)\)	0004829194 \(2\)	3829492824 \(\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)=\cos(x)\)	valid
7	111268: swap LHS with RHS number of inputs: 1; feeds: 0; outputs: 1 Swap LHS of Eq.~\\ref{eq:#1} with RHS; yields Eq.~\\ref{eq:#2}.	3829492824 \(\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)=\cos(x)\)		4585932229 \(\cos(x)=\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)\)	valid
8	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	2103023049 \(\sin(x)=\frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)\) 4585932229 \(\cos(x)=\frac{1}{2}\left(\exp(i x)+\exp(-i x) \right)\)			no validation is available for declarations
9	111182: multiply both sides by number of inputs: 1; feeds: 1; outputs: 1 Multiply both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	4938429484 \(\exp(-i x)=\cos(x)-i \sin(x)\)	0003747849 \(-1\)	2123139121 \(-\exp(-i x)=-\cos(x)+i \sin(x)\)	valid
10	111980: add expr 1 to expr 2 number of inputs: 2; feeds: 0; outputs: 1 Add Eq.~\\ref{eq:#1} to Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#2}.	2123139121 \(-\exp(-i x)=-\cos(x)+i \sin(x)\) 4938429483 \(\exp(i x)=\cos(x)+i \sin(x)\)		3942849294 \(\exp(i x)-\exp(-i x)=2 i \sin(x)\)	valid
11	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	3942849294 \(\exp(i x)-\exp(-i x)=2 i \sin(x)\)	0001921933 \(2 i\)	4843995999 \(\frac{1}{2 i}\left(\exp(i x)-\exp(-i x) \right)=\sin(x)\)	valid
12	111268: swap LHS with RHS number of inputs: 1; feeds: 0; outputs: 1 Swap LHS of Eq.~\\ref{eq:#1} with RHS; yields Eq.~\\ref{eq:#2}.	4843995999 \(\frac{1}{2 i}\left(\exp(i x)-\exp(-i x) \right)=\sin(x)\)		2103023049 \(\sin(x)=\frac{1}{2i}\left(\exp(i x)-\exp(-i x) \right)\)	valid