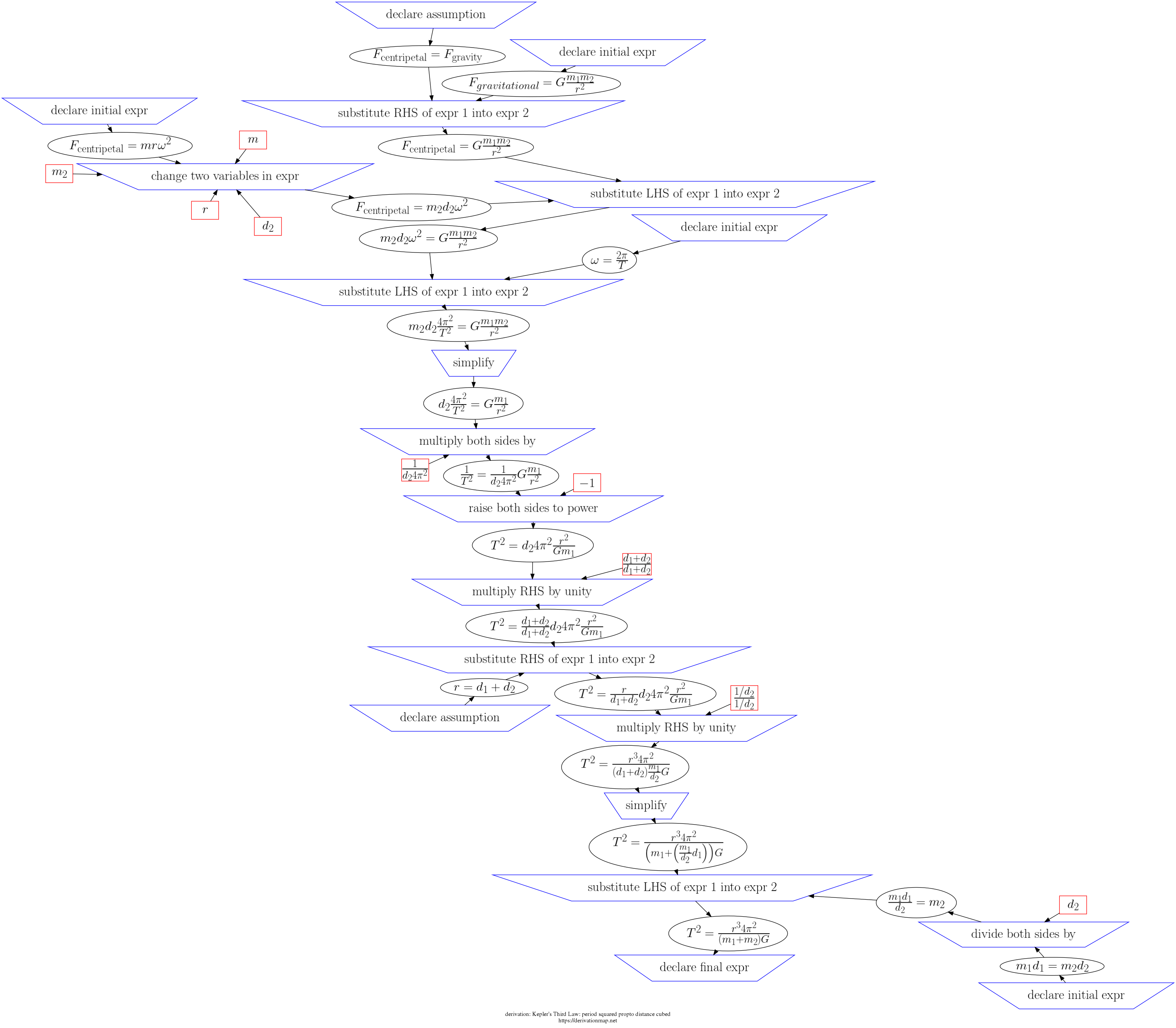
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion#Third_law
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 8 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
3132131132:
3896798826: 9070394000: |
3132131132:
3896798826: 9070394000: |
|
| 19 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
2217103163:
4188580242: 5658865948: |
2217103163:
4188580242: 5658865948: |
|
| 7 | declare initial expr |
|
|
|
no validation is available for declarations |
3132131132:
|
3132131132:
|
|
| 12 | multiply RHS by unity |
|
|
|
valid |
9170048197:
1811867899: |
9170048197:
1811867899: |
|
| 3 | change two variables in expr |
|
|
|
valid |
4393258808:
dimensions are consistent 3649797559: |
4393258808:
N/A 3649797559: |
|
| 11 | raise both sides to power |
|
|
|
no check is performed |
9152823411:
9170048197: |
9152823411:
9170048197: |
|
| 6 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
3649797559:
6829281943: 3896798826: |
3649797559:
6829281943: 3896798826: |
|
| 17 | declare initial expr |
|
|
|
no validation is available for declarations |
5128670694:
|
5128670694:
|
|
| 16 | simplify |
|
|
|
valid |
3781109867:
4188580242: |
3781109867:
4188580242: |
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
1292735067:
|
1292735067:
|
|
| 10 | multiply both sides by |
|
|
|
valid |
9838128064:
9152823411: |
9838128064:
9152823411: |
|
| 20 | declare final expr |
|
|
|
no validation is available for declarations |
5658865948:
|
5658865948:
|
period squared propto distance cubed |
| 15 | multiply RHS by unity |
|
|
|
valid |
2906548078:
3781109867: |
2906548078:
3781109867: |
|
| 13 | declare assumption |
|
|
|
no validation is available for declarations |
5586102077:
|
5586102077:
|
|
| 5 | substitute RHS of expr 1 into expr 2 |
|
|
|
LHS diff is -pdg1687 + pdg2867 RHS diff is 0 |
3176662571:
1292735067: 6829281943: |
3176662571:
1292735067: 6829281943: |
|
| 18 | divide both sides by |
|
|
|
valid |
5128670694:
2217103163: |
5128670694:
2217103163: |
|
| 4 | declare assumption |
|
|
|
no validation is available for declarations |
3176662571:
|
3176662571:
|
|
| 9 | simplify |
|
|
|
LHS diff is 4*pdg2798*pdg3141**2*(pdg4851 - 1)/pdg9491**2 RHS diff is pdg5022*pdg6277*(pdg4851 - 1)/pdg2530**2 |
9070394000:
9838128064: |
9070394000:
9838128064: |
|
| 14 | substitute RHS of expr 1 into expr 2 |
|
|
|
LHS diff is 0 RHS diff is 4*pdg2530**2*pdg2798*pdg3141**2*(-pdg2530 + pdg2798 + pdg7652)/(pdg5022*pdg6277*(pdg2798 + pdg7652)) |
5586102077:
1811867899: 2906548078: |
5586102077:
1811867899: 2906548078: |
|
| 2 | declare initial expr |
|
|
|
no validation is available for declarations |
4393258808:
dimensions are consistent |
4393258808:
N/A |