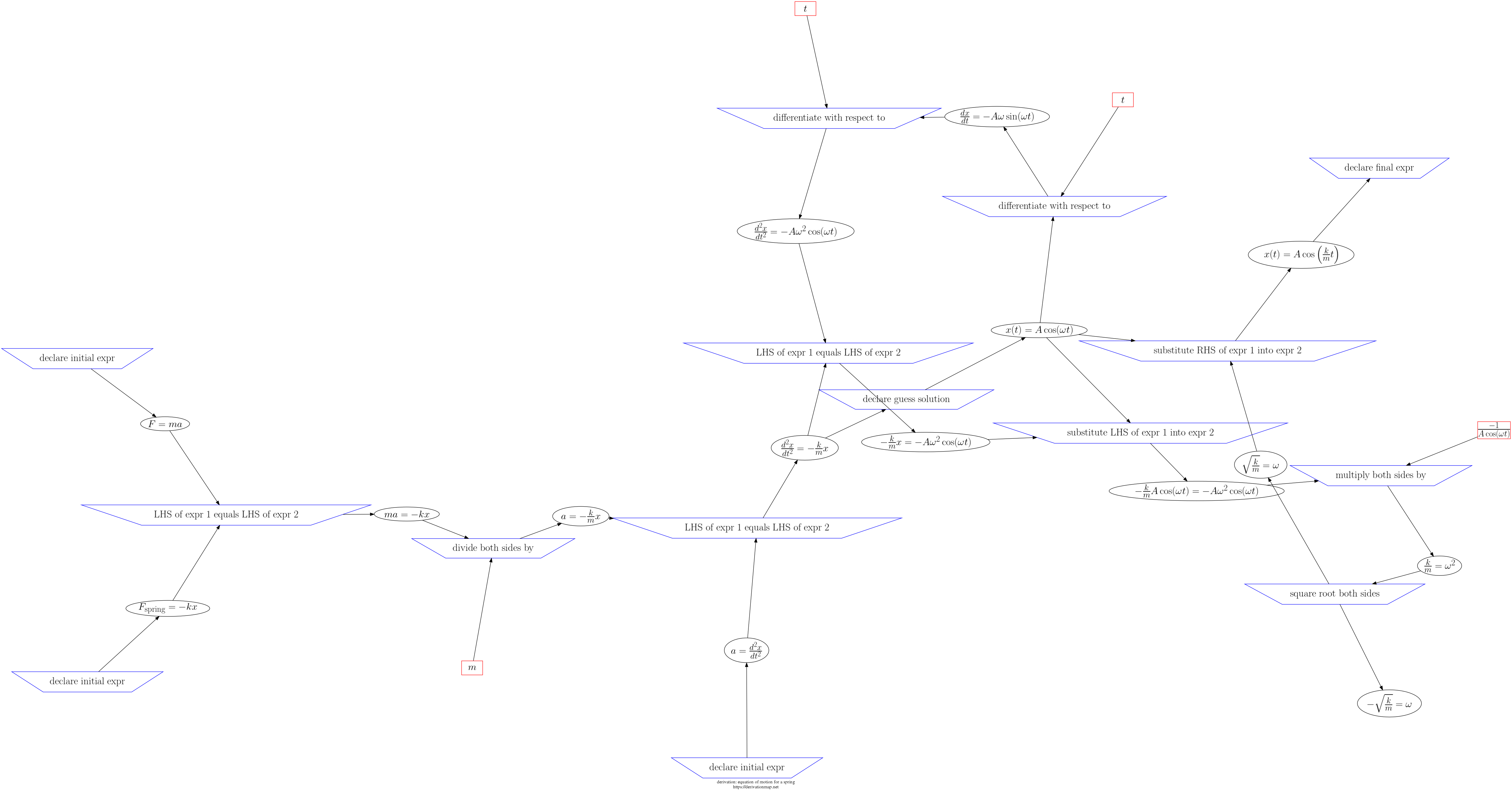
Physics Derivation Graph navigation Sign in

review derivation: equation of motion for a spring

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
3 declare initial expr
  1. 6831694380; locally 9761157:
    \(a = \frac{d^2 x}{dt^2}\)
    \(a = \frac{d^{2} x}{dt^{2}}\)
no validation is available for declarations 6831694380:
6831694380:
7 declare guess solution
  1. 8991236357; locally 4154219:
    \(\frac{d^2 x}{dt^2} = -\frac{k}{m} x\)
    \(\frac{d^{2} pdg_{4037}}{dt^{2}} = - \frac{pdg_{1356} pdg_{4037}}{pdg_{5156}}\)
  1. 5415824175; locally 2877569:
    \(x(t) = A \cos(\omega t)\)
    \(x{\left(pdg_{1467} \right)} = pdg_{9885} \cos{\left(pdg_{1467} pdg_{2321} \right)}\)
no validation is available for declarations 8991236357:
5415824175:
8991236357:
5415824175:
what, when differentiated twice, yields a negative of itself? cosine
10 LHS of expr 1 equals LHS of expr 2
  1. 5945893986; locally 4836115:
    \(\frac{d^2 x}{dt^2} = -A \omega^2 \cos(\omega t)\)
    \(\frac{d^{2} x}{dt^{2}} = - pdg_{2321}^{2} pdg_{9885} \cos{\left(pdg_{1467} pdg_{2321} \right)}\)
  2. 8991236357; locally 4154219:
    \(\frac{d^2 x}{dt^2} = -\frac{k}{m} x\)
    \(\frac{d^{2} pdg_{4037}}{dt^{2}} = - \frac{pdg_{1356} pdg_{4037}}{pdg_{5156}}\)
  1. 1772973171; locally 7792692:
    \(-\frac{k}{m} x = -A \omega^2 \cos(\omega t)\)
    \(- \frac{k x}{pdg_{5156}} = - A pdg_{2321}^{2} \cos{\left(pdg_{2321} pdg_{9491} \right)}\)
input diff is d**2*(-pdg4037 + x)/dt**2 diff is -k*x/pdg5156 + pdg2321**2*pdg9885*cos(pdg1467*pdg2321) diff is -A*pdg2321**2*cos(pdg2321*pdg9491) + pdg1356*pdg4037/pdg5156 5945893986:
8991236357:
1772973171:
5945893986:
8991236357:
1772973171:
11 substitute LHS of expr 1 into expr 2
  1. 5415824175; locally 2877569:
    \(x(t) = A \cos(\omega t)\)
    \(x{\left(pdg_{1467} \right)} = pdg_{9885} \cos{\left(pdg_{1467} pdg_{2321} \right)}\)
  2. 1772973171; locally 7792692:
    \(-\frac{k}{m} x = -A \omega^2 \cos(\omega t)\)
    \(- \frac{k x}{pdg_{5156}} = - A pdg_{2321}^{2} \cos{\left(pdg_{2321} pdg_{9491} \right)}\)
  1. 2148049269; locally 7745098:
    \(-\frac{k}{m} A \cos(\omega t) = -A \omega^2 \cos(\omega t)\)
    \(- \frac{A k \cos{\left(pdg_{2321} pdg_{9491} \right)}}{pdg_{5156}} = - A pdg_{2321}^{2} \cos{\left(pdg_{2321} pdg_{9491} \right)}\)
LHS diff is k*(A*cos(pdg2321*pdg9491) - x)/pdg5156 RHS diff is 0 5415824175:
1772973171:
2148049269:
5415824175:
1772973171:
2148049269:
13 square root both sides
  1. 1931103031; locally 8360924:
    \(\frac{k}{m} = \omega^2\)
    \(\frac{pdg_{1356}}{pdg_{5156}} = pdg_{2321}^{2}\)
  1. 1784114349; locally 7243628:
    \(\sqrt{\frac{k}{m}} = \omega\)
    \(\sqrt{\frac{pdg_{1356}}{pdg_{5156}}} = pdg_{2321}\)
  2. 1888494137; locally 2051755:
    \(-\sqrt{\frac{k}{m}} = \omega\)
    \(- \sqrt{\frac{pdg_{1356}}{pdg_{5156}}} = pdg_{2321}\)
no check performed 1931103031:
1784114349:
1888494137:
1931103031:
1784114349:
1888494137:
1 declare initial expr
  1. 5345738321; locally 3065061:
    \(F = m a\)
    \(pdg_{4202} = pdg_{5156} pdg_{9140}\)
no validation is available for declarations 5345738321:
5345738321:
2 declare initial expr
  1. 4428528271; locally 2664105:
    \(F_{\rm{spring}} = -k x\)
    \(pdg_{4183} = - pdg_{1356} pdg_{4037}\)
no validation is available for declarations 4428528271:
4428528271:
6 LHS of expr 1 equals LHS of expr 2
  1. 8655294002; locally 5403312:
    \(a = -\frac{k}{m}x\)
    \(pdg_{9140} = - \frac{pdg_{1356} pdg_{4037}}{pdg_{5156}}\)
  2. 6831694380; locally 9761157:
    \(a = \frac{d^2 x}{dt^2}\)
    \(a = \frac{d^{2} x}{dt^{2}}\)
  1. 8991236357; locally 4154219:
    \(\frac{d^2 x}{dt^2} = -\frac{k}{m} x\)
    \(\frac{d^{2} pdg_{4037}}{dt^{2}} = - \frac{pdg_{1356} pdg_{4037}}{pdg_{5156}}\)
input diff is -a + pdg9140 diff is d**2*pdg4037/dt**2 + pdg1356*pdg4037/pdg5156 diff is -d**2*x/dt**2 - pdg1356*pdg4037/pdg5156 8655294002:
6831694380:
8991236357:
8655294002:
6831694380:
8991236357:
4 LHS of expr 1 equals LHS of expr 2
  1. 5345738321; locally 3065061:
    \(F = m a\)
    \(pdg_{4202} = pdg_{5156} pdg_{9140}\)
  2. 4428528271; locally 2664105:
    \(F_{\rm{spring}} = -k x\)
    \(pdg_{4183} = - pdg_{1356} pdg_{4037}\)
  1. 2334518266; locally 7273319:
    \(m a = -k x\)
    \(pdg_{5156} pdg_{9140} = - pdg_{1356} pdg_{4037}\)
input diff is -pdg4183 + pdg4202 diff is 0 diff is 0 5345738321:
4428528271:
2334518266:
5345738321:
4428528271:
2334518266:
12 multiply both sides by
  1. 2148049269; locally 7745098:
    \(-\frac{k}{m} A \cos(\omega t) = -A \omega^2 \cos(\omega t)\)
    \(- \frac{A k \cos{\left(pdg_{2321} pdg_{9491} \right)}}{pdg_{5156}} = - A pdg_{2321}^{2} \cos{\left(pdg_{2321} pdg_{9491} \right)}\)
  1. 7473576008:
    \(\frac{-1}{A \cos(\omega t)}\)
    \(pdg_{1467}\)
  1. 1931103031; locally 8360924:
    \(\frac{k}{m} = \omega^2\)
    \(\frac{pdg_{1356}}{pdg_{5156}} = pdg_{2321}^{2}\)
LHS diff is -(A*k*pdg1467*cos(pdg2321*pdg9491) + pdg1356)/pdg5156 RHS diff is -pdg2321**2*(A*pdg1467*cos(pdg2321*pdg9491) + 1) 2148049269:
1931103031:
2148049269:
1931103031:
9 differentiate with respect to
  1. 7652131521; locally 4463004:
    \(\frac{dx}{dt} = -A \omega \sin (\omega t)\)
    \(\frac{d}{d pdg_{1467}} pdg_{4037} = - pdg_{2321} pdg_{9885} \sin{\left(pdg_{1467} pdg_{2321} \right)}\)
  1. 1451839362:
    \(t\)
    \(pdg_{1467}\)
  1. 5945893986; locally 4836115:
    \(\frac{d^2 x}{dt^2} = -A \omega^2 \cos(\omega t)\)
    \(\frac{d^{2} x}{dt^{2}} = - pdg_{2321}^{2} pdg_{9885} \cos{\left(pdg_{1467} pdg_{2321} \right)}\)
no check performed 7652131521:
5945893986:
7652131521:
5945893986:
5 divide both sides by
  1. 2334518266; locally 7273319:
    \(m a = -k x\)
    \(pdg_{5156} pdg_{9140} = - pdg_{1356} pdg_{4037}\)
  1. 3634715785:
    \(m\)
    \(pdg_{5156}\)
  1. 8655294002; locally 5403312:
    \(a = -\frac{k}{m}x\)
    \(pdg_{9140} = - \frac{pdg_{1356} pdg_{4037}}{pdg_{5156}}\)
valid 2334518266:
8655294002:
2334518266:
8655294002:
8 differentiate with respect to
  1. 5415824175; locally 2877569:
    \(x(t) = A \cos(\omega t)\)
    \(x{\left(pdg_{1467} \right)} = pdg_{9885} \cos{\left(pdg_{1467} pdg_{2321} \right)}\)
  1. 5846177002:
    \(t\)
    \(t\)
  1. 7652131521; locally 4463004:
    \(\frac{dx}{dt} = -A \omega \sin (\omega t)\)
    \(\frac{d}{d pdg_{1467}} pdg_{4037} = - pdg_{2321} pdg_{9885} \sin{\left(pdg_{1467} pdg_{2321} \right)}\)
no check performed 5415824175:
7652131521:
5415824175:
7652131521:
14 substitute RHS of expr 1 into expr 2
  1. 1784114349; locally 7243628:
    \(\sqrt{\frac{k}{m}} = \omega\)
    \(\sqrt{\frac{pdg_{1356}}{pdg_{5156}}} = pdg_{2321}\)
  2. 5415824175; locally 2877569:
    \(x(t) = A \cos(\omega t)\)
    \(x{\left(pdg_{1467} \right)} = pdg_{9885} \cos{\left(pdg_{1467} pdg_{2321} \right)}\)
  1. 6908055431; locally 5872898:
    \(x(t) = A \cos\left(\frac{k}{m} t\right)\)
    \(x{\left(pdg_{1467} \right)} = pdg_{9885} \cos{\left(\frac{k pdg_{1467}}{pdg_{5156}} \right)}\)
LHS diff is 0 RHS diff is pdg9885*(cos(pdg1467*sqrt(pdg1356/pdg5156)) - cos(k*pdg1467/pdg5156)) 1784114349:
5415824175:
6908055431: error for dim with 6908055431
 1784114349:
5415824175:
6908055431: N/A
15 declare final expr
  1. 6908055431; locally 5872898:
    \(x(t) = A \cos\left(\frac{k}{m} t\right)\)
    \(x{\left(pdg_{1467} \right)} = pdg_{9885} \cos{\left(\frac{k pdg_{1467}}{pdg_{5156}} \right)}\)
no validation is available for declarations 6908055431: error for dim with 6908055431
 6908055431: N/A
Physics Derivation Graph: Steps for equation of motion for a spring

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
1356 variable k
\(k\)		 real
  • mass: 1
  • time: -2
 linear stiffness, aka spring constant 7
4202 variable F
\(F\)		 ['real']
  • length: 1
  • mass: 1
  • time: -2
 force 21
1467 variable t
\(t\)		 ['real']
  • time: 1
 time 121
4183 variable F_{\rm{spring}}
\(F_{\rm{spring}}\)		 real
  • length: 1
  • mass: 1
  • time: -2
 force of a spring 1
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
9491 variable T
\(T\)		 ['real']
  • time: 1
 period 20
9140 variable a
\(a\)		 ['real']
  • length: 1
  • time: -2
 acceleration 31
5156 variable m
\(m\)		 ['real']
  • mass: 1
 mass 69
2321 variable \omega
\(\omega\)		 ['real']
  • time: -1
 angular frequency 26
9885 variable A
\(A\)		 real dimensionless amplitude 4
MESSAGE: