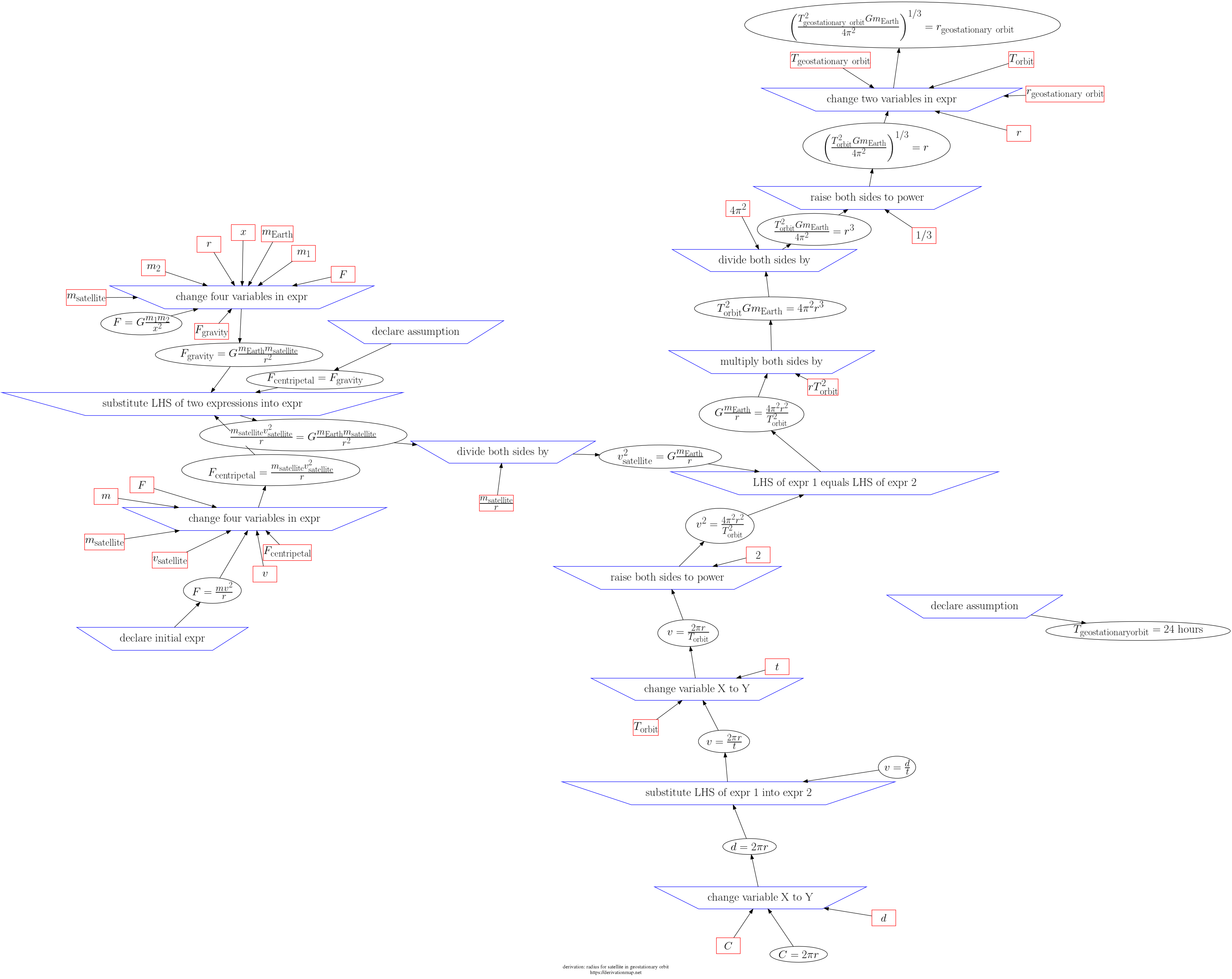
Physics Derivation Graph navigation Sign in

review derivation: radius for satellite in geostationary orbit

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
https://en.wikipedia.org/wiki/Geostationary_orbit#Derivation_of_geostationary_altitude

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
3 change four variables in expr
  1. 9226945488; locally 8242154:
    \(F = \frac{m v^2}{r}\)
    \(pdg_{4202} = \frac{pdg_{1357}^{2} pdg_{5156}}{pdg_{2530}}\)
  1. 5089196493:
    \(F\)
    \(pdg_{4202}\)
  2. 1333474099:
    \(F_{\rm centripetal}\)
    \(pdg_{1687}\)
  3. 3342155559:
    \(m\)
    \(pdg_{5156}\)
  4. 2114570475:
    \(m_{\rm satellite}\)
    \(pdg_{3569}\)
  5. 7912578203:
    \(v\)
    \(pdg_{1357}\)
  6. 9789485295:
    \(v_{\rm satellite}\)
    \(pdg_{4082}\)
  1. 4627284246; locally 6845877:
    \(F_{\rm centripetal} = \frac{m_{\rm satellite} v_{\rm satellite}^2}{r}\)
    \(pdg_{1687} = \frac{pdg_{3569} pdg_{4082}^{2}}{pdg_{2530}}\)
failed 9226945488:
4627284246:
9226945488:
4627284246:
12 multiply both sides by
  1. 3906710072; locally 2871066:
    \(G \frac{m_{\rm Earth}}{r} = \frac{4 \pi^2 r^2}{T_{\rm orbit}^2}\)
    \(\frac{pdg_{5458} pdg_{6277}}{pdg_{2530}} = \frac{4 pdg_{2530}^{2} pdg_{3141}^{2}}{pdg_{8762}^{2}}\)
  1. 6238632840:
    \(r T_{\rm orbit}^2\)
    \(pdg_{2530} pdg_{8762}^{2}\)
  1. 7010294143; locally 7188516:
    \(T_{\rm orbit}^2 G m_{\rm Earth} = 4 \pi^2 r^3\)
    \(pdg_{5458} pdg_{6277} pdg_{8762}^{2} = 4 pdg_{2530}^{3} pdg_{3141}^{2}\)
valid 3906710072:
7010294143:
3906710072:
7010294143:
14 raise both sides to power
  1. 4858693811; locally 6238570:
    \(\frac{T_{\rm orbit}^2 G m_{\rm Earth}}{4 \pi^2} = r^3\)
    \(\frac{pdg_{5458} pdg_{6277} pdg_{8762}^{2}}{4 pdg_{3141}^{2}} = pdg_{2530}^{3}\)
  1. 4319544433:
    \(1/3\)
    \(\frac{1}{3}\)
  1. 2617541067; locally 7139326:
    \(\left(\frac{T_{\rm orbit}^2 G m_{\rm Earth}}{4 \pi^2}\right)^{1/3} = r\)
    \(\frac{\sqrt[3]{2} \sqrt[3]{\frac{pdg_{5458} pdg_{6277} pdg_{8762}^{2}}{pdg_{3141}^{2}}}}{2} = pdg_{2530}\)
no check is performed 4858693811:
2617541067:
4858693811:
2617541067:
10 divide both sides by
  1. 4072200527; locally 4948724:
    \(\frac{m_{\rm satellite} v_{\rm satellite}^2}{r} = G \frac{m_{\rm Earth} m_{\rm satellite}}{r^2}\)
    \(\frac{pdg_{3569} pdg_{4082}^{2}}{pdg_{2530}} = \frac{pdg_{3569} pdg_{5458} pdg_{6277}}{pdg_{2530}^{2}}\)
  1. 5359471792:
    \(\frac{m_{\rm satellite}}{r}\)
    \(\frac{pdg_{3569}}{pdg_{2530}}\)
  1. 1994296484; locally 2009493:
    \(v_{\rm satellite}^2 = G \frac{m_{\rm Earth}}{r}\)
    \(pdg_{4082}^{2} = \frac{pdg_{5458} pdg_{6277}}{pdg_{2530}}\)
valid 4072200527:
1994296484:
4072200527:
1994296484:
16 change two variables in expr
  1. 2617541067; locally 7139326:
    \(\left(\frac{T_{\rm orbit}^2 G m_{\rm Earth}}{4 \pi^2}\right)^{1/3} = r\)
    \(\frac{\sqrt[3]{2} \sqrt[3]{\frac{pdg_{5458} pdg_{6277} pdg_{8762}^{2}}{pdg_{3141}^{2}}}}{2} = pdg_{2530}\)
  1. 3846345263:
    \(T_{\rm orbit}\)
    \(pdg_{8762}\)
  2. 5208737840:
    \(T_{\rm geostationary\ orbit}\)
    \(pdg_{5595}\)
  3. 5770088141:
    \(r\)
    \(pdg_{2530}\)
  4. 7053449926:
    \(r_{\rm geostationary\ orbit}\)
    \(pdg_{7110}\)
  1. 1559688463; locally 4507350:
    \(\left(\frac{T_{\rm geostationary\ orbit}^2 G m_{\rm Earth}}{4 \pi^2}\right)^{1/3} = r_{\rm geostationary\ orbit}\)
    \(\frac{\sqrt[3]{2} \sqrt[3]{\frac{pdg_{5458} pdg_{5595}^{2} pdg_{6277}}{pdg_{3141}^{2}}}}{2} = pdg_{7110}\)
valid 2617541067:
1559688463:
2617541067:
1559688463:
7 substitute LHS of expr 1 into expr 2
  1. 9262596735; locally 5369477:
    \(d = 2 \pi r\)
    \(pdg_{1943} = 2 pdg_{2530} pdg_{3141}\)
  2. 5426308937; locally 5114041:
    \(v = \frac{d}{t}\)
    \(pdg_{1357} = \frac{pdg_{1943}}{pdg_{1467}}\)
  1. 4245712581; locally 8090893:
    \(v = \frac{2 \pi r}{t}\)
    \(pdg_{1357} = \frac{2 pdg_{2530} pdg_{3141}}{pdg_{1467}}\)
valid 9262596735:
5426308937:
4245712581:
9262596735:
5426308937:
4245712581:
1 change four variables in expr
  1. 6935745841; locally 2820438:
    \(F = G \frac{m_1 m_2}{x^2}\)
    \(pdg_{4202} = \frac{pdg_{4851} pdg_{5022} pdg_{6277}}{pdg_{4037}^{2}}\)
  1. 3398368564:
    \(F\)
    \(pdg_{4202}\)
  2. 3594626260:
    \(F_{\rm gravity}\)
    \(pdg_{2867}\)
  3. 9794128647:
    \(m_1\)
    \(pdg_{5458}\)
  4. 4153613253:
    \(m_{\rm Earth}\)
    \(pdg_{5458}\)
  5. 3088463019:
    \(m_2\)
    \(pdg_{4851}\)
  6. 3486213448:
    \(m_{\rm satellite}\)
    \(pdg_{3569}\)
  7. 4830480629:
    \(x\)
    \(pdg_{4037}\)
  8. 7819443873:
    \(r\)
    \(pdg_{2530}\)
  1. 5563580265; locally 1917654:
    \(F_{\rm gravity} = G \frac{m_{\rm Earth} m_{\rm satellite}}{r^2}\)
    \(pdg_{2867} = \frac{pdg_{3569} pdg_{5458} pdg_{6277}}{pdg_{2530}^{2}}\)
LHS diff is 0 RHS diff is pdg3569*pdg6277*(pdg5022 - pdg5458)/pdg2530**2 6935745841:
5563580265:
6935745841:
5563580265:
8 change variable X to Y
  1. 4245712581; locally 8090893:
    \(v = \frac{2 \pi r}{t}\)
    \(pdg_{1357} = \frac{2 pdg_{2530} pdg_{3141}}{pdg_{1467}}\)
  1. 3722461713:
    \(t\)
    \(pdg_{1467}\)
  2. 9346215480:
    \(T_{\rm orbit}\)
    \(pdg_{8762}\)
  1. 3614055652; locally 2392562:
    \(v = \frac{2 \pi r}{T_{\rm orbit}}\)
    \(pdg_{1357} = \frac{2 pdg_{2530} pdg_{3141}}{pdg_{8762}}\)
valid 4245712581:
3614055652:
4245712581:
3614055652:
9 raise both sides to power
  1. 3614055652; locally 2392562:
    \(v = \frac{2 \pi r}{T_{\rm orbit}}\)
    \(pdg_{1357} = \frac{2 pdg_{2530} pdg_{3141}}{pdg_{8762}}\)
  1. 2754264786:
    \(2\)
    \(2\)
  1. 8059639673; locally 6390693:
    \(v^2 = \frac{4 \pi^2 r^2}{T_{\rm orbit}^2}\)
    \(pdg_{1357}^{2} = \frac{4 pdg_{2530}^{2} pdg_{3141}^{2}}{pdg_{8762}^{2}}\)
no check is performed 3614055652:
8059639673:
3614055652:
8059639673:
11 LHS of expr 1 equals LHS of expr 2
  1. 1994296484; locally 2009493:
    \(v_{\rm satellite}^2 = G \frac{m_{\rm Earth}}{r}\)
    \(pdg_{4082}^{2} = \frac{pdg_{5458} pdg_{6277}}{pdg_{2530}}\)
  2. 8059639673; locally 6390693:
    \(v^2 = \frac{4 \pi^2 r^2}{T_{\rm orbit}^2}\)
    \(pdg_{1357}^{2} = \frac{4 pdg_{2530}^{2} pdg_{3141}^{2}}{pdg_{8762}^{2}}\)
  1. 3906710072; locally 2871066:
    \(G \frac{m_{\rm Earth}}{r} = \frac{4 \pi^2 r^2}{T_{\rm orbit}^2}\)
    \(\frac{pdg_{5458} pdg_{6277}}{pdg_{2530}} = \frac{4 pdg_{2530}^{2} pdg_{3141}^{2}}{pdg_{8762}^{2}}\)
input diff is -pdg1357**2 + pdg4082**2 diff is 0 diff is 0 1994296484:
8059639673:
3906710072:
1994296484:
8059639673:
3906710072:
15 declare assumption
  1. 3920616792; locally 9978909:
    \(T_{\rm geostationary orbit} = 24\ {\rm hours}\)
    \(pdg_{5595}\)
no validation is available for declarations 3920616792:
3920616792:
5 substitute LHS of two expressions into expr
  1. 5563580265; locally 1917654:
    \(F_{\rm gravity} = G \frac{m_{\rm Earth} m_{\rm satellite}}{r^2}\)
    \(pdg_{2867} = \frac{pdg_{3569} pdg_{5458} pdg_{6277}}{pdg_{2530}^{2}}\)
  2. 4627284246; locally 6845877:
    \(F_{\rm centripetal} = \frac{m_{\rm satellite} v_{\rm satellite}^2}{r}\)
    \(pdg_{1687} = \frac{pdg_{3569} pdg_{4082}^{2}}{pdg_{2530}}\)
  3. 3176662571; locally 2154616:
    \(F_{\rm centripetal} = F_{\rm gravity}\)
    \(pdg_{2867} = pdg_{1687}\)
  1. 4072200527; locally 4948724:
    \(\frac{m_{\rm satellite} v_{\rm satellite}^2}{r} = G \frac{m_{\rm Earth} m_{\rm satellite}}{r^2}\)
    \(\frac{pdg_{3569} pdg_{4082}^{2}}{pdg_{2530}} = \frac{pdg_{3569} pdg_{5458} pdg_{6277}}{pdg_{2530}^{2}}\)
failed 5563580265:
4627284246:
3176662571: dimensions are consistent
4072200527:
5563580265:
4627284246:
3176662571: N/A
4072200527:
13 divide both sides by
  1. 7010294143; locally 7188516:
    \(T_{\rm orbit}^2 G m_{\rm Earth} = 4 \pi^2 r^3\)
    \(pdg_{5458} pdg_{6277} pdg_{8762}^{2} = 4 pdg_{2530}^{3} pdg_{3141}^{2}\)
  1. 7556442438:
    \(4 \pi^2\)
    \(4 pdg_{3141}^{2}\)
  1. 4858693811; locally 6238570:
    \(\frac{T_{\rm orbit}^2 G m_{\rm Earth}}{4 \pi^2} = r^3\)
    \(\frac{pdg_{5458} pdg_{6277} pdg_{8762}^{2}}{4 pdg_{3141}^{2}} = pdg_{2530}^{3}\)
valid 7010294143:
4858693811:
7010294143:
4858693811:
2 declare initial expr
  1. 9226945488; locally 8242154:
    \(F = \frac{m v^2}{r}\)
    \(pdg_{4202} = \frac{pdg_{1357}^{2} pdg_{5156}}{pdg_{2530}}\)
no validation is available for declarations 9226945488:
9226945488:
6 change variable X to Y
  1. 6785303857; locally 1115424:
    \(C = 2 \pi r\)
    \(pdg_{3034} = 2 pdg_{2530} pdg_{3141}\)
  1. 1823570358:
    \(C\)
    \(pdg_{3034}\)
  2. 3236313290:
    \(d\)
    \(pdg_{1943}\)
  1. 9262596735; locally 5369477:
    \(d = 2 \pi r\)
    \(pdg_{1943} = 2 pdg_{2530} pdg_{3141}\)
valid 6785303857:
9262596735:
6785303857:
9262596735:
4 declare assumption
  1. 3176662571; locally 2154616:
    \(F_{\rm centripetal} = F_{\rm gravity}\)
    \(pdg_{2867} = pdg_{1687}\)
no validation is available for declarations 3176662571: dimensions are consistent
 3176662571: N/A
Physics Derivation Graph: Steps for radius for satellite in geostationary orbit

Symbols for this derivation

See also all 215 symbols
symbol ID category latex scope dimension name value Used in derivations references
4202 variable F
\(F\)		 ['real']
  • length: 1
  • mass: 1
  • time: -2
 force 21
7110 variable r_{\rm geostationary\ orbit}
\(r_{\rm geostationary\ orbit}\)		 real
  • length: 1
 geostationary orbital radius 2
1467 variable t
\(t\)		 ['real']
  • time: 1
 time 120
5022 variable m_1
\(m_1\)		 real
  • mass: 1
 mass 18
1357 variable v
\(v\)		 ['real']
  • length: 1
  • time: -1
 velocity 80
2530 variable r
\(r\)		 ['real']
  • length: 1
 radius 34
3141 constant \pi
\(\pi\)		 ['real'] dimensionless pi 3.1415   dimensionless
 55
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
6277 constant G
\(G\)		 real
  • length: 3
  • mass: -1
  • time: -2
 gravitational constant 6.67430*10^{-11}   m^3 * kg^-1 * s^-2
 46
5458 constant m_{\rm Earth}
\(m_{\rm Earth}\)		 real
  • mass: 2
 mass of Earth 5.97237*10^24   kg
 34
3569 variable m_{\rm satellite}
\(m_{\rm satellite}\)		 real
  • mass: 1
 mass of satellite 6
4851 variable m_2
\(m_2\)		 real
  • mass: 1
 mass 17
8762 variable T_{\rm orbit}
\(T_{\rm orbit}\)		 real
  • time: 1
 orbital period 9
2867 variable F_{\rm gravity}
\(F_{\rm gravity}\)		 real
  • length: 1
  • mass: 1
  • time: -2
 force due to gravity 3
4082 variable v_{\rm satellite}
\(v_{\rm satellite}\)		 real
  • length: 1
  • time: -1
 velocity of satellite 4
1943 variable d
\(d\)		 ['real']
  • length: 1
 displacement 25
1687 variable F_{\rm centripetal}
\(F_{\rm centripetal}\)		 real
  • length: 1
  • mass: 1
  • time: -2
 centripetal force 3
5595 variable T_{\rm geostationary\ orbit}
\(T_{\rm geostationary\ orbit}\)		 real
  • time: 1
 geostationary orbital period 3
5156 variable m
\(m\)		 ['real']
  • mass: 1
 mass 57
3034 variable C
\(C\)		 ['real']
  • length: 1
 circumference 5
MESSAGES: