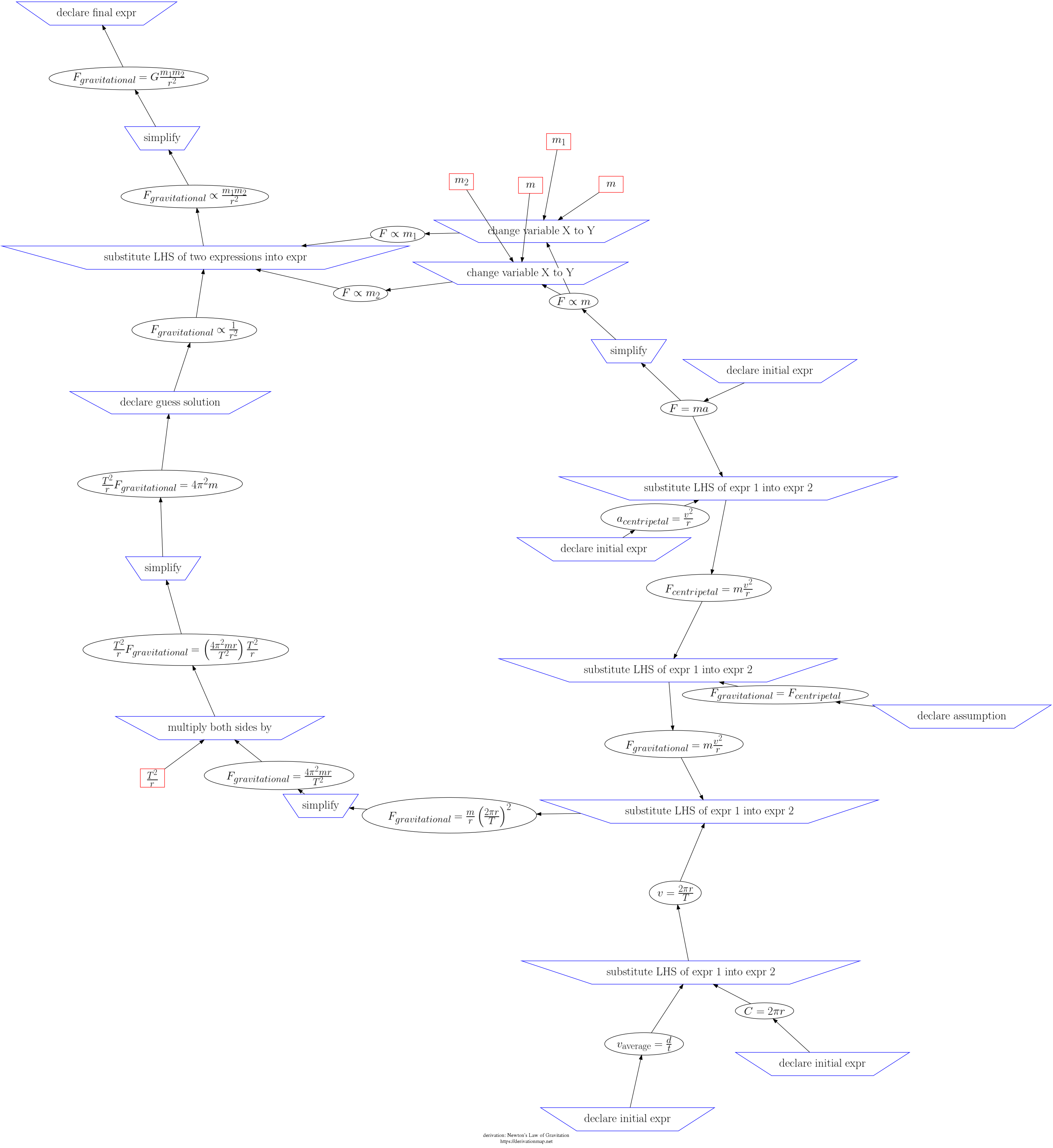
Physics Derivation Graph navigation Sign in

review derivation: Newton's Law of Gravitation

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
from https://www.youtube.com/watch?v=fJYdFIZlD8k

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
17 substitute LHS of two expressions into expr
  1. 4264859781; locally 8320848:
    \(F \propto m_1\)
    \(F pdg_{5022} propto\)
  2. 4490788873; locally 5440061:
    \(F \propto m_2\)
    \(F pdg_{4851} propto\)
  3. 1571582377; locally 6174613:
    \(F_{gravitational} \propto \frac{1}{r^2}\)
    \(pdg_{2867} = \frac{k}{pdg_{2530}^{2}}\)
  1. 3650814381; locally 1206000:
    \(F_{gravitational} \propto \frac{m_1 m_2}{r^2}\)
    \(\frac{pdg_{2867} pdg_{4851} pdg_{5022} propto}{pdg_{2530}^{2}}\)
Nothing to split 4264859781:
4490788873:
1571582377:
3650814381:
4264859781:
4490788873:
1571582377:
3650814381:
8 substitute LHS of expr 1 into expr 2
  1. 6026694087; locally 3755872:
    \(F_{centripetal} = m \frac{v^2}{r}\)
    \(pdg_{1687} = \frac{pdg_{5156} v^{2}}{pdg_{2530}}\)
  2. 4820320578; locally 5891249:
    \(F_{gravitational} = F_{centripetal}\)
    \(pdg_{2867} = pdg_{1687}\)
  1. 4267808354; locally 2239910:
    \(F_{gravitational} = m \frac{v^2}{r}\)
    \(pdg_{2867} = \frac{pdg_{1357}^{2} pdg_{5156}}{pdg_{2530}}\)
LHS diff is 0 RHS diff is pdg5156*(-pdg1357**2 + v**2)/pdg2530 6026694087:
4820320578:
4267808354:
6026694087:
4820320578:
4267808354:
10 declare initial expr
  1. 6785303857; locally 5154120:
    \(C = 2 \pi r\)
    \(pdg_{3034} = 2 pdg_{2530} pdg_{3141}\)
no validation is available for declarations 6785303857:
6785303857:
9 declare initial expr
  1. 3411994811; locally 9055493:
    \(v_{\rm average} = \frac{d}{t}\)
    \(pdg_{6709} = \frac{pdg_{1943}}{pdg_{1467}}\)
no validation is available for declarations 3411994811:
3411994811:
5 declare assumption
  1. 4820320578; locally 5891249:
    \(F_{gravitational} = F_{centripetal}\)
    \(pdg_{2867} = pdg_{1687}\)
no validation is available for declarations 4820320578:
4820320578:
19 declare final expr
  1. 1292735067; locally 8373934:
    \(F_{gravitational} = G \frac{m_1 m_2}{r^2}\)
    \(pdg_{2867} = \frac{pdg_{4851} pdg_{5022} pdg_{6277}}{pdg_{2530}^{2}}\)
no validation is available for declarations 1292735067:
1292735067:
7 substitute LHS of expr 1 into expr 2
  1. 8361238989; locally 6969192:
    \(a_{centripetal} = \frac{v^2}{r}\)
    \(a_{c*(e*(n*(t*(r*(i*(p*(e*(t*(a*l)))))))))} = \frac{pdg_{1357}^{2}}{pdg_{2530}}\)
  2. 5345738321; locally 2020292:
    \(F = m a\)
    \(pdg_{4202} = pdg_{5156} pdg_{9140}\)
  1. 6026694087; locally 3755872:
    \(F_{centripetal} = m \frac{v^2}{r}\)
    \(pdg_{1687} = \frac{pdg_{5156} v^{2}}{pdg_{2530}}\)
LHS diff is -pdg1687 + pdg4202 RHS diff is pdg5156*(pdg2530*pdg9140 - v**2)/pdg2530 8361238989:
5345738321: dimensions are consistent
6026694087:
8361238989:
5345738321: N/A
6026694087:
15 simplify
  1. 3004158505; locally 4470678:
    \(\frac{T^2}{r} F_{gravitational} = \left( \frac{4 \pi^2 m r}{T^2} \right)\frac{T^2}{r}\)
    \(\frac{pdg_{2867} pdg_{8762}^{2}}{pdg_{2530}} = 4 pdg_{3141}^{2} pdg_{5156}\)
  1. 3650370389; locally 7324555:
    \(\frac{T^2}{r} F_{gravitational} = 4 \pi^2 m\)
    \(\frac{pdg_{2867} pdg_{8762}^{2}}{pdg_{2530}} = 4 pdg_{3141}^{2} pdg_{5156}\)
valid 3004158505:
3650370389:
3004158505:
3650370389:
11 substitute LHS of expr 1 into expr 2
  1. 6785303857; locally 5154120:
    \(C = 2 \pi r\)
    \(pdg_{3034} = 2 pdg_{2530} pdg_{3141}\)
  2. 3411994811; locally 9055493:
    \(v_{\rm average} = \frac{d}{t}\)
    \(pdg_{6709} = \frac{pdg_{1943}}{pdg_{1467}}\)
  1. 5177311762; locally 7653722:
    \(v = \frac{2 \pi r}{T}\)
    \(pdg_{1357} = \frac{2 pdg_{2530} pdg_{3141}}{pdg_{8762}}\)
LHS diff is -pdg1357 + pdg6709 RHS diff is -2*pdg2530*pdg3141/pdg8762 + pdg1943/pdg1467 6785303857:
3411994811:
5177311762:
6785303857:
3411994811:
5177311762:
3 change variable X to Y
  1. 1848400430; locally 5546471:
    \(F \propto m\)
    \(F pdg_{5156} propto\)
  1. 3876446703:
    \(m\)
    \(pdg_{5156}\)
  2. 7905984866:
    \(m_1\)
    \(pdg_{5022}\)
  1. 4264859781; locally 8320848:
    \(F \propto m_1\)
    \(F pdg_{5022} propto\)
Nothing to split 1848400430: no LHS/RHS split
4264859781:
1848400430: N/A
4264859781:
18 simplify
  1. 3650814381; locally 1206000:
    \(F_{gravitational} \propto \frac{m_1 m_2}{r^2}\)
    \(\frac{pdg_{2867} pdg_{4851} pdg_{5022} propto}{pdg_{2530}^{2}}\)
  1. 1292735067; locally 8373934:
    \(F_{gravitational} = G \frac{m_1 m_2}{r^2}\)
    \(pdg_{2867} = \frac{pdg_{4851} pdg_{5022} pdg_{6277}}{pdg_{2530}^{2}}\)
Nothing to split 3650814381:
1292735067:
3650814381:
1292735067:
13 simplify
  1. 6268336290; locally 9170078:
    \(F_{gravitational} = \frac{m}{r}\left(\frac{2\pi r}{T}\right)^2\)
    \(pdg_{2867} = \frac{4 pdg_{2530} pdg_{3141}^{2} pdg_{4851}}{pdg_{8762}^{2}}\)
  1. 7672365885; locally 5175707:
    \(F_{gravitational} = \frac{4 \pi^2 m r}{T^2}\)
    \(pdg_{2867} = \frac{4 pdg_{2530} pdg_{3141}^{2} pdg_{4851}}{pdg_{8762}^{2}}\)
valid 6268336290:
7672365885:
6268336290:
7672365885:
14 multiply both sides by
  1. 7672365885; locally 5175707:
    \(F_{gravitational} = \frac{4 \pi^2 m r}{T^2}\)
    \(pdg_{2867} = \frac{4 pdg_{2530} pdg_{3141}^{2} pdg_{4851}}{pdg_{8762}^{2}}\)
  1. 3448601530:
    \(\frac{T^2}{r}\)
    \(\frac{pdg_{9491}^{2}}{pdg_{2530}}\)
  1. 3004158505; locally 4470678:
    \(\frac{T^2}{r} F_{gravitational} = \left( \frac{4 \pi^2 m r}{T^2} \right)\frac{T^2}{r}\)
    \(\frac{pdg_{2867} pdg_{8762}^{2}}{pdg_{2530}} = 4 pdg_{3141}^{2} pdg_{5156}\)
LHS diff is pdg2867*(-pdg8762**2 + pdg9491**2)/pdg2530 RHS diff is 4*pdg3141**2*(pdg4851*pdg9491**2 - pdg5156*pdg8762**2)/pdg8762**2 7672365885:
3004158505:
7672365885:
3004158505:
1 declare initial expr
  1. 5345738321; locally 2020292:
    \(F = m a\)
    \(pdg_{4202} = pdg_{5156} pdg_{9140}\)
no validation is available for declarations 5345738321: dimensions are consistent
 5345738321: N/A
6 declare initial expr
  1. 8361238989; locally 6969192:
    \(a_{centripetal} = \frac{v^2}{r}\)
    \(a_{c*(e*(n*(t*(r*(i*(p*(e*(t*(a*l)))))))))} = \frac{pdg_{1357}^{2}}{pdg_{2530}}\)
no validation is available for declarations 8361238989:
8361238989:
4 change variable X to Y
  1. 1848400430; locally 5546471:
    \(F \propto m\)
    \(F pdg_{5156} propto\)
  1. 2346952973:
    \(m\)
    \(pdg_{5156}\)
  2. 9594072504:
    \(m_2\)
    \(pdg_{4851}\)
  1. 4490788873; locally 5440061:
    \(F \propto m_2\)
    \(F pdg_{4851} propto\)
Nothing to split 1848400430: no LHS/RHS split
4490788873:
1848400430: N/A
4490788873:
12 substitute LHS of expr 1 into expr 2
  1. 5177311762; locally 7653722:
    \(v = \frac{2 \pi r}{T}\)
    \(pdg_{1357} = \frac{2 pdg_{2530} pdg_{3141}}{pdg_{8762}}\)
  2. 4267808354; locally 2239910:
    \(F_{gravitational} = m \frac{v^2}{r}\)
    \(pdg_{2867} = \frac{pdg_{1357}^{2} pdg_{5156}}{pdg_{2530}}\)
  1. 6268336290; locally 9170078:
    \(F_{gravitational} = \frac{m}{r}\left(\frac{2\pi r}{T}\right)^2\)
    \(pdg_{2867} = \frac{4 pdg_{2530} pdg_{3141}^{2} pdg_{4851}}{pdg_{8762}^{2}}\)
LHS diff is 0 RHS diff is 4*pdg2530*pdg3141**2*(-pdg4851 + pdg5156)/pdg8762**2 5177311762:
4267808354:
6268336290:
5177311762:
4267808354:
6268336290:
16 declare guess solution
  1. 3650370389; locally 7324555:
    \(\frac{T^2}{r} F_{gravitational} = 4 \pi^2 m\)
    \(\frac{pdg_{2867} pdg_{8762}^{2}}{pdg_{2530}} = 4 pdg_{3141}^{2} pdg_{5156}\)
  1. 1571582377; locally 6174613:
    \(F_{gravitational} \propto \frac{1}{r^2}\)
    \(pdg_{2867} = \frac{k}{pdg_{2530}^{2}}\)
no validation is available for declarations 3650370389:
1571582377:
3650370389:
1571582377:
this is a big leap of logic that is consistent with Kepler's third law of motion
2 simplify
  1. 5345738321; locally 2020292:
    \(F = m a\)
    \(pdg_{4202} = pdg_{5156} pdg_{9140}\)
  1. 1848400430; locally 5546471:
    \(F \propto m\)
    \(F pdg_{5156} propto\)
Nothing to split 5345738321: dimensions are consistent
1848400430: no LHS/RHS split
 5345738321: N/A
1848400430: N/A
Physics Derivation Graph: Steps for Newton's Law of Gravitation

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
4851 variable m_2
\(m_2\)		 real
  • mass: 1
 mass 31
3141 constant \pi
\(\pi\)		 ['real'] dimensionless pi 3.1415   dimensionless
 72
3034 variable C
\(C\)		 ['real']
  • length: 1
 circumference 5
1467 variable t
\(t\)		 ['real']
  • time: 1
 time 121
1943 variable d
\(d\)		 ['real']
  • length: 1
 displacement 25
4202 variable F
\(F\)		 ['real']
  • length: 1
  • mass: 1
  • time: -2
 force 21
1687 variable F_{\rm centripetal}
\(F_{\rm centripetal}\)		 real
  • length: 1
  • mass: 1
  • time: -2
 centripetal force 8
5022 variable m_1
\(m_1\)		 real
  • mass: 1
 mass 35
6277 constant G
\(G\)		 real
  • length: 3
  • mass: -1
  • time: -2
 gravitational constant 6.67430*10^{-11}   m^3 * kg^-1 * s^-2
 60
2530 variable r
\(r\)		 ['real']
  • length: 1
 radius 60
8762 variable T_{\rm orbit}
\(T_{\rm orbit}\)		 real
  • time: 1
 orbital period 14
2867 variable F_{\rm gravity}
\(F_{\rm gravity}\)		 real
  • length: 1
  • mass: 1
  • time: -2
 force due to gravity 12
6709 variable v_{\rm average}
\(v_{\rm average}\)		 real
  • length: 1
  • time: -1
 velocity average 2
9491 variable T
\(T\)		 ['real']
  • time: 1
 period 20
9140 variable a
\(a\)		 ['real']
  • length: 1
  • time: -2
 acceleration 31
1357 variable v
\(v\)		 ['real']
  • length: 1
  • time: -1
 velocity 83
5156 variable m
\(m\)		 ['real']
  • mass: 1
 mass 69
MESSAGE: