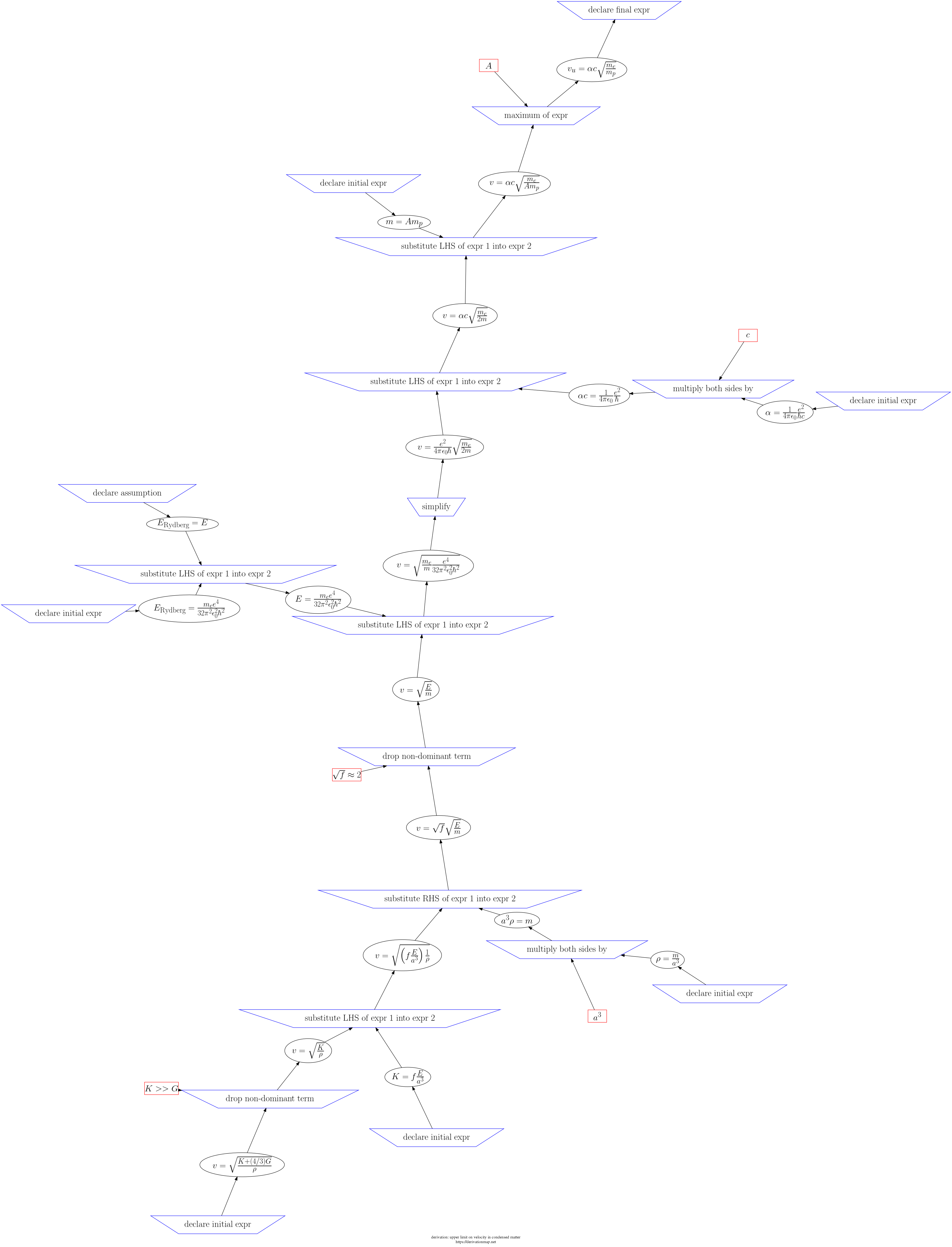
Physics Derivation Graph navigation Sign in

review derivation: upper limit on velocity in condensed matter

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
https://arxiv.org/pdf/2004.04818.pdf

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
11 declare initial expr
  1. 8106885760; locally 9431422:
    \(\alpha = \frac{1}{4 \pi \epsilon_0} \frac{e^2}{\hbar c}\)
    \(pdg_{1370} = \frac{pdg_{1999}^{2}}{4 pdg_{1054} pdg_{3141} pdg_{4567} pdg_{7940}}\)
no validation is available for declarations 8106885760:
8106885760:
12 multiply both sides by
  1. 8106885760; locally 9431422:
    \(\alpha = \frac{1}{4 \pi \epsilon_0} \frac{e^2}{\hbar c}\)
    \(pdg_{1370} = \frac{pdg_{1999}^{2}}{4 pdg_{1054} pdg_{3141} pdg_{4567} pdg_{7940}}\)
  1. 8857931498:
    \(c\)
    \(pdg_{4567}\)
  1. 5838268428; locally 6181437:
    \(\alpha c = \frac{1}{4 \pi \epsilon_0} \frac{e^2}{\hbar}\)
    \(pdg_{1370} pdg_{4567} = \frac{pdg_{1999}^{2}}{4 pdg_{1054} pdg_{3141} pdg_{7940}}\)
valid 8106885760:
5838268428: failed
 8106885760:
5838268428: N/A
9 declare initial expr
  1. 1556389363; locally 5961293:
    \(E_{\rm Rydberg} = \frac{ m_e e^4 }{ 32 \pi^2 \epsilon_0^2 \hbar^2}\)
    \(pdg_{9838} = \frac{pdg_{1999}^{4} pdg_{2515}}{32 pdg_{1054}^{2} pdg_{3141}^{2} pdg_{7940}^{2}}\)
no validation is available for declarations 1556389363:
1556389363:
7 substitute RHS of expr 1 into expr 2
  1. 8688588981; locally 7834577:
    \(a^3 \rho = m\)
    \(pdg_{3935} pdg_{5854}^{3} = pdg_{9863}\)
  2. 8090924099; locally 5077893:
    \(v = \sqrt{ \left( f\frac{E}{a^3} \right) \frac{1}{\rho} }\)
    \(pdg_{2077} = \sqrt{\frac{pdg_{2241} pdg_{6235}}{pdg_{3935} pdg_{5854}^{3}}}\)
  1. 7837519722; locally 5020923:
    \(v = \sqrt{f} \sqrt{\frac{E}{m}}\)
    \(pdg_{2077} = \sqrt{pdg_{6235}} \sqrt{\frac{pdg_{2241}}{pdg_{9863}}}\)
LHS diff is 0 RHS diff is -sqrt(pdg6235)*sqrt(pdg2241/pdg9863) + sqrt(pdg2241*pdg6235/(pdg3935*pdg5854**3)) 8688588981:
8090924099:
7837519722:
8688588981:
8090924099:
7837519722:
19 maximum of expr
  1. 2897612567; locally 8323044:
    \(v = \alpha c \sqrt{ \frac{m_e}{A m_p} }\)
    \(pdg_{2077} = pdg_{1370} pdg_{4567} \sqrt{\frac{pdg_{2515}}{pdg_{3285} pdg_{5916}}}\)
  1. 6259833695:
    \(A\)
    \(pdg_{3285}\)
  1. 7701249282; locally 9568206:
    \(v_u = \alpha c \sqrt{ \frac{m_e}{m_p} }\)
    \(pdg_{4635} = pdg_{1370} pdg_{4567} \sqrt{\frac{pdg_{2515}}{pdg_{5916}}}\)
no check performed 2897612567:
7701249282:
2897612567:
7701249282:
18 substitute LHS of expr 1 into expr 2
  1. 5646314683; locally 6979804:
    \(m = A m_p\)
    \(pdg_{9863} = pdg_{3285} pdg_{5916}\)
  2. 5789289057; locally 5883117:
    \(v = \alpha c \sqrt{ \frac{m_e}{2 m} }\)
    \(pdg_{2077} = \frac{\sqrt{2} pdg_{1370} pdg_{4567} \sqrt{\frac{pdg_{2515}}{pdg_{9863}}}}{2}\)
  1. 2897612567; locally 8323044:
    \(v = \alpha c \sqrt{ \frac{m_e}{A m_p} }\)
    \(pdg_{2077} = pdg_{1370} pdg_{4567} \sqrt{\frac{pdg_{2515}}{pdg_{3285} pdg_{5916}}}\)
LHS diff is 0 RHS diff is pdg1370*pdg4567*sqrt(pdg2515/(pdg3285*pdg5916))*(-2 + sqrt(2))/2 5646314683:
5789289057: error for dim with 5789289057
2897612567:
5646314683:
5789289057: N/A
2897612567:
20 declare final expr
  1. 7701249282; locally 9568206:
    \(v_u = \alpha c \sqrt{ \frac{m_e}{m_p} }\)
    \(pdg_{4635} = pdg_{1370} pdg_{4567} \sqrt{\frac{pdg_{2515}}{pdg_{5916}}}\)
no validation is available for declarations 7701249282:
7701249282:
13 substitute LHS of expr 1 into expr 2
  1. 4107032818; locally 6901924:
    \(E_{\rm Rydberg} = E\)
    \(pdg_{9838} = pdg_{2241}\)
  2. 1556389363; locally 5961293:
    \(E_{\rm Rydberg} = \frac{ m_e e^4 }{ 32 \pi^2 \epsilon_0^2 \hbar^2}\)
    \(pdg_{9838} = \frac{pdg_{1999}^{4} pdg_{2515}}{32 pdg_{1054}^{2} pdg_{3141}^{2} pdg_{7940}^{2}}\)
  1. 3291685884; locally 3642765:
    \(E = \frac{ m_e e^4 }{ 32 \pi^2 \epsilon_0^2 \hbar^2}\)
    \(pdg_{2241} = \frac{pdg_{1999}^{4} pdg_{2515}}{32 pdg_{1054}^{2} pdg_{3141}^{2} pdg_{7940}^{2}}\)
valid 4107032818:
1556389363:
3291685884:
4107032818:
1556389363:
3291685884:
10 declare assumption
  1. 4107032818; locally 6901924:
    \(E_{\rm Rydberg} = E\)
    \(pdg_{9838} = pdg_{2241}\)
no validation is available for declarations 4107032818:
4107032818:
15 simplify
  1. 3935058307; locally 2063484:
    \(v = \sqrt{ \frac{m_e}{m} \frac{e^4}{32 \pi^2 \epsilon_0^2 \hbar^2} }\)
    \(pdg_{2077} = \frac{\sqrt{2} \sqrt{\frac{pdg_{1999}^{4} pdg_{2515}}{pdg_{1054}^{2} pdg_{3141}^{2} pdg_{7940}^{2} pdg_{9863}}}}{8}\)
  1. 9640720571; locally 4586348:
    \(v = \frac{e^2}{4 \pi \epsilon_0 \hbar} \sqrt{\frac{m_e}{2 m}}\)
    \(pdg_{2077} = \frac{\sqrt{2} pdg_{1999}^{2} \sqrt{\frac{pdg_{2515}}{pdg_{9863}}}}{8 pdg_{1054} pdg_{3141} pdg_{7940}}\)
LHS diff is 0 RHS diff is sqrt(2)*(pdg1054*pdg3141*pdg7940*sqrt(pdg1999**4*pdg2515/(pdg1054**2*pdg3141**2*pdg7940**2*pdg9863)) - pdg1999**2*sqrt(pdg2515/pdg9863))/(8*pdg1054*pdg3141*pdg7940) 3935058307:
9640720571: failed
 3935058307:
9640720571: N/A
6 multiply both sides by
  1. 8908736791; locally 2438445:
    \(\rho = \frac{m}{a^3}\)
    \(pdg_{3935} = \frac{pdg_{9863}}{pdg_{5854}^{3}}\)
  1. 2397692197:
    \(a^3\)
    \(pdg_{5854}^{3}\)
  1. 8688588981; locally 7834577:
    \(a^3 \rho = m\)
    \(pdg_{3935} pdg_{5854}^{3} = pdg_{9863}\)
valid 8908736791:
8688588981:
8908736791:
8688588981:
2 declare initial expr
  1. 9376481176; locally 2178289:
    \(K = f \frac{E}{a^3}\)
    \(K = \frac{pdg_{2241} pdg_{6235}}{pdg_{5854}^{3}}\)
no validation is available for declarations 9376481176:
9376481176:
5 declare initial expr
  1. 8908736791; locally 2438445:
    \(\rho = \frac{m}{a^3}\)
    \(pdg_{3935} = \frac{pdg_{9863}}{pdg_{5854}^{3}}\)
no validation is available for declarations 8908736791:
8908736791:
4 substitute LHS of expr 1 into expr 2
  1. 9376481176; locally 2178289:
    \(K = f \frac{E}{a^3}\)
    \(K = \frac{pdg_{2241} pdg_{6235}}{pdg_{5854}^{3}}\)
  2. 6504442697; locally 9155336:
    \(v = \sqrt{ \frac{K}{\rho} }\)
    \(pdg_{2077} = \sqrt{\frac{K}{pdg_{3935}}}\)
  1. 8090924099; locally 5077893:
    \(v = \sqrt{ \left( f\frac{E}{a^3} \right) \frac{1}{\rho} }\)
    \(pdg_{2077} = \sqrt{\frac{pdg_{2241} pdg_{6235}}{pdg_{3935} pdg_{5854}^{3}}}\)
valid 9376481176:
6504442697:
8090924099:
9376481176:
6504442697:
8090924099:
1 declare initial expr
  1. 4560648264; locally 1719451:
    \(v = \sqrt{ \frac{K + (4/3) G}{\rho} }\)
    \(pdg_{2077} = \sqrt{\frac{pdg_{1466} + \frac{4 pdg_{3033}}{3}}{pdg_{3935}}}\)
no validation is available for declarations 4560648264:
4560648264:
14 substitute LHS of expr 1 into expr 2
  1. 3291685884; locally 3642765:
    \(E = \frac{ m_e e^4 }{ 32 \pi^2 \epsilon_0^2 \hbar^2}\)
    \(pdg_{2241} = \frac{pdg_{1999}^{4} pdg_{2515}}{32 pdg_{1054}^{2} pdg_{3141}^{2} pdg_{7940}^{2}}\)
  2. 9854442418; locally 4534919:
    \(v = \sqrt{\frac{E}{m}}\)
    \(pdg_{2077} = \sqrt{\frac{pdg_{2241}}{pdg_{9863}}}\)
  1. 3935058307; locally 2063484:
    \(v = \sqrt{ \frac{m_e}{m} \frac{e^4}{32 \pi^2 \epsilon_0^2 \hbar^2} }\)
    \(pdg_{2077} = \frac{\sqrt{2} \sqrt{\frac{pdg_{1999}^{4} pdg_{2515}}{pdg_{1054}^{2} pdg_{3141}^{2} pdg_{7940}^{2} pdg_{9863}}}}{8}\)
valid 3291685884:
9854442418:
3935058307:
3291685884:
9854442418:
3935058307:
17 declare initial expr
  1. 5646314683; locally 6979804:
    \(m = A m_p\)
    \(pdg_{9863} = pdg_{3285} pdg_{5916}\)
no validation is available for declarations 5646314683:
5646314683:
8 drop non-dominant term
  1. 7837519722; locally 5020923:
    \(v = \sqrt{f} \sqrt{\frac{E}{m}}\)
    \(pdg_{2077} = \sqrt{pdg_{6235}} \sqrt{\frac{pdg_{2241}}{pdg_{9863}}}\)
  1. 3685779219:
    \(\sqrt{f} \approx 2\)
    \(2 approx \sqrt{pdg_{6235}}\)
  1. 9854442418; locally 4534919:
    \(v = \sqrt{\frac{E}{m}}\)
    \(pdg_{2077} = \sqrt{\frac{pdg_{2241}}{pdg_{9863}}}\)
no check performed 7837519722:
9854442418:
7837519722:
9854442418:
3 drop non-dominant term
  1. 4560648264; locally 1719451:
    \(v = \sqrt{ \frac{K + (4/3) G}{\rho} }\)
    \(pdg_{2077} = \sqrt{\frac{pdg_{1466} + \frac{4 pdg_{3033}}{3}}{pdg_{3935}}}\)
  1. 9674924517:
    \(K >> G\)
    \(pdg_{1466} > pdg_{3033}\)
  1. 6504442697; locally 9155336:
    \(v = \sqrt{ \frac{K}{\rho} }\)
    \(pdg_{2077} = \sqrt{\frac{K}{pdg_{3935}}}\)
no check performed 4560648264:
6504442697:
4560648264:
6504442697:
16 substitute LHS of expr 1 into expr 2
  1. 5838268428; locally 6181437:
    \(\alpha c = \frac{1}{4 \pi \epsilon_0} \frac{e^2}{\hbar}\)
    \(pdg_{1370} pdg_{4567} = \frac{pdg_{1999}^{2}}{4 pdg_{1054} pdg_{3141} pdg_{7940}}\)
  2. 9640720571; locally 4586348:
    \(v = \frac{e^2}{4 \pi \epsilon_0 \hbar} \sqrt{\frac{m_e}{2 m}}\)
    \(pdg_{2077} = \frac{\sqrt{2} pdg_{1999}^{2} \sqrt{\frac{pdg_{2515}}{pdg_{9863}}}}{8 pdg_{1054} pdg_{3141} pdg_{7940}}\)
  1. 5789289057; locally 5883117:
    \(v = \alpha c \sqrt{ \frac{m_e}{2 m} }\)
    \(pdg_{2077} = \frac{\sqrt{2} pdg_{1370} pdg_{4567} \sqrt{\frac{pdg_{2515}}{pdg_{9863}}}}{2}\)
LHS diff is 0 RHS diff is sqrt(2)*sqrt(pdg2515/pdg9863)*(-4*pdg1054*pdg1370*pdg3141*pdg4567*pdg7940 + pdg1999**2)/(8*pdg1054*pdg3141*pdg7940) 5838268428: failed
9640720571: failed
5789289057: error for dim with 5789289057
 5838268428: N/A
9640720571: N/A
5789289057: N/A
Physics Derivation Graph: Steps for upper limit on velocity in condensed matter

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
9863 variable m
\(m\)		 real
  • mass: 1
 mass of atom or molecule 8
3935 variable \rho
\(\rho\)		 real
  • length: -3
  • mass: 1
 density 7
5916 constant m_p
\(m_p\)		 real
  • mass: 1
 mass of proton 1.67262192369E^{-27}   kg
 3
9838 variable E_{\rm Rydberg}
\(E_{\rm Rydberg}\)		 real dimensionless Rydberg energy 2
6235 variable f
\(f\)		 real dimensionless proportionality constant
  • str_note
5
3033 variable G
\(G\)		 real
  • length: -1
  • mass: 1
  • time: -2
 shear modulus 2
4635 constant v_u
\(v_u\)		 real
  • length: 1
  • time: -1
 upper limit on velocity in condensed matter 36100   m/s
 1
2515 constant m_e
\(m_e\)		 real
  • mass: 1
 mass of electron 9.1093837015E^{-31}   kg
 7
1466 variable K
\(K\)		 real
  • length: -1
  • mass: 1
  • time: -2
 bulk modulus 2
2077 variable v
\(v\)		 real
  • length: 1
  • time: -1
 longitudinal speed of sound in condensed matter 9
1999 constant e
\(e\)		 ['real']
  • electric charge: 1
 charge of an electron 1.602*10^{-19}   Columb
 6
4567 constant c
\(c\)		 ['real']
  • length: 1
  • time: -1
 speed of light in vacuum 299792458   meters/second
 32
3285 variable A
\(A\)		 real
  • mass: 1
 atomic mass 3
2241 variable E
\(E\)		 real dimensionless bonding energy
  • str_note
6
1370 constant \alpha
\(\alpha\)		 ['real'] dimensionless fine-structure constant 1/137.03599999   dimensionless
 5
7940 constant \epsilon_0
\(\epsilon_0\)		 real
  • electric charge: 2
  • length: -3
  • mass: -1
  • time: 2
 vacuum permittivity, permittivity of free space or electric constant or the distributed capacitance of the vacuum 8.8541878128E-{12}   F/m
 14
1054 constant \hbar
\(\hbar\)		 ['real']
  • length: 2
  • mass: 1
  • time: -1
 Reduced Planck's constant 1.0545718*10^{-34}   meter^2 kilogram second^-1
 33
5854 variable a
\(a\)		 real
  • length: 1
 atomic separation
  • str_note
5
3141 constant \pi
\(\pi\)		 ['real'] dimensionless pi 3.1415   dimensionless
 72
MESSAGES: