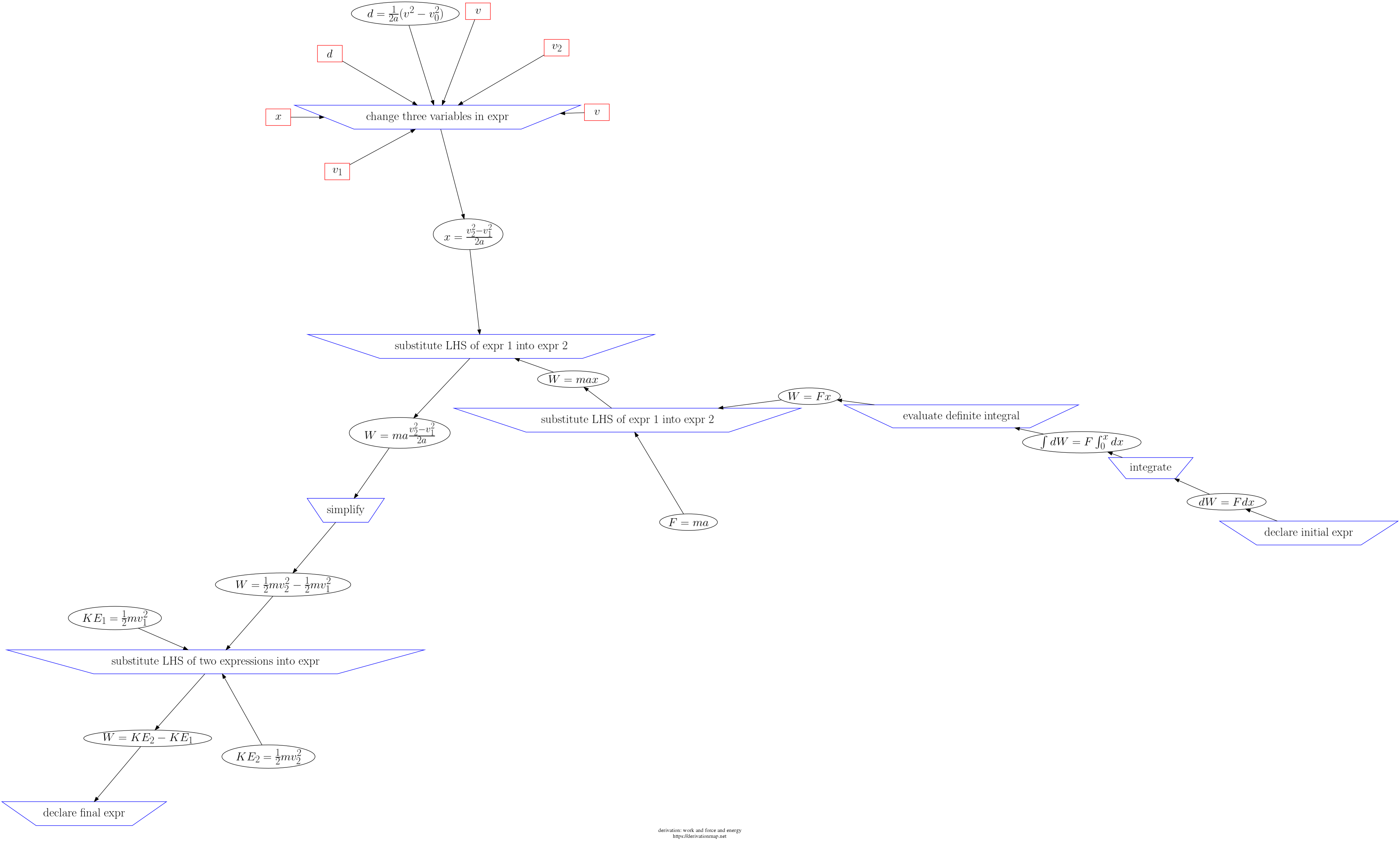
Physics Derivation Graph navigation Sign in

review derivation: work and force and energy

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
8 substitute LHS of two expressions into expr
  1. 7676652285; locally 8207477:
    \(KE_2 = \frac{1}{2} m v_2^2\)
    \(pdg_{1352} = \frac{pdg_{4770}^{2} pdg_{5156}}{2}\)
  2. 4928007622; locally 8883350:
    \(KE_1 = \frac{1}{2} m v_1^2\)
    \(pdg_{1955} = \frac{pdg_{2473}^{2} pdg_{5156}}{2}\)
  3. 4811121942; locally 4236963:
    \(W = \frac{1}{2} m v_2^2 - \frac{1}{2} m v_1^2\)
    \(pdg_{6789} = - \frac{pdg_{2473}^{2} pdg_{5156}}{2} + \frac{pdg_{4770}^{2} pdg_{5156}}{2}\)
  1. 3360172339; locally 4943050:
    \(W = KE_2 - KE_1\)
    \(pdg_{6789} = pdg_{1352} - pdg_{1955}\)
failed 7676652285:
4928007622:
4811121942:
3360172339:
7676652285:
4928007622:
4811121942:
3360172339:
2 integrate
  1. 1590774089; locally 2237799:
    \(dW = F dx\)
    \(pdg_{9398} = pdg_{4202} pdg_{9199}\)
  1. 5542528160; locally 2565189:
    \(\int dW = F \int_0^x dx\)
    \(\int 1\, dpdg_{6789} = pdg_{4202} \int\limits_{0}^{pdg_{4037}} 1\, dpdg_{4037}\)
no check performed 1590774089:
5542528160:
1590774089:
5542528160:
7 simplify
  1. 9413699705; locally 6760874:
    \(W = m a \frac{v_2^2 - v_1^2}{2 a}\)
    \(pdg_{6789} = pdg_{5156} \left(- \frac{pdg_{2473}^{2}}{2} + \frac{pdg_{4770}^{2}}{2}\right)\)
  1. 4811121942; locally 4236963:
    \(W = \frac{1}{2} m v_2^2 - \frac{1}{2} m v_1^2\)
    \(pdg_{6789} = - \frac{pdg_{2473}^{2} pdg_{5156}}{2} + \frac{pdg_{4770}^{2} pdg_{5156}}{2}\)
valid 9413699705: dimensions are consistent
4811121942:
9413699705: N/A
4811121942:
9 declare final expr
  1. 3360172339; locally 4943050:
    \(W = KE_2 - KE_1\)
    \(pdg_{6789} = pdg_{1352} - pdg_{1955}\)
no validation is available for declarations 3360172339:
3360172339:
3 evaluate definite integral
  1. 5542528160; locally 2565189:
    \(\int dW = F \int_0^x dx\)
    \(\int 1\, dpdg_{6789} = pdg_{4202} \int\limits_{0}^{pdg_{4037}} 1\, dpdg_{4037}\)
  1. 3512166162; locally 7362045:
    \(W = F x\)
    \(pdg_{6789} = pdg_{4037} pdg_{4202}\)
valid 5542528160:
3512166162:
5542528160:
3512166162:
1 declare initial expr
  1. 1590774089; locally 2237799:
    \(dW = F dx\)
    \(pdg_{9398} = pdg_{4202} pdg_{9199}\)
no validation is available for declarations 1590774089:
1590774089:
4 substitute LHS of expr 1 into expr 2
  1. 3512166162; locally 7362045:
    \(W = F x\)
    \(pdg_{6789} = pdg_{4037} pdg_{4202}\)
  2. 5345738321; locally 3086821:
    \(F = m a\)
    \(pdg_{4202} = pdg_{5156} pdg_{9140}\)
  1. 8953094349; locally 6167182:
    \(W = m a x\)
    \(pdg_{6789} = pdg_{4037} pdg_{5156} pdg_{9140}\)
LHS diff is pdg4202 - pdg6789 RHS diff is pdg5156*pdg9140*(1 - pdg4037) 3512166162:
5345738321:
8953094349: dimensions are consistent
 3512166162:
5345738321:
8953094349: N/A
5 change three variables in expr
  1. 5611024898; locally 4741344:
    \(d = \frac{1}{2 a} (v^2 - v_0^2)\)
    \(pdg_{1943} = \frac{pdg_{1357}^{2} - pdg_{5153}^{2}}{2 pdg_{9140}}\)
  1. 9623791270:
    \(d\)
    \(pdg_{4037}\)
  2. 8111389082:
    \(x\)
    \(pdg_{4037}\)
  3. 3652511721:
    \(v\)
    \(pdg_{1357}\)
  4. 6701855578:
    \(v_2\)
    \(pdg_{4770}\)
  5. 5398681502:
    \(v\)
    \(pdg_{1357}\)
  6. 3183197515:
    \(v_1\)
    \(pdg_{2473}\)
  1. 3253234559; locally 5997798:
    \(x = \frac{v_2^2 - v_1^2}{2 a}\)
    \(pdg_{4037} = \frac{- pdg_{2473}^{2} + pdg_{4770}^{2}}{2 pdg_{9140}}\)
LHS diff is pdg1943 - pdg4037 RHS diff is (pdg2473**2 - pdg5153**2)/(2*pdg9140) 5611024898:
3253234559: dimensions are consistent
 5611024898:
3253234559: N/A
6 substitute LHS of expr 1 into expr 2
  1. 3253234559; locally 5997798:
    \(x = \frac{v_2^2 - v_1^2}{2 a}\)
    \(pdg_{4037} = \frac{- pdg_{2473}^{2} + pdg_{4770}^{2}}{2 pdg_{9140}}\)
  2. 8953094349; locally 6167182:
    \(W = m a x\)
    \(pdg_{6789} = pdg_{4037} pdg_{5156} pdg_{9140}\)
  1. 9413699705; locally 6760874:
    \(W = m a \frac{v_2^2 - v_1^2}{2 a}\)
    \(pdg_{6789} = pdg_{5156} \left(- \frac{pdg_{2473}^{2}}{2} + \frac{pdg_{4770}^{2}}{2}\right)\)
valid 3253234559: dimensions are consistent
8953094349: dimensions are consistent
9413699705: dimensions are consistent
 3253234559: N/A
8953094349: N/A
9413699705: N/A
Physics Derivation Graph: Steps for work and force and energy

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
4202 variable F
\(F\)		 ['real']
  • length: 1
  • mass: 1
  • time: -2
 force 21
1357 variable v
\(v\)		 ['real']
  • length: 1
  • time: -1
 velocity 83
2473 variable v_1
\(v_1\)		 real
  • length: 1
  • time: -1
 velocity 1 14
9140 variable a
\(a\)		 ['real']
  • length: 1
  • time: -2
 acceleration 31
9398 variable dW
\(dW\)		 real
  • length: 2
  • mass: 1
  • time: -2
 differential work
  • str_note
2
4770 variable v_2
\(v_2\)		 real
  • length: 1
  • time: -1
 velocity 2 14
6789 variable W
\(W\)		 real
  • length: 2
  • mass: 1
  • time: -2
 work 10
1352 variable KE_2
\(KE_2\)		 real
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy 14
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
1955 variable KE_1
\(KE_1\)		 real
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy 17
5153 variable v_0
\(v_0\)		 ['real']
  • length: 1
  • time: -1
 initial velocity 44
1943 variable d
\(d\)		 ['real']
  • length: 1
 displacement 25
9199 variable dx
\(dx\)		 ['real']
  • length: 1
 15
5156 variable m
\(m\)		 ['real']
  • mass: 1
 mass 69
MESSAGES: