Physics Derivation Graph navigation Sign in

review derivation: projectile path in 2D is parabolic

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:
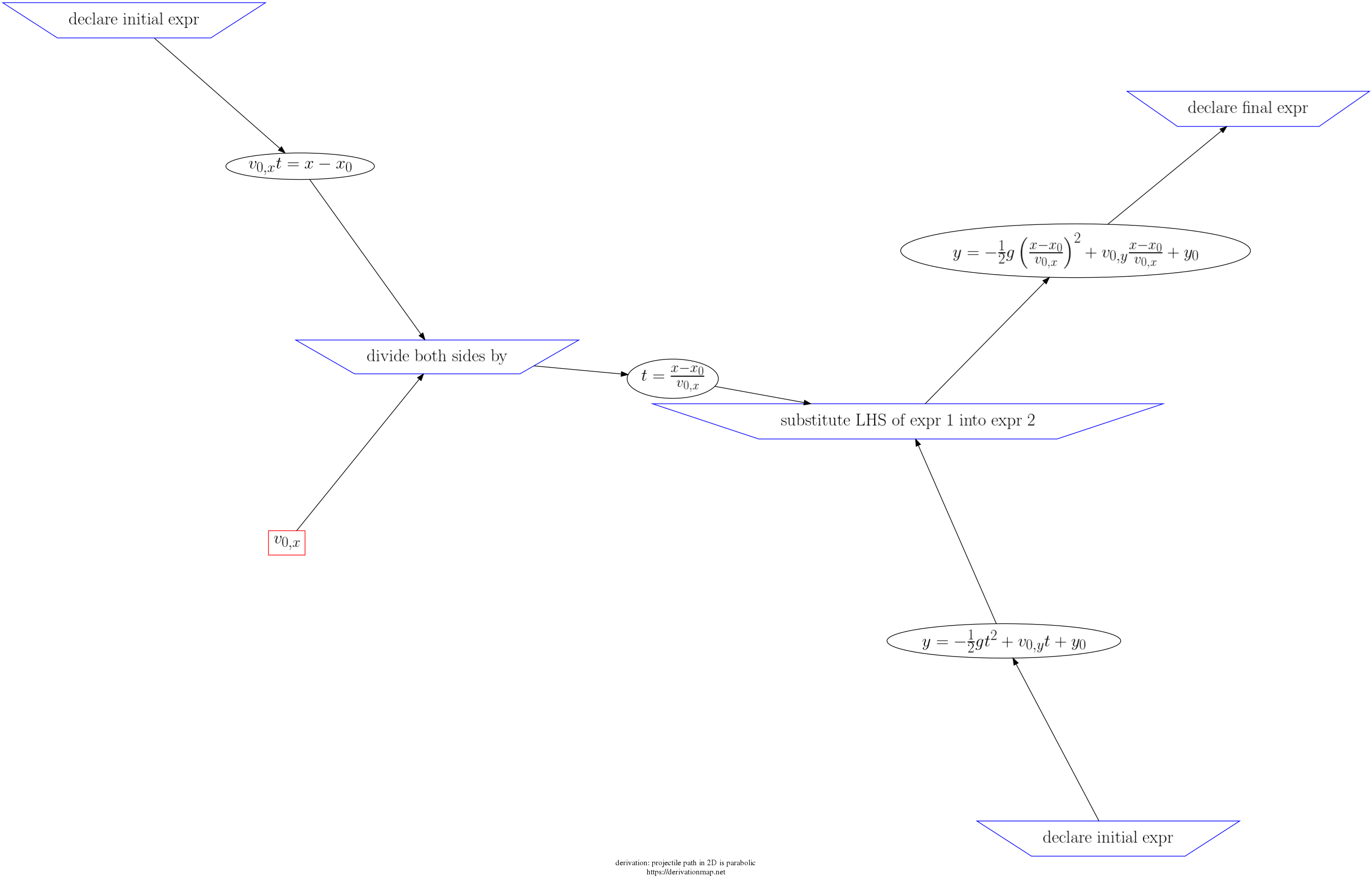
Using the 2D equations of motion, show that projectile path is second order polynomial of the form y = a x^2 + b x + c

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
4 substitute LHS of expr 1 into expr 2
  1. 3274926090; locally 8858248:
    \(t = \frac{x - x_0}{v_{0, x}}\)
    \(pdg_{1467} = \frac{- pdg_{1572} + pdg_{4037}}{pdg_{2958}}\)
  2. 1405465835; locally 5756391:
    \(y = - \frac{1}{2} g t^2 + v_{0, y} t + y_0\)
    \(pdg_{5647} = - \frac{pdg_{1467}^{2} pdg_{1649}}{2} + pdg_{1467} pdg_{9107} + pdg_{1469}\)
  1. 7354529102; locally 9683207:
    \(y = - \frac{1}{2} g \left( \frac{x - x_0}{v_{0, x}} \right)^2 + v_{0, y} \frac{x - x_0}{v_{0, x}} + y_0\)
    \(pdg_{5647} = pdg_{1469} - \frac{pdg_{1649}^{2} \left(- pdg_{1572} + pdg_{4037}\right)^{2}}{2 pdg_{2958}^{2}} + \frac{pdg_{9431} \left(- pdg_{1572} + pdg_{4037}\right)}{pdg_{2958}}\)
LHS diff is 0 RHS diff is (pdg1572 - pdg4037)*(pdg1649*(pdg1572 - pdg4037)*(pdg1649 - 1) + 2*pdg2958*(-pdg9107 + pdg9431))/(2*pdg2958**2) 3274926090:
1405465835: dimensions are consistent
7354529102:
3274926090:
1405465835: N/A
7354529102:
2 divide both sides by
  1. 9882526611; locally 4718749:
    \(v_{0, x} t = x - x_0\)
    \(pdg_{1467} pdg_{2958} = - pdg_{1572} + pdg_{4037}\)
  1. 6050070428:
    \(v_{0, x}\)
    \(pdg_{2958}\)
  1. 3274926090; locally 8858248:
    \(t = \frac{x - x_0}{v_{0, x}}\)
    \(pdg_{1467} = \frac{- pdg_{1572} + pdg_{4037}}{pdg_{2958}}\)
valid 9882526611:
3274926090:
9882526611:
3274926090:
5 declare final expr
  1. 7354529102; locally 9683207:
    \(y = - \frac{1}{2} g \left( \frac{x - x_0}{v_{0, x}} \right)^2 + v_{0, y} \frac{x - x_0}{v_{0, x}} + y_0\)
    \(pdg_{5647} = pdg_{1469} - \frac{pdg_{1649}^{2} \left(- pdg_{1572} + pdg_{4037}\right)^{2}}{2 pdg_{2958}^{2}} + \frac{pdg_{9431} \left(- pdg_{1572} + pdg_{4037}\right)}{pdg_{2958}}\)
no validation is available for declarations 7354529102:
7354529102:
expression is a second order polynomial; projecticle motion is parabolic
1 declare initial expr
  1. 9882526611; locally 4718749:
    \(v_{0, x} t = x - x_0\)
    \(pdg_{1467} pdg_{2958} = - pdg_{1572} + pdg_{4037}\)
no validation is available for declarations 9882526611:
9882526611:
3 declare initial expr
  1. 1405465835; locally 5756391:
    \(y = - \frac{1}{2} g t^2 + v_{0, y} t + y_0\)
    \(pdg_{5647} = - \frac{pdg_{1467}^{2} pdg_{1649}}{2} + pdg_{1467} pdg_{9107} + pdg_{1469}\)
no validation is available for declarations 1405465835: dimensions are consistent
 1405465835: N/A
Physics Derivation Graph: Steps for projectile path in 2D is parabolic

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
5647 variable y
\(y\)		 ['real']
  • length: 1
 position 14
1469 variable y_0
\(y_0\)		 ['real']
  • length: 1
 initial position 9
9107 variable v_y
\(v_y\)		 real
  • length: 1
  • time: -1
 velocity along y axis
  • str_note
7
1649 variable g
\(g\)		 ['real']
  • length: 1
  • time: -2
 acceleration due to gravity 27
1467 variable t
\(t\)		 ['real']
  • time: 1
 time 121
9431 variable v_{0, y}
\(v_{0, y}\)		 ['real']
  • length: 1
  • time: -1
 initial velocity along y axis 12
2958 variable v_{0, x}
\(v_{0, x}\)		 ['real']
  • length: 1
  • time: -1
 initial velocity along x axis 15
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
1572 variable x_0
\(x_0\)		 ['real']
  • length: 1
 initial position 11
MESSAGE: