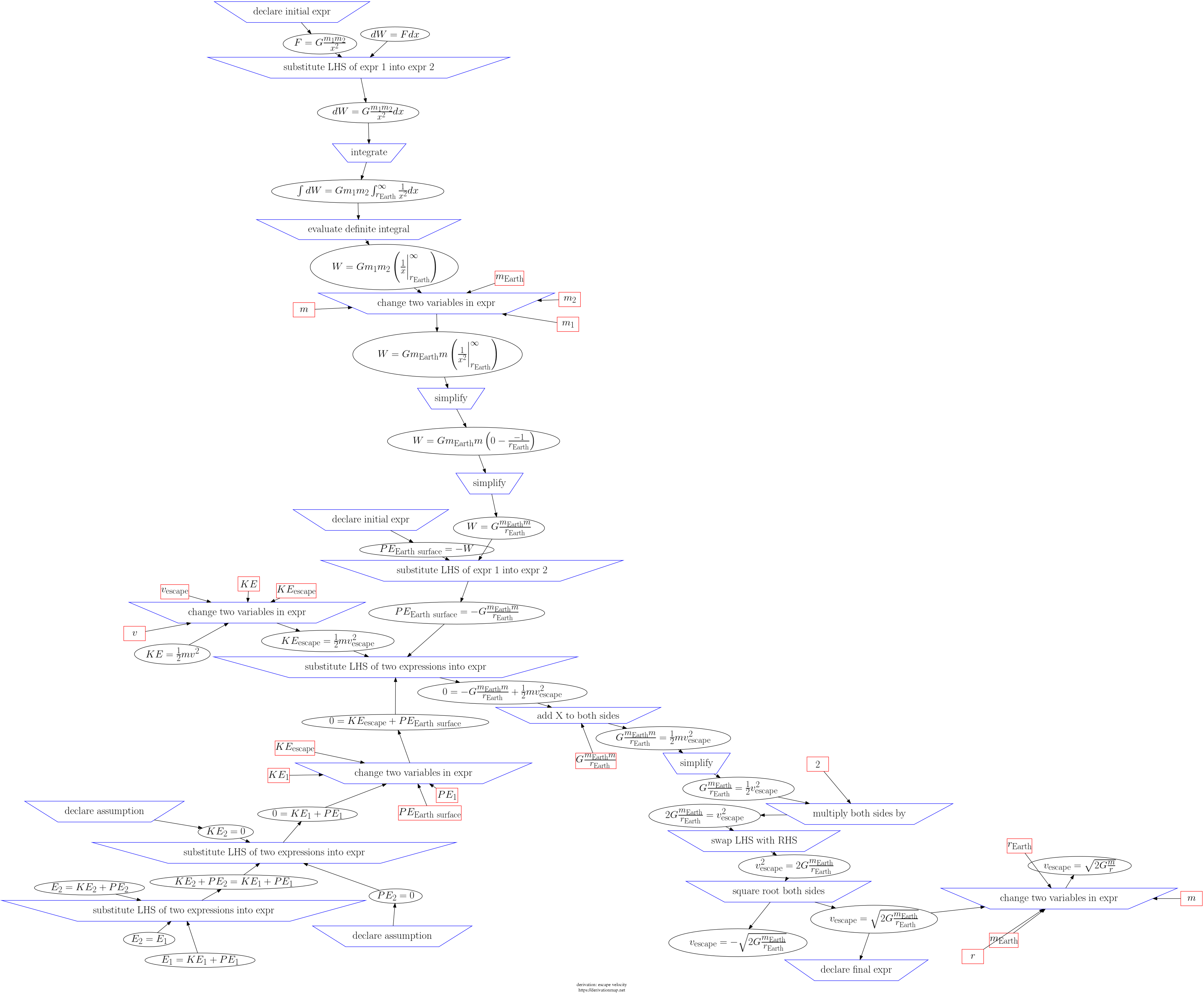
Physics Derivation Graph navigation Sign in

review derivation: escape velocity

This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Notes for this derivation:

Options
Alternate views of this derivation:
Edit this content:    

To edit a step, click on the number in the "Index" column in the table below

Clicking on the step index will take you to the page where you can edit that step.

Index Inference Rule Input latex Feeds latex Output latex step validity dimension check unit check notes
20 swap LHS with RHS
  1. 2977457786; locally 3358651:
    \(2 G \frac{m_{\rm Earth}}{r_{\rm Earth}} = v_{\rm escape}^2\)
    \(\frac{2 pdg_{5458} pdg_{6277}}{pdg_{3236}} = pdg_{8656}^{2}\)
  1. 9412953728; locally 3908344:
    \(v_{\rm escape}^2 = 2 G \frac{m_{\rm Earth}}{r_{\rm Earth}}\)
    \(pdg_{8656}^{2} = \frac{2 pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
valid 2977457786:
9412953728:
2977457786:
9412953728:
8 substitute LHS of two expressions into expr
  1. 4303372136; locally 6310702:
    \(E_1 = KE_1 + PE_1\)
    \(pdg_{5579} = pdg_{1955} + pdg_{4093}\)
  2. 7875206161; locally 5160388:
    \(E_2 = KE_2 + PE_2\)
    \(pdg_{4550} = pdg_{1352} + pdg_{8849}\)
  3. 8558338742; locally 6330719:
    \(E_2 = E_1\)
    \(pdg_{4550} = pdg_{5579}\)
  1. 8960645192; locally 4840471:
    \(KE_2 + PE_2 = KE_1 + PE_1\)
    \(pdg_{1552} + pdg_{8849} = pdg_{1955} + pdg_{4093}\)
failed 4303372136:
7875206161:
8558338742:
8960645192:
4303372136:
7875206161:
8558338742:
8960645192:
9 declare assumption
  1. 2267521164; locally 7682341:
    \(PE_2 = 0\)
    \(pdg_{8849} = 0\)
no validation is available for declarations 2267521164:
2267521164:
13 declare initial expr
  1. 7573835180; locally 6773616:
    \(PE_{\rm Earth\ surface} = -W\)
    \(pdg_{6431} = - pdg_{6789}\)
no validation is available for declarations 7573835180:
7573835180:
19 multiply both sides by
  1. 1143343287; locally 7567097:
    \(G \frac{m_{\rm Earth}}{r_{\rm Earth}} = \frac{1}{2} v_{\rm escape}^2\)
    \(\frac{pdg_{5458} pdg_{6277}}{pdg_{3236}} = \frac{pdg_{8656}^{2}}{2}\)
  1. 5775658332:
    \(2\)
    \(2\)
  1. 2977457786; locally 3358651:
    \(2 G \frac{m_{\rm Earth}}{r_{\rm Earth}} = v_{\rm escape}^2\)
    \(\frac{2 pdg_{5458} pdg_{6277}}{pdg_{3236}} = pdg_{8656}^{2}\)
valid 1143343287:
2977457786:
1143343287:
2977457786:
4 evaluate definite integral
  1. 4447113478; locally 4803506:
    \(\int dW = G m_1 m_2 \int_{ r_{\rm Earth} }^{\infty} \frac{1}{x^2} dx\)
    \(\int 1\, dpdg_{6789} = pdg_{4851} pdg_{5022} pdg_{6277} \int\limits_{pdg_{3236}}^{infty} \frac{1}{pdg_{4037}^{2}}\, dpdg_{4037}\)
  1. 5732331610; locally 1089445:
    \(W = G m_1 m_2 \left( \frac{1}{x} \bigg\rvert_{ r_{\rm Earth} }^{\infty} \right)\)
    \(pdg_{6277}\)
Nothing to split 4447113478:
5732331610:
4447113478:
5732331610:
7 simplify
  1. 5978756813; locally 2190752:
    \(W = G m_{\rm Earth} m \left( 0 - \frac{-1}{ r_{\rm Earth}} \right)\)
    \(pdg_{6789} = \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
  1. 7749253510; locally 2238158:
    \(W = G \frac{m_{\rm Earth} m }{ r_{\rm Earth}}\)
    \(pdg_{6789} = \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
valid 5978756813:
7749253510:
5978756813:
7749253510:
22 declare final expr
  1. 1330874553; locally 6389964:
    \(v_{\rm escape} = \sqrt{2 G \frac{m_{\rm Earth}}{r_{\rm Earth}}}\)
    \(pdg_{8656} = \sqrt{2} \sqrt{\frac{pdg_{5458} pdg_{6277}}{pdg_{3236}}}\)
no validation is available for declarations 1330874553:
1330874553:
23 change two variables in expr
  1. 1330874553; locally 6389964:
    \(v_{\rm escape} = \sqrt{2 G \frac{m_{\rm Earth}}{r_{\rm Earth}}}\)
    \(pdg_{8656} = \sqrt{2} \sqrt{\frac{pdg_{5458} pdg_{6277}}{pdg_{3236}}}\)
  1. 2674546234:
    \(m_{\rm Earth}\)
    \(pdg_{5458}\)
  2. 2135482543:
    \(m\)
    \(pdg_{5156}\)
  3. 2396787389:
    \(r_{\rm Earth}\)
    \(pdg_{3236}\)
  4. 8020058613:
    \(r\)
    \(pdg_{2530}\)
  1. 5404822208; locally 1619188:
    \(v_{\rm escape} = \sqrt{2 G \frac{m}{r}}\)
    \(pdg_{8656} = \sqrt{2} \sqrt{\frac{pdg_{5156} pdg_{6277}}{pdg_{2530}}}\)
valid 1330874553:
5404822208:
1330874553:
5404822208:
replaced Earth-specific variables
21 square root both sides
  1. 9412953728; locally 3908344:
    \(v_{\rm escape}^2 = 2 G \frac{m_{\rm Earth}}{r_{\rm Earth}}\)
    \(pdg_{8656}^{2} = \frac{2 pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
  1. 1330874553; locally 6389964:
    \(v_{\rm escape} = \sqrt{2 G \frac{m_{\rm Earth}}{r_{\rm Earth}}}\)
    \(pdg_{8656} = \sqrt{2} \sqrt{\frac{pdg_{5458} pdg_{6277}}{pdg_{3236}}}\)
  2. 2750380042; locally 8779043:
    \(v_{\rm escape} = -\sqrt{2 G \frac{m_{\rm Earth}}{r_{\rm Earth}}}\)
    \(pdg_{8656} = - \sqrt{2} \sqrt{\frac{pdg_{5458} pdg_{6277}}{pdg_{3236}}}\)
no check performed 9412953728:
1330874553:
2750380042:
9412953728:
1330874553:
2750380042:
2 substitute LHS of expr 1 into expr 2
  1. 6935745841; locally 3279838:
    \(F = G \frac{m_1 m_2}{x^2}\)
    \(pdg_{4202} = \frac{pdg_{4851} pdg_{5022} pdg_{6277}}{pdg_{4037}^{2}}\)
  2. 1590774089; locally 2123766:
    \(dW = F dx\)
    \(pdg_{9398} = pdg_{4202} pdg_{9199}\)
  1. 8604483515; locally 3686928:
    \(dW = G \frac{m_1 m_2}{x^2} dx\)
    \(pdg_{9398} = \frac{pdg_{4851} pdg_{5022} pdg_{6277} pdg_{9199}}{pdg_{4037}^{2}}\)
valid 6935745841:
1590774089:
8604483515:
6935745841:
1590774089:
8604483515:
18 simplify
  1. 9703482302; locally 6523887:
    \(G \frac{m_{\rm Earth} m}{r_{\rm Earth}} = \frac{1}{2} m v_{\rm escape}^2\)
    \(\frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}} = \frac{pdg_{5156} pdg_{8656}^{2}}{2}\)
  1. 1143343287; locally 7567097:
    \(G \frac{m_{\rm Earth}}{r_{\rm Earth}} = \frac{1}{2} v_{\rm escape}^2\)
    \(\frac{pdg_{5458} pdg_{6277}}{pdg_{3236}} = \frac{pdg_{8656}^{2}}{2}\)
LHS diff is pdg5458*pdg6277*(pdg5156 - 1)/pdg3236 RHS diff is pdg8656**2*(pdg5156 - 1)/2 9703482302:
1143343287:
9703482302:
1143343287:
3 integrate
  1. 8604483515; locally 3686928:
    \(dW = G \frac{m_1 m_2}{x^2} dx\)
    \(pdg_{9398} = \frac{pdg_{4851} pdg_{5022} pdg_{6277} pdg_{9199}}{pdg_{4037}^{2}}\)
  1. 4447113478; locally 4803506:
    \(\int dW = G m_1 m_2 \int_{ r_{\rm Earth} }^{\infty} \frac{1}{x^2} dx\)
    \(\int 1\, dpdg_{6789} = pdg_{4851} pdg_{5022} pdg_{6277} \int\limits_{pdg_{3236}}^{infty} \frac{1}{pdg_{4037}^{2}}\, dpdg_{4037}\)
no check performed 8604483515:
4447113478:
8604483515:
4447113478:
14 substitute LHS of expr 1 into expr 2
  1. 7749253510; locally 2238158:
    \(W = G \frac{m_{\rm Earth} m }{ r_{\rm Earth}}\)
    \(pdg_{6789} = \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
  2. 7573835180; locally 6773616:
    \(PE_{\rm Earth\ surface} = -W\)
    \(pdg_{6431} = - pdg_{6789}\)
  1. 3846041519; locally 9437784:
    \(PE_{\rm Earth\ surface} = -G \frac{m_{\rm Earth} m}{r_{\rm Earth}}\)
    \(pdg_{6431} = - \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
valid 7749253510:
7573835180:
3846041519:
7749253510:
7573835180:
3846041519:
1 declare initial expr
  1. 6935745841; locally 3279838:
    \(F = G \frac{m_1 m_2}{x^2}\)
    \(pdg_{4202} = \frac{pdg_{4851} pdg_{5022} pdg_{6277}}{pdg_{4037}^{2}}\)
no validation is available for declarations 6935745841:
6935745841:
10 declare assumption
  1. 1840080113; locally 9324316:
    \(KE_2 = 0\)
    \(pdg_{1552} = 0\)
no validation is available for declarations 1840080113:
1840080113:
11 substitute LHS of two expressions into expr
  1. 2267521164; locally 7682341:
    \(PE_2 = 0\)
    \(pdg_{8849} = 0\)
  2. 1840080113; locally 9324316:
    \(KE_2 = 0\)
    \(pdg_{1552} = 0\)
  3. 8960645192; locally 4840471:
    \(KE_2 + PE_2 = KE_1 + PE_1\)
    \(pdg_{1552} + pdg_{8849} = pdg_{1955} + pdg_{4093}\)
  1. 9749777192; locally 8369684:
    \(0 = KE_1 + PE_1\)
    \(0 = pdg_{1955} + pdg_{4093}\)
failed 2267521164:
1840080113:
8960645192:
9749777192: error for dim with 9749777192
 2267521164:
1840080113:
8960645192:
9749777192: N/A
5 change two variables in expr
  1. 5732331610; locally 1089445:
    \(W = G m_1 m_2 \left( \frac{1}{x} \bigg\rvert_{ r_{\rm Earth} }^{\infty} \right)\)
    \(pdg_{6277}\)
  1. 1413137236:
    \(m_1\)
    \(pdg_{5022}\)
  2. 9072369552:
    \(m_{\rm Earth}\)
    \(pdg_{5458}\)
  3. 2764966428:
    \(m_2\)
    \(pdg_{4851}\)
  4. 7140470627:
    \(m\)
    \(pdg_{5156}\)
  1. 6131764194; locally 2341415:
    \(W = G m_{\rm Earth} m \left( \frac{1}{x^2} \bigg\rvert_{ r_{\rm Earth} }^{\infty} \right)\)
    \(W = \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{4037}^{2}}\)
Nothing to split 5732331610:
6131764194:
5732331610:
6131764194:
16 substitute LHS of two expressions into expr
  1. 6870322215; locally 5106827:
    \(KE_{\rm escape} = \frac{1}{2} m v_{\rm escape}^2\)
    \(pdg_{5332} = \frac{pdg_{5156} pdg_{8656}^{2}}{2}\)
  2. 3846041519; locally 9437784:
    \(PE_{\rm Earth\ surface} = -G \frac{m_{\rm Earth} m}{r_{\rm Earth}}\)
    \(pdg_{6431} = - \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
  3. 2503972039; locally 9967559:
    \(0 = KE_{\rm escape} + PE_{\rm Earth\ surface}\)
    \(0 = pdg_{5332} + pdg_{6431}\)
  1. 2042298788; locally 3493665:
    \(0 = -G \frac{m_{\rm Earth} m}{r_{\rm Earth}} + \frac{1}{2} m v_{\rm escape}^2\)
    \(0 = \frac{pdg_{5156} pdg_{8656}^{2}}{2} - \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
failed 6870322215:
3846041519:
2503972039: error for dim with 2503972039
2042298788:
6870322215:
3846041519:
2503972039: N/A
2042298788:
15 change two variables in expr
  1. 8357234146; locally 3778087:
    \(KE = \frac{1}{2} m v^2\)
    \(pdg_{4929} = \frac{pdg_{1357}^{2} pdg_{5156}}{2}\)
  1. 5021965469:
    \(KE\)
    \(pdg_{4929}\)
  2. 9370882921:
    \(KE_{\rm escape}\)
    \(pdg_{5332}\)
  3. 6681646197:
    \(v\)
    \(pdg_{1357}\)
  4. 6498985149:
    \(v_{\rm escape}\)
    \(pdg_{8656}\)
  1. 6870322215; locally 5106827:
    \(KE_{\rm escape} = \frac{1}{2} m v_{\rm escape}^2\)
    \(pdg_{5332} = \frac{pdg_{5156} pdg_{8656}^{2}}{2}\)
valid 8357234146:
6870322215:
8357234146:
6870322215:
17 add X to both sides
  1. 2042298788; locally 3493665:
    \(0 = -G \frac{m_{\rm Earth} m}{r_{\rm Earth}} + \frac{1}{2} m v_{\rm escape}^2\)
    \(0 = \frac{pdg_{5156} pdg_{8656}^{2}}{2} - \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
  1. 5050429607:
    \(G \frac{m_{\rm Earth} m}{r_{\rm Earth}}\)
    \(\frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
  1. 9703482302; locally 6523887:
    \(G \frac{m_{\rm Earth} m}{r_{\rm Earth}} = \frac{1}{2} m v_{\rm escape}^2\)
    \(\frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}} = \frac{pdg_{5156} pdg_{8656}^{2}}{2}\)
valid 2042298788:
9703482302:
2042298788:
9703482302:
6 simplify
  1. 6131764194; locally 2341415:
    \(W = G m_{\rm Earth} m \left( \frac{1}{x^2} \bigg\rvert_{ r_{\rm Earth} }^{\infty} \right)\)
    \(W = \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{4037}^{2}}\)
  1. 5978756813; locally 2190752:
    \(W = G m_{\rm Earth} m \left( 0 - \frac{-1}{ r_{\rm Earth}} \right)\)
    \(pdg_{6789} = \frac{pdg_{5156} pdg_{5458} pdg_{6277}}{pdg_{3236}}\)
LHS diff is W - pdg6789 RHS diff is pdg5156*pdg5458*pdg6277*(pdg3236 - pdg4037**2)/(pdg3236*pdg4037**2) 6131764194:
5978756813:
6131764194:
5978756813:
12 change two variables in expr
  1. 9749777192; locally 8369684:
    \(0 = KE_1 + PE_1\)
    \(0 = pdg_{1955} + pdg_{4093}\)
  1. 5591692598:
    \(KE_1\)
    \(pdg_{1955}\)
  2. 8416464049:
    \(KE_{\rm escape}\)
    \(pdg_{5332}\)
  3. 6158970683:
    \(PE_1\)
    \(pdg_{4093}\)
  4. 8871333437:
    \(PE_{\rm Earth\ surface}\)
    \(pdg_{6431}\)
  1. 2503972039; locally 9967559:
    \(0 = KE_{\rm escape} + PE_{\rm Earth\ surface}\)
    \(0 = pdg_{5332} + pdg_{6431}\)
valid 9749777192: error for dim with 9749777192
2503972039: error for dim with 2503972039
 9749777192: N/A
2503972039: N/A
Physics Derivation Graph: Steps for escape velocity

Symbols for this derivation

See also all 227 symbols
symbol ID category latex scope dimension name value Used in derivations references
5332 variable KE_{\rm escape}
\(KE_{\rm escape}\)		 real
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy of escape velocity
  • str_note
4
4037 variable x
\(x\)		 ['real']
  • length: 1
 position 53
3236 constant r_{\rm Earth}
\(r_{\rm Earth}\)		 real
  • length: 1
 radius of Earth 6.3781*10^{6}   m
 21
4202 variable F
\(F\)		 ['real']
  • length: 1
  • mass: 1
  • time: -2
 force 21
5458 constant m_{\rm Earth}
\(m_{\rm Earth}\)		 real
  • mass: 2
 mass of Earth 5.97237*10^24   kg
 34
5022 variable m_1
\(m_1\)		 real
  • mass: 1
 mass 35
4929 variable KE
\(KE\)		 ['real']
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy 7
6789 variable W
\(W\)		 real
  • length: 2
  • mass: 1
  • time: -2
 work 10
6431 variable PE_{\rm Earth\ surface}
\(PE_{\rm Earth\ surface}\)		 real
  • length: 2
  • mass: 1
  • time: -2
 potential energy at the Earth's surface
  • str_note
4
5579 variable E_1
\(E_1\)		 real
  • length: 2
  • mass: 1
  • time: -2
 energy 1
  • str_note
9
6277 constant G
\(G\)		 real
  • length: 3
  • mass: -1
  • time: -2
 gravitational constant 6.67430*10^{-11}   m^3 * kg^-1 * s^-2
 60
8849 variable PE_2
\(PE_2\)		 real
  • length: 2
  • mass: 1
  • time: -2
 potential energy 11
4550 variable E_2
\(E_2\)		 real
  • length: 2
  • mass: 1
  • time: -2
 energy 2
  • str_note
9
1552 variable j
\(j\)		 ['integer'] dimensionless index 7
9398 variable dW
\(dW\)		 real
  • length: 2
  • mass: 1
  • time: -2
 differential work
  • str_note
2
1955 variable KE_1
\(KE_1\)		 real
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy 17
4851 variable m_2
\(m_2\)		 real
  • mass: 1
 mass 31
8656 variable v_{\rm escape}
\(v_{\rm escape}\)		 real
  • length: 1
  • time: -1
 escape velocity 12
1357 variable v
\(v\)		 ['real']
  • length: 1
  • time: -1
 velocity 83
2530 variable r
\(r\)		 ['real']
  • length: 1
 radius 60
4093 variable PE_1
\(PE_1\)		 real
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy 12
1352 variable KE_2
\(KE_2\)		 real
  • length: 2
  • mass: 1
  • time: -2
 kinetic energy 14
9199 variable dx
\(dx\)		 ['real']
  • length: 1
 15
5156 variable m
\(m\)		 ['real']
  • mass: 1
 mass 69
MESSAGES: