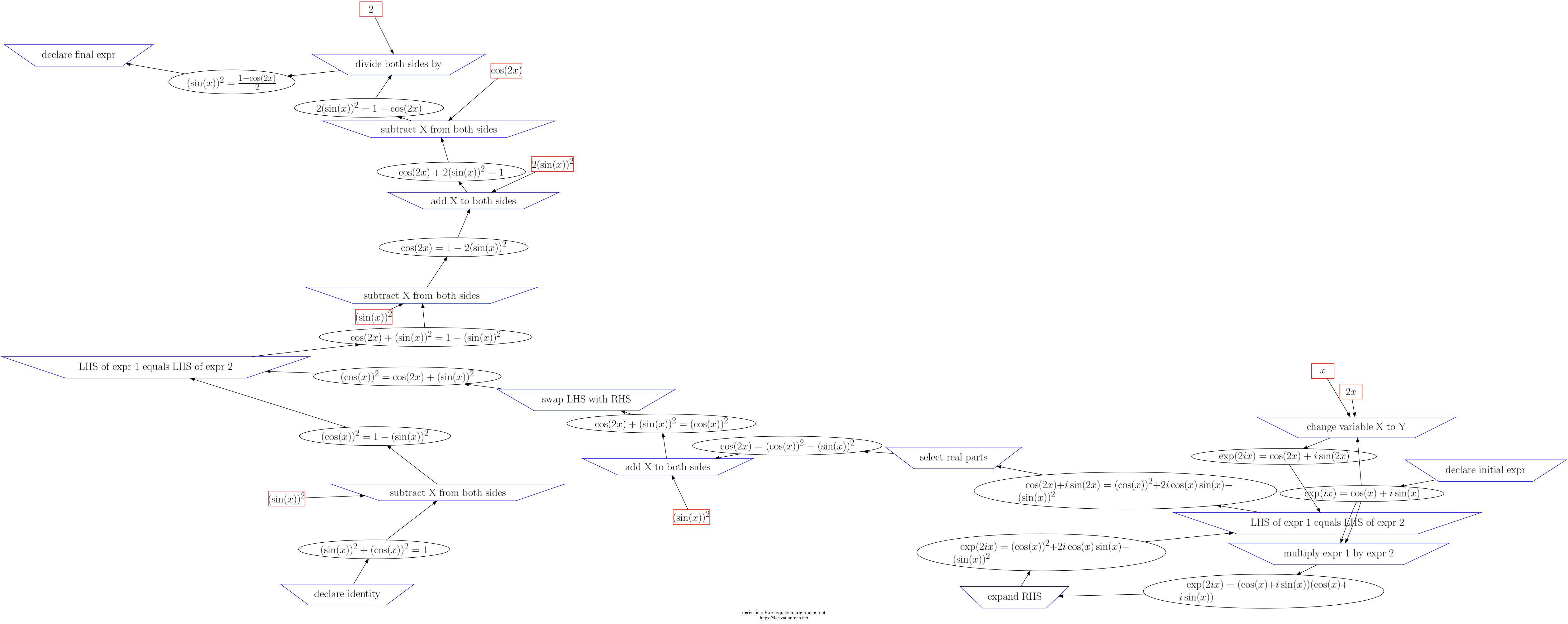
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 16 | declare final expr |
|
|
|
no validation is available for declarations |
9988949211:
|
9988949211:
|
|
| 8 | declare identity |
|
|
|
no validation is available for declarations |
5832984291:
error for dim with 5832984291 |
5832984291:
N/A |
|
| 15 | divide both sides by |
|
|
|
valid |
9889984281:
9988949211: |
9889984281:
9988949211: |
|
| 10 | swap LHS with RHS |
|
|
|
valid |
9482928243:
9482438243: |
9482928243:
9482438243: |
|
| 5 | expand RHS |
|
|
|
LHS diff is 0 RHS diff is (pdg4621**2 + 1)*sin(pdg1464)**2 |
4638429483:
4598294821: |
4638429483:
4598294821: |
|
| 2 | change variable X to Y |
|
|
|
LHS diff is (1 - exp(pdg1464*pdg4621))*exp(pdg1464*pdg4621) RHS diff is pdg4621*sin(pdg1464) - pdg4621*sin(2*pdg1464) + cos(pdg1464) - cos(2*pdg1464) |
4938429483:
4838429483: |
4938429483:
4838429483: |
|
| 12 | subtract X from both sides |
|
|
|
valid |
4827492911:
1248277773: |
4827492911:
1248277773: |
|
| 14 | subtract X from both sides |
|
|
|
valid |
7572664728:
9889984281: |
7572664728:
9889984281: |
|
| 13 | add X to both sides |
|
|
|
valid |
1248277773:
7572664728: |
1248277773:
7572664728: |
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
4938429483:
|
4938429483:
|
|
| 6 | select real parts |
|
|
|
LHS diff is -cos(2*pdg1464) + cos(2*re(pdg1464))*cosh(2*im(pdg1464)) + re(pdg4621*sin(2*pdg1464)) RHS diff is -cos(2*pdg1464) + 2*cos(2*re(pdg1464))*sinh(im(pdg1464))**2 + cos(2*re(pdg1464)) + re(pdg4621*sin(2*pdg1464)) |
9483928192:
9482928242: |
9483928192:
9482928242: |
|
| 7 | add X to both sides |
|
|
|
valid |
9482928242:
9482928243: |
9482928242:
9482928243: |
|
| 4 | multiply expr 1 by expr 2 |
|
|
|
valid |
4938429483:
4938429483: 4638429483: |
4938429483:
4938429483: 4638429483: |
|
| 11 | LHS of expr 1 equals LHS of expr 2 |
|
|
|
valid |
9482438243:
3285732911: error for dim with 3285732911 4827492911: |
9482438243:
3285732911: N/A 4827492911: |
|
| 3 | LHS of expr 1 equals LHS of expr 2 |
|
|
|
valid |
4598294821:
4838429483: 9483928192: |
4598294821:
4838429483: 9483928192: |
|
| 9 | subtract X from both sides |
|
|
|
valid |
5832984291:
error for dim with 5832984291 3285732911: error for dim with 3285732911 |
5832984291:
N/A 3285732911: N/A |