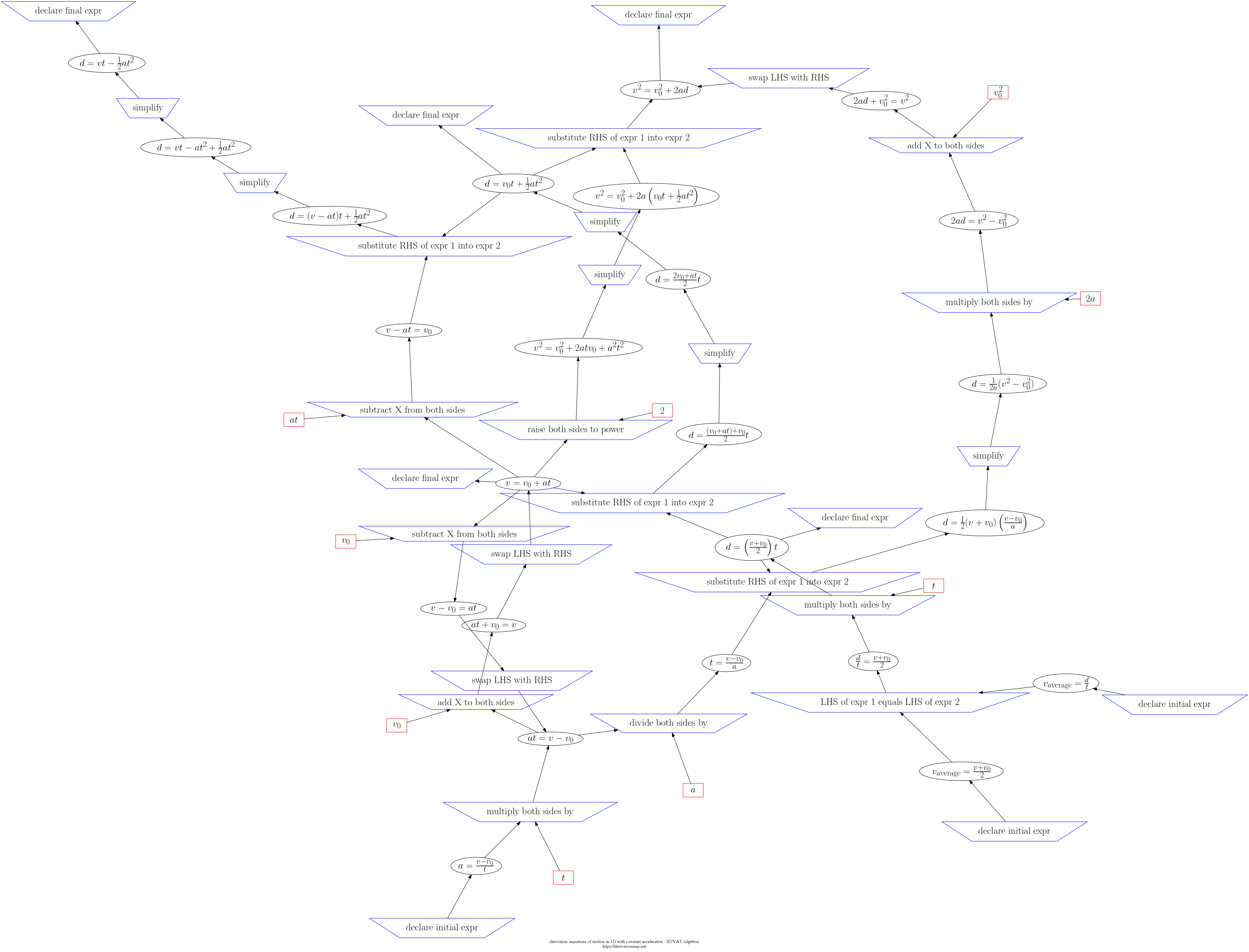
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
https://en.wikipedia.org/wiki/Equations_of_motion
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 19 | swap LHS with RHS |
|
|
|
valid |
9759901995:
4748157455: |
9759901995:
4748157455: |
|
| 30 | simplify |
|
|
|
valid |
4580545876:
6421241247: |
4580545876:
6421241247: |
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
3366703541:
|
3366703541:
|
|
| 3 | add X to both sides |
|
|
|
valid |
4748157455:
4798787814: |
4748157455:
4798787814: |
|
| 5 | declare final expr |
|
|
|
no validation is available for declarations |
3462972452:
|
3462972452:
|
|
| 14 | raise both sides to power |
|
|
|
no check is performed |
3462972452:
7215099603: |
3462972452:
7215099603: |
|
| 20 | divide both sides by |
|
|
|
valid |
4748157455:
1967582749: |
4748157455:
1967582749: |
|
| 12 | simplify |
|
|
|
valid |
1265150401:
9658195023: |
1265150401:
9658195023: |
|
| 31 | declare final expr |
|
|
|
no validation is available for declarations |
6421241247:
|
6421241247:
|
|
| 21 | substitute RHS of expr 1 into expr 2 |
|
|
|
LHS diff is 0 RHS diff is (pdg1357 + pdg5153)*(-pdg1357 + pdg1467*pdg9140 + pdg5153)/(2*pdg9140) |
1967582749:
8706092970: 5733721198: |
1967582749:
8706092970: 5733721198: |
|
| 13 | declare final expr |
|
|
|
no validation is available for declarations |
9658195023:
|
9658195023:
|
|
| 24 | add X to both sides |
|
|
|
valid |
8269198922:
4948763856: |
8269198922:
4948763856: |
|
| 16 | substitute RHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
5144263777:
9658195023: 7939765107: |
5144263777:
9658195023: 7939765107: |
|
| 9 | multiply both sides by |
|
|
|
valid |
9897284307:
8706092970: |
9897284307:
8706092970: |
|
| 17 | declare final expr |
|
|
|
no validation is available for declarations |
7939765107:
|
7939765107:
|
|
| 28 | substitute RHS of expr 1 into expr 2 |
|
|
|
valid |
6457044853:
9658195023: 1259826355: |
6457044853:
9658195023: 1259826355: |
|
| 29 | simplify |
|
|
|
valid |
1259826355:
4580545876: |
1259826355:
4580545876: |
|
| 8 | LHS of expr 1 equals LHS of expr 2 |
|
|
|
valid |
3411994811:
dimensions are consistent 6175547907: 9897284307: |
3411994811:
N/A 6175547907: 9897284307: |
|
| 10 | substitute RHS of expr 1 into expr 2 |
|
|
|
LHS diff is 0 RHS diff is pdg1467*(pdg1357 - pdg1467*pdg9140 - pdg5153)/2 |
3462972452:
8706092970: 7011114072: |
3462972452:
8706092970: 7011114072: |
|
| 23 | multiply both sides by |
|
|
|
valid |
5611024898:
8269198922: |
5611024898:
8269198922: |
|
| 2 | multiply both sides by |
|
|
|
valid |
3366703541:
4748157455: |
3366703541:
4748157455: |
|
| 27 | subtract X from both sides |
|
|
|
valid |
3462972452:
6457044853: |
3462972452:
6457044853: |
|
| 22 | simplify |
|
|
|
valid |
5733721198:
5611024898: |
5733721198:
5611024898: |
difference of squares |
| 18 | subtract X from both sides |
|
|
|
valid |
3462972452:
9759901995: |
3462972452:
9759901995: |
|
| 4 | swap LHS with RHS |
|
|
|
valid |
4798787814:
3462972452: |
4798787814:
3462972452: |
|
| 25 | swap LHS with RHS |
|
|
|
valid |
4948763856:
7939765107: |
4948763856:
7939765107: |
|
| 15 | simplify |
|
|
|
Nothing to split |
7215099603:
5144263777: |
7215099603:
5144263777: |
factored 2a out of two terms |
| 26 | declare final expr |
|
|
|
no validation is available for declarations |
8706092970:
|
8706092970:
|
|
| 11 | simplify |
|
|
|
valid |
7011114072:
1265150401: |
7011114072:
1265150401: |
|
| 7 | declare initial expr |
|
|
|
no validation is available for declarations |
6175547907:
|
6175547907:
|
|
| 6 | declare initial expr |
|
|
|
no validation is available for declarations |
3411994811:
dimensions are consistent |
3411994811:
N/A |