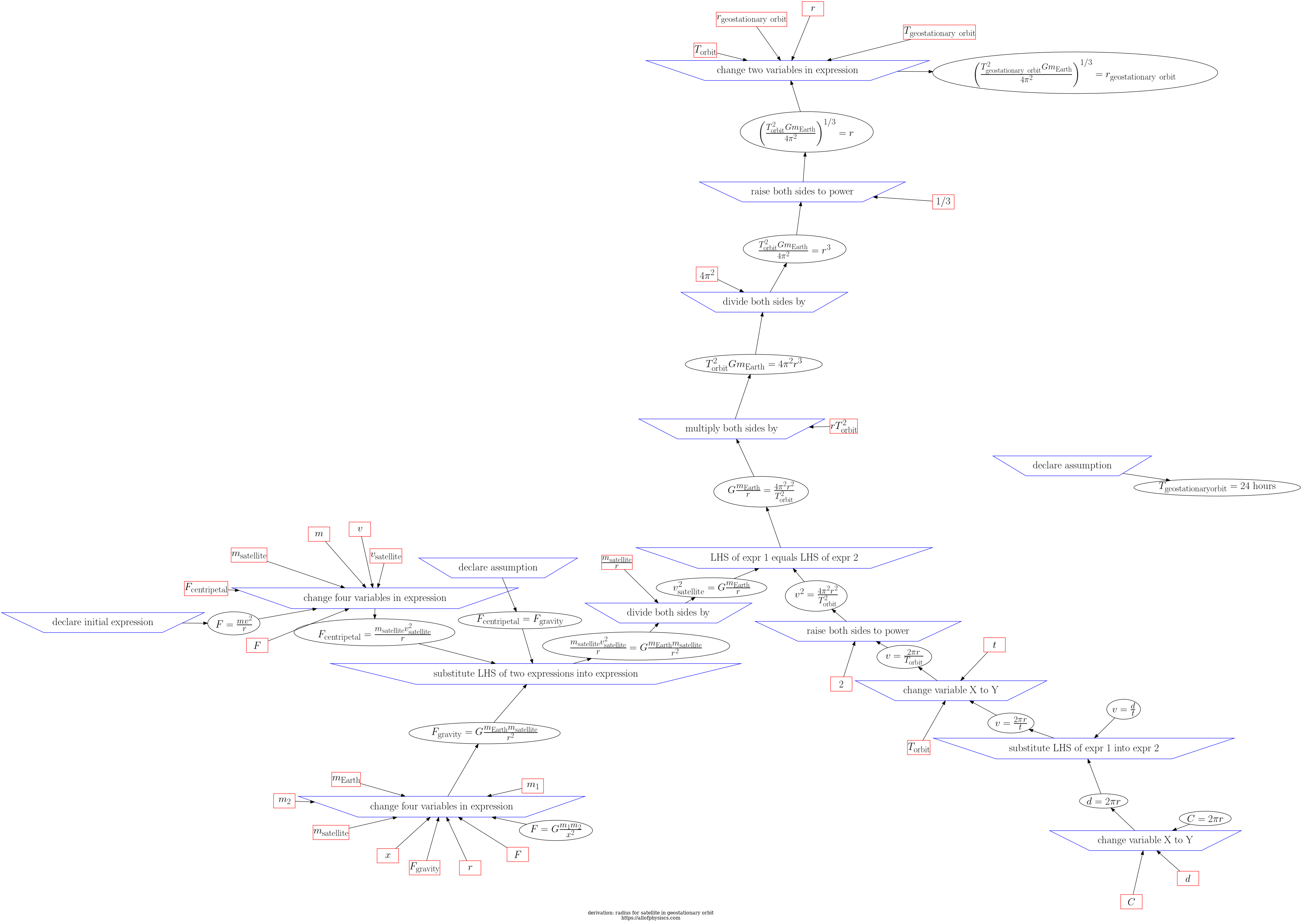
Return to navigation page or list derivations
| step | inference rule | input | feed | output | step validity (as per SymPy) |
|---|---|---|---|---|---|
| 1 |
|
|
|
|
LHS diff is -pdg0002867 + pdg0004037 RHS diff is pdg0003569*pdg0005022*pdg0006277/pdg0004037**2 - pdg0003569*pdg0005458*pdg0006277/pdg0002530**2 |
| 2 |
|
|
no validation is available for declarations | ||
| 3 |
|
|
|
|
list index out of range |
| 4 |
|
|
no validation is available for declarations | ||
| 5 |
|
|
|
recognized infrule but not yet supported | |
| 6 |
|
|
|
|
valid |
| 7 |
|
|
|
valid | |
| 8 |
|
|
|
|
LHS diff is 0 RHS diff is 2*pdg0002530*pdg0003141*(-pdg0001467 + pdg0008762)/(pdg0001467*pdg0008762) |
| 9 |
|
|
|
|
recognized infrule but not yet supported |
| 10 |
|
|
|
|
valid |
| 11 |
|
|
|
input diff is pdg0001357**2 - pdg0004082**2 diff is 4*pdg0002530**2*pdg0003141**2/pdg0008762**2 - pdg0005458*pdg0006277/pdg0002530 diff is -4*pdg0002530**2*pdg0003141**2/pdg0008762**2 + pdg0005458*pdg0006277/pdg0002530 | |
| 12 |
|
|
|
|
valid |
| 13 |
|
|
|
|
valid |
| 14 |
|
|
|
|
recognized infrule but not yet supported |
| 15 |
|
|
no validation is available for declarations | ||
| 16 |
|
|
|
|
list index out of range |
pdg_app/to_review_derivation: node_properties, derivation 2912081compute/get_dict_of_steps_in_derivation: steps_in_this_derivation5547629compute/get_dict_of_steps_in_derivation: step_has_inference_rule5876136compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5876136compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5876136compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5876136compute/get_dict_of_steps_in_derivation: get_step_has_sequence_index5547629compute/get_dict_of_steps_in_derivation: step_has_inference_rule2104854compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2104854compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2104854compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2104854compute/get_dict_of_steps_in_derivation: step_has_inference_rule8238485compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8238485compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8238485compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8238485compute/get_dict_of_steps_in_derivation: step_has_inference_rule6513955compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6513955compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6513955compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6513955compute/get_dict_of_steps_in_derivation: step_has_inference_rule4174561compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4174561compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4174561compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4174561compute/get_dict_of_steps_in_derivation: step_has_inference_rule8562599compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8562599compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8562599compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8562599compute/get_dict_of_steps_in_derivation: step_has_inference_rule3873446compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3873446compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3873446compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3873446compute/get_dict_of_steps_in_derivation: step_has_inference_rule5998393compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5998393compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5998393compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5998393compute/get_dict_of_steps_in_derivation: step_has_inference_rule7022154compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7022154compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7022154compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7022154compute/get_dict_of_steps_in_derivation: step_has_inference_rule3417942compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3417942compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3417942compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3417942compute/get_dict_of_steps_in_derivation: step_has_inference_rule6265175compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6265175compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6265175compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6265175compute/get_dict_of_steps_in_derivation: step_has_inference_rule2333251compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2333251compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2333251compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2333251compute/get_dict_of_steps_in_derivation: step_has_inference_rule5451071compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5451071compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5451071compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5451071compute/get_dict_of_steps_in_derivation: step_has_inference_rule4863287compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4863287compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4863287compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4863287compute/get_dict_of_steps_in_derivation: step_has_inference_rule3824673compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3824673compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3824673compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3824673compute/get_dict_of_steps_in_derivation: step_has_inference_rule5221060compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5221060compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5221060compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5221060pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation2912081pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id2912081282755pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule2912081compute/get_dict_of_steps_in_derivation: step_has_inference_rule4595273compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4595273compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4595273compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4595273compute/get_dict_of_steps_in_derivation: step_has_inference_rule7293690compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7293690compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7293690compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7293690compute/get_dict_of_steps_in_derivation: step_has_inference_rule3548848compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3548848compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3548848compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3548848compute/get_dict_of_steps_in_derivation: step_has_inference_rule5638171compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5638171compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5638171compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5638171compute/get_dict_of_steps_in_derivation: step_has_inference_rule9061311compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9061311compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9061311compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9061311compute/get_dict_of_steps_in_derivation: step_has_inference_rule8309733compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8309733compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8309733compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8309733compute/get_dict_of_steps_in_derivation: step_has_inference_rule4625574compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4625574compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4625574compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4625574compute/get_dict_of_steps_in_derivation: step_has_inference_rule7421244compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7421244compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7421244compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7421244compute/get_dict_of_steps_in_derivation: step_has_inference_rule6500899compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6500899compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6500899compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6500899compute/get_dict_of_steps_in_derivation: step_has_inference_rule5501835compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5501835compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5501835compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5501835compute/get_dict_of_steps_in_derivation: step_has_inference_rule9644843compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9644843compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9644843compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9644843compute/get_dict_of_steps_in_derivation: step_has_inference_rule7587286compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7587286compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7587286compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7587286compute/get_dict_of_steps_in_derivation: step_has_inference_rule9839967compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9839967compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9839967compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9839967compute/get_dict_of_steps_in_derivation: step_has_inference_rule6502548compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6502548compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6502548compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6502548compute/get_dict_of_steps_in_derivation: step_has_inference_rule1384194compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1384194compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1384194compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1384194compute/get_dict_of_steps_in_derivation: step_has_inference_rule4528089compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4528089compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4528089compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4528089compute/get_dict_of_steps_in_derivation: step_has_inference_rule2596505compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2596505compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2596505compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2596505compute/get_dict_of_steps_in_derivation: step_has_inference_rule9946751compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9946751compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9946751compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9946751compute/get_dict_of_steps_in_derivation: step_has_inference_rule3516876compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3516876compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3516876compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3516876compute/get_dict_of_steps_in_derivation: step_has_inference_rule8479990compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8479990compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8479990compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8479990compute/get_dict_of_steps_in_derivation: step_has_inference_rule6730420compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6730420compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6730420compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6730420compute/get_dict_of_steps_in_derivation: step_has_inference_rule9846171compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9846171compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9846171compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9846171compute/get_dict_of_steps_in_derivation: step_has_inference_rule2337738compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2337738compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2337738compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2337738compute/get_dict_of_steps_in_derivation: step_has_inference_rule5542498compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5542498compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5542498compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5542498compute/get_dict_of_steps_in_derivation: step_has_inference_rule1591438compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1591438compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1591438compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1591438compute/get_dict_of_steps_in_derivation: step_has_inference_rule3570472compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3570472compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3570472compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3570472compute/get_dict_of_steps_in_derivation: step_has_inference_rule7724473compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7724473compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7724473compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7724473compute/get_dict_of_steps_in_derivation: step_has_inference_rule2160629compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2160629compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2160629compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2160629compute/get_dict_of_steps_in_derivation: step_has_inference_rule4631971compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4631971compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4631971compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4631971compute/get_dict_of_steps_in_derivation: step_has_inference_rule4261533compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4261533compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4261533compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4261533compute/get_dict_of_steps_in_derivation: step_has_inference_rule8412924compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8412924compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8412924compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8412924compute/get_dict_of_steps_in_derivation: step_has_inference_rule9981266compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9981266compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9981266compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9981266