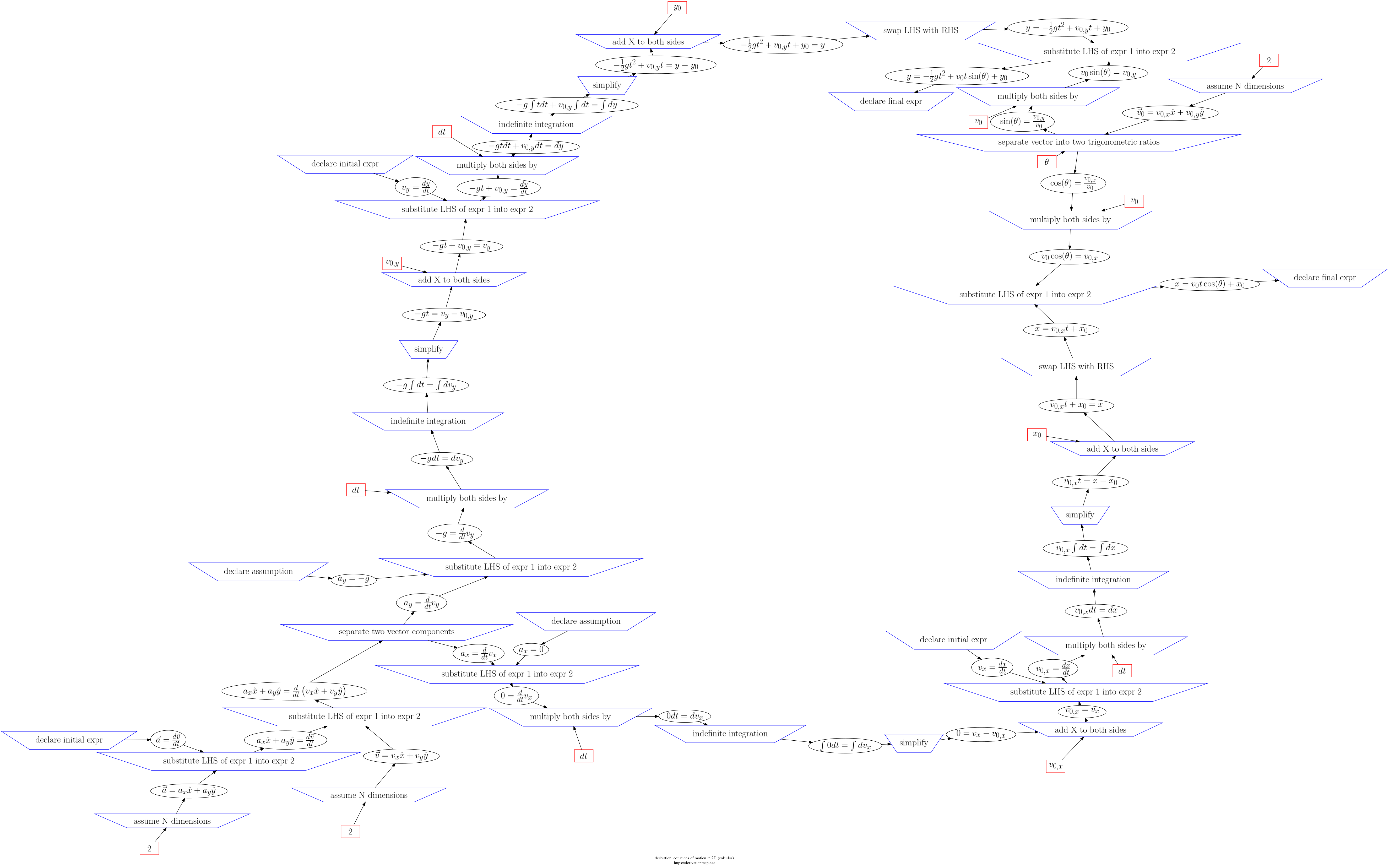
This page contains three views of the steps in the derivation: d3js, graphviz PNG, and a table.
Notes for this derivation:
| Index | Inference Rule | Input latex | Feeds latex | Output latex | step validity | dimension check | unit check | notes |
|---|---|---|---|---|---|---|---|---|
| 28 | substitute LHS of expr 1 into expr 2 |
|
|
|
LHS diff is -pdg2958 + pdg5505 RHS diff is 0 |
6134836751:
dimensions are consistent 8460820419: 7455581657: |
6134836751:
N/A 8460820419: 7455581657: |
|
| 17 | declare initial expr |
|
|
|
no validation is available for declarations |
7252338326:
|
7252338326:
|
|
| 23 | multiply both sides by |
|
|
|
LHS diff is 0 RHS diff is -pdg5005 |
8750379055:
1166310428: |
8750379055:
1166310428: |
|
| 10 | assume N dimensions |
|
|
|
no validation is available for assumptions |
5349866551:
|
5349866551:
|
|
| 29 | multiply both sides by |
|
|
|
LHS diff is 0 RHS diff is -pdg9199 |
7455581657:
1963253044: |
7455581657:
1963253044: |
|
| 16 | add X to both sides |
|
|
|
LHS diff is 0 RHS diff is -pdg5153 - pdg9107 + 2*pdg9431 |
9973952056:
6572039835: |
9973952056:
6572039835: |
|
| 11 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
9707028061:
1819663717: 8750379055: |
9707028061:
1819663717: 8750379055: |
|
| 30 | indefinite integration |
|
|
|
no check performed |
1963253044:
3676159007: |
1963253044:
3676159007: |
|
| 39 | multiply both sides by |
|
|
|
LHS diff is 0 RHS diff is pdg5153**2/pdg9431 - pdg9431 |
7376526845:
8949329361: |
7376526845:
8949329361: |
|
| 33 | swap LHS with RHS |
|
|
|
valid |
8486706976:
1306360899: |
8486706976:
1306360899: |
|
| 12 | substitute LHS of expr 1 into expr 2 |
|
|
|
valid |
2741489181:
8228733125: 1977955751: |
2741489181:
8228733125: 1977955751: |
|
| 6 | separate two vector components |
|
|
|
no check performed |
7729413831:
1819663717: 8228733125: |
7729413831:
1819663717: 8228733125: |
|
| 13 | multiply both sides by |
|
|
|
LHS diff is pdg1649*(dt - pdg4711) RHS diff is -pdg5674 |
1977955751:
1702349646: |
1977955751:
1702349646: |
|
| 37 | substitute LHS of expr 1 into expr 2 |
|
|
|
LHS diff is 0 RHS diff is pdg1467*(pdg2958 - pdg5153*cos(pdg1575)) |
6083821265:
1306360899: 5438722682: |
6083821265:
1306360899: 5438722682: |
|
| 14 | indefinite integration |
|
|
|
no check performed |
1702349646:
8584698994: |
1702349646:
8584698994: |
|
| 40 | swap LHS with RHS |
|
|
|
LHS diff is pdg1467*(-pdg9107 + pdg9431) RHS diff is pdg1467*(-pdg9107 + pdg9431) |
2461349007:
1405465835: |
2461349007:
1405465835: |
|
| 22 | add X to both sides |
|
|
|
valid |
2858549874:
2461349007: |
2858549874:
2461349007: |
|
| 15 | simplify |
|
|
|
LHS diff is -dt*g + pdg1467*pdg1649 RHS diff is pdg5153 + pdg5674 - pdg9431 |
8584698994:
9973952056: |
8584698994:
9973952056: |
|
| 7 | declare assumption |
|
|
|
no validation is available for declarations |
9707028061:
|
9707028061:
|
define the orientation of the coordinate system with respect to the gravitational acceleration such that x axis is perpendicular to gravity |
| 8 | declare assumption |
|
|
|
no validation is available for declarations |
2741489181:
|
2741489181:
|
define the orientation of the coordinate system with respect to the gravitational acceleration such that y axis is parallel to gravity |
| 36 | multiply both sides by |
|
|
|
LHS diff is 0 RHS diff is -pdg2958 + pdg5153**2/pdg2958 |
7391837535:
6083821265: |
7391837535:
6083821265: |
|
| 32 | add X to both sides |
|
|
|
valid |
9882526611:
8486706976: |
9882526611:
8486706976: |
|
| 5 | substitute LHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
5349866551:
4158986868: 7729413831: |
5349866551:
4158986868: 7729413831: |
|
| 24 | indefinite integration |
|
|
|
no check performed |
1166310428:
2366691988: |
1166310428:
2366691988: |
|
| 42 | declare final expr |
|
|
|
no validation is available for declarations |
9862900242:
|
9862900242:
|
|
| 38 | declare final expr |
|
|
|
no validation is available for declarations |
5438722682:
|
5438722682:
|
|
| 9 | assume N dimensions |
|
|
|
no validation is available for assumptions |
8602512487:
|
8602512487:
|
|
| 18 | substitute LHS of expr 1 into expr 2 |
|
|
|
LHS diff is pdg1467*(-pdg1649 + pdg6277) RHS diff is 0 |
7252338326:
6572039835: 6204539227: |
7252338326:
6572039835: 6204539227: |
|
| 27 | declare initial expr |
|
|
|
no validation is available for declarations |
8460820419:
|
8460820419:
|
|
| 25 | simplify |
|
|
|
LHS diff is 0 RHS diff is pdg2958 + pdg5005 - pdg5505 |
2366691988:
1676472948: error for dim with 1676472948 |
2366691988:
1676472948: N/A |
|
| 3 | substitute LHS of expr 1 into expr 2 |
|
|
|
Nothing to split |
3169580383:
8602512487: 4158986868: |
3169580383:
8602512487: 4158986868: |
|
| 20 | indefinite integration |
|
|
|
no check performed |
8145337879:
8808860551: |
8145337879:
8808860551: |
|
| 35 | separate vector into two trigonometric ratios |
|
|
|
no check performed |
9341391925:
7391837535: 7376526845: |
9341391925:
7391837535: 7376526845: |
|
| 41 | substitute LHS of expr 1 into expr 2 |
|
|
|
LHS diff is 0 RHS diff is pdg1467*(-pdg5153*sin(pdg1575) + pdg9107) |
8949329361:
1405465835: 9862900242: |
8949329361:
1405465835: 9862900242: |
|
| 21 | simplify |
|
|
|
LHS diff is 0 RHS diff is pdg1469 |
8808860551:
2858549874: |
8808860551:
2858549874: |
|
| 31 | simplify |
|
|
|
LHS diff is 0 RHS diff is pdg1464 + pdg1572 - pdg4037 |
3676159007:
9882526611: |
3676159007:
9882526611: |
|
| 34 | assume N dimensions |
|
|
|
no validation is available for assumptions |
9341391925:
|
9341391925:
|
|
| 19 | multiply both sides by |
|
|
|
LHS diff is pdg1467*pdg4711*(pdg1649 - pdg6277) RHS diff is -pdg5842 |
6204539227:
8145337879: |
6204539227:
8145337879: |
|
| 1 | declare initial expr |
|
|
|
no validation is available for declarations |
3169580383:
|
3169580383:
|
|
| 26 | add X to both sides |
|
|
|
valid |
1676472948:
error for dim with 1676472948 6134836751: dimensions are consistent |
1676472948:
N/A 6134836751: N/A |
| symbol ID | category | latex | scope | dimension | name | value | Used in derivations | references | |
|---|---|---|---|---|---|---|---|---|---|
| 4037 | variable |
x
\(x\) |
['real'] |
|
position |
|
53 | ||
| 1700 | variable |
\hat{y}
\(\hat{y}\) |
real | dimensionless | unit vector | 4 | |||
| 1469 | variable |
y_0
\(y_0\) |
['real'] |
|
initial position | 9 | |||
| 6277 | constant |
G
\(G\) |
real |
|
gravitational constant |
6.67430*10^{-11} m^3 * kg^-1 * s^-2 |
|
60 | |
| 1464 | variable |
x
\(x\) |
['real'] | dimensionless |
|
140 | |||
| 9431 | variable |
v_{0, y}
\(v_{0, y}\) |
['real'] |
|
initial velocity along y axis | 12 | |||
| 7055 | variable |
a_y
\(a_y\) |
real |
|
acceleration along y axis | 4 | |||
| 5842 | variable |
dy
\(dy\) |
['real'] |
|
differential displacement along y axis |
|
2 | ||
| 5647 | variable |
y
\(y\) |
['real'] |
|
position | 14 | |||
| 2958 | variable |
v_{0, x}
\(v_{0, x}\) |
['real'] |
|
initial velocity along x axis | 15 | |||
| 5153 | variable |
v_0
\(v_0\) |
['real'] |
|
initial velocity | 44 | |||
| 5505 | variable |
v_x
\(v_x\) |
real |
|
velocity along x axis |
|
7 | ||
| 1467 | variable |
t
\(t\) |
['real'] |
|
time |
|
121 | ||
| 1572 | variable |
x_0
\(x_0\) |
['real'] |
|
initial position | 11 | |||
| 7159 | variable |
a_x
\(a_x\) |
real |
|
acceleration along x axis | 4 | |||
| 9107 | variable |
v_y
\(v_y\) |
real |
|
velocity along y axis |
|
7 | ||
| 2423 | variable |
\vec{a}
\(\vec{a}\) |
real |
|
acceleration |
|
2 | ||
| 4711 | variable |
dt
\(dt\) |
['real'] |
|
differential time |
|
7 | ||
| 1575 | variable |
\theta
\(\theta\) |
['real'] | dimensionless | angle | 34 | |||
| 6091 | variable |
\vec{v}_0
\(\vec{v}_0\) |
['real'] |
|
initial velocity | 1 | |||
| 8339 | variable |
\hat{x}
\(\hat{x}\) |
real | dimensionless | unit vector | 4 | |||
| 5674 | variable |
d v_y
\(d v_y\) |
['real'] |
|
differential velocity along y axis | 2 | |||
| 1649 | variable |
g
\(g\) |
['real'] |
|
acceleration due to gravity | 27 | |||
| 5005 | variable |
d v_x
\(d v_x\) |
['real'] |
|
differential velocity along x axis | 2 | |||
| 9199 | variable |
dx
\(dx\) |
['real'] |
|
15 | ||||
| 6373 | variable |
\vec{v}
\(\vec{v}\) |
real |
|
velocity |
|
2 |