Welcome to the Physics Derivation Graph

MESSAGES:

pdg_app/to_review_derivation sympy_validate_step.validate_step: TypeErrorType Tuple cannot be instantiated; use tuple() instead
pdg_app/to_review_derivation sympy_validate_step.validate_step: TypeErrorType Tuple cannot be instantiated; use tuple() instead
pdg_app/to_review_derivation sympy_validate_step.validate_step: TypeErrorType Tuple cannot be instantiated; use tuple() instead
pdg_app/to_review_derivation sympy_validate_step.validate_step: SyntaxErrorinvalid syntax (<string>, line 0)

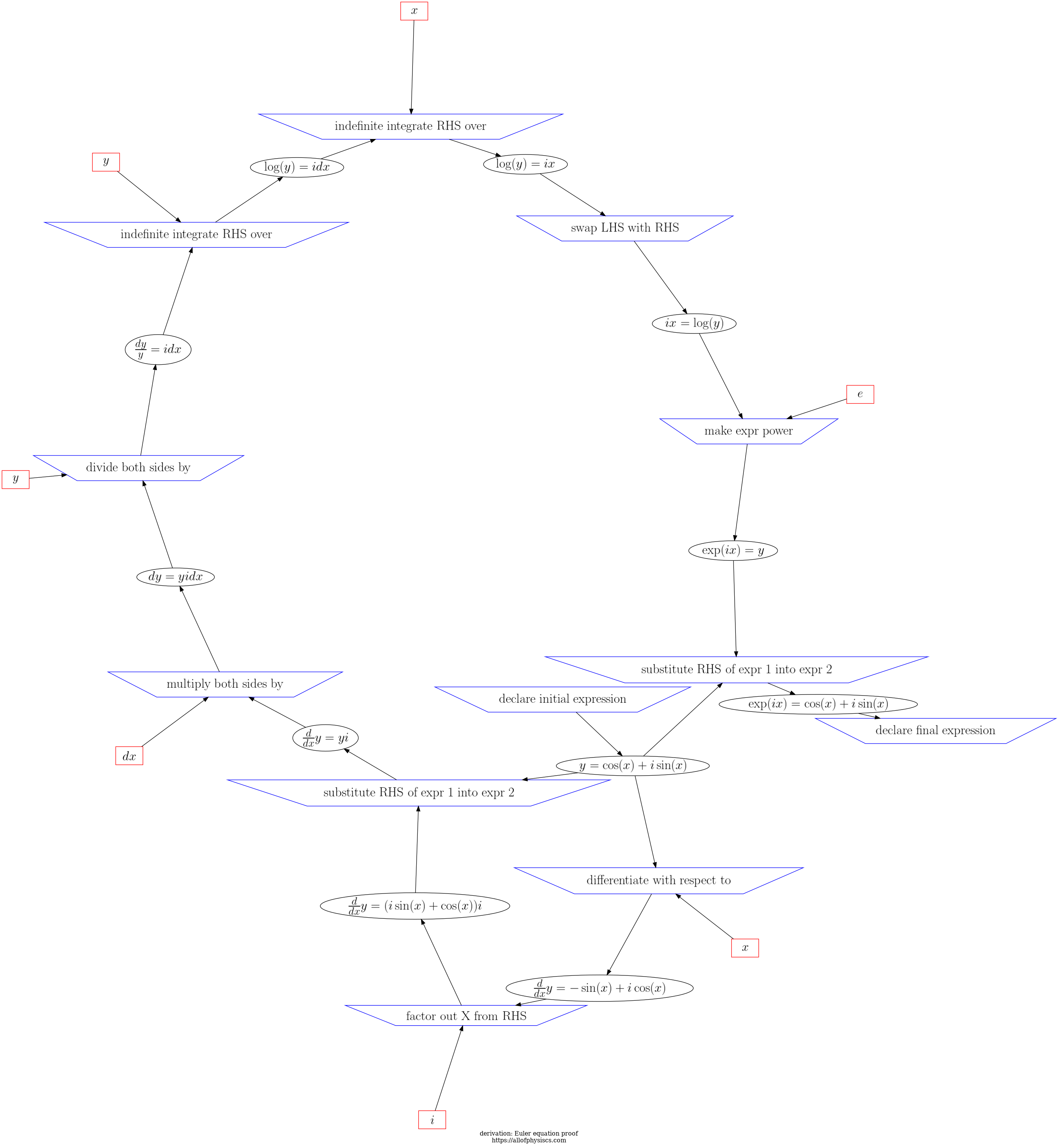
Return to navigation page or list derivations

Review Euler equation proof

abstract:
reference:

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			9492920340 $y=\cos(x)+i \sin(x)$	no validation is available for declarations
2	111649: differentiate with respect to number of inputs: 1; feeds: 1; outputs: 1 Differentiate Eq.~\\ref{eq:#2} with respect to $#1$; yields Eq.~\\ref{eq:#3}.	9492920340 $y=\cos(x)+i \sin(x)$	0007636749 $x$	9429829482 $\frac{d}{dx} y=-\sin(x) + i\cos(x)$	recognized infrule but not yet supported
3	111260: factor out X from RHS number of inputs: 1; feeds: 1; outputs: 1 Factor $#1$ from the RHS of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9429829482 $\frac{d}{dx} y=-\sin(x) + i\cos(x)$	0007563791 $i$	9482984922 $\frac{d}{dx} y=(i\sin(x) + \cos(x)) i$	Type Tuple cannot be instantiated; use tuple() instead
4	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9482984922 $\frac{d}{dx} y=(i\sin(x) + \cos(x)) i$ 9492920340 $y=\cos(x)+i \sin(x)$		9848294829 $\frac{d}{dx} y=y i$	Type Tuple cannot be instantiated; use tuple() instead
5	111182: multiply both sides by number of inputs: 1; feeds: 1; outputs: 1 Multiply both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	9848294829 $\frac{d}{dx} y=y i$	0003954314 $dx$	9848292229 $dy=y i dx$	Type Tuple cannot be instantiated; use tuple() instead
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	9848292229 $dy=y i dx$	0009877781 $y$	9482113948 $\frac{dy}{y}=i dx$	invalid syntax (<string>, line 0)
7	111132: indefinite integrate RHS over number of inputs: 1; feeds: 1; outputs: 1 Indefinite integral of RHS of Eq.~\\ref{eq:#2} over $#1$; yields Eq.~\\ref{eq:#3}.	9482113948 $\frac{dy}{y}=i dx$	0004264724 $y$	9482943948 $\log(y)=i dx$	recognized infrule but not yet supported
8	111132: indefinite integrate RHS over number of inputs: 1; feeds: 1; outputs: 1 Indefinite integral of RHS of Eq.~\\ref{eq:#2} over $#1$; yields Eq.~\\ref{eq:#3}.	9482943948 $\log(y)=i dx$	0006563727 $x$	4928239482 $\log(y)=i x$	recognized infrule but not yet supported
9	111268: swap LHS with RHS number of inputs: 1; feeds: 0; outputs: 1 Swap LHS of Eq.~\\ref{eq:#1} with RHS; yields Eq.~\\ref{eq:#2}.	4928239482 $\log(y)=i x$		4923339482 $i x=\log(y)$	valid
10	111721: make expr power number of inputs: 1; feeds: 1; outputs: 1 Make Eq.~\\ref{eq:#2} the power of $#1$; yields Eq.~\\ref{eq:#3}.	4923339482 $i x=\log(y)$	0006656532 $e$	9482923849 $\exp(i x)=y$	LHS diff is -pdg0002718*(pdg0001464pdg0004621) + exp(pdg0001464pdg0004621) RHS diff is pdg0001452 - pdg0002718*(log(pdg0001452)/log(10))
11	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9492920340 $y=\cos(x)+i \sin(x)$ 9482923849 $\exp(i x)=y$		4938429483 $\exp(i x)=\cos(x)+i \sin(x)$	LHS diff is 0 RHS diff is pdg0001452 - pdg0004621*sin(pdg0001464) - cos(pdg0001464)
12	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	4938429483 $\exp(i x)=\cos(x)+i \sin(x)$			no validation is available for declarations

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.013 seconds for pdg_app/to_review_derivation: node_properties, derivation 6820096
0.004 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation1118202
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8180801
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8180801
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8180801
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8180801
0.004 seconds for compute/get_dict_of_steps_in_derivation: get_step_has_sequence_index1118202
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8266640
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8266640
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8266640
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8266640
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4090158
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4090158
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4090158
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4090158
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8478688
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8478688
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8478688
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8478688
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2025528
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2025528
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2025528
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2025528
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3535202
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3535202
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3535202
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3535202
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6713302
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6713302
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6713302
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6713302
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9847183
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9847183
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9847183
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9847183
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2456295
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2456295
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2456295
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2456295
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6353093
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6353093
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6353093
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6353093
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6528313
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6528313
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6528313
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6528313
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6742579
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6742579
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6742579
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6742579
0.003 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation6820096
0.006 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id6820096000001
0.019 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule6820096
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6675679
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6675679
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6675679
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6675679
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4621208
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4621208
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4621208
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4621208
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9738862
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9738862
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9738862
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9738862
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5158793
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5158793
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5158793
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5158793
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3031213
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3031213
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3031213
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3031213
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2719620
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2719620
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2719620
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2719620
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5580940
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5580940
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5580940
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5580940
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7424745
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7424745
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7424745
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7424745
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6341434
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6341434
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6341434
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6341434
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7250079
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7250079
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7250079
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7250079
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9112590
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9112590
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9112590
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9112590
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5545346
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5545346
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5545346
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5545346
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3225217
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3225217
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3225217
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3225217
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2920908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2920908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2920908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2920908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1572604
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1572604
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1572604
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1572604
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6651364
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6651364
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6651364
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6651364
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9847643
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9847643
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9847643
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9847643
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6251388
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6251388
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6251388
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6251388
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4459150
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4459150
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4459150
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4459150
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1179655
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1179655
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1179655
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1179655
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5304354
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5304354
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5304354
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5304354
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2044117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2044117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2044117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2044117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7047339
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7047339
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7047339
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7047339
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9389458
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9389458
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9389458
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9389458

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			9492920340 \(y=\cos(x)+i \sin(x)\)	no validation is available for declarations
2	111649: differentiate with respect to number of inputs: 1; feeds: 1; outputs: 1 Differentiate Eq.~\\ref{eq:#2} with respect to $#1$; yields Eq.~\\ref{eq:#3}.	9492920340 \(y=\cos(x)+i \sin(x)\)	0007636749 \(x\)	9429829482 \(\frac{d}{dx} y=-\sin(x) + i\cos(x)\)	recognized infrule but not yet supported
3	111260: factor out X from RHS number of inputs: 1; feeds: 1; outputs: 1 Factor $#1$ from the RHS of Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9429829482 \(\frac{d}{dx} y=-\sin(x) + i\cos(x)\)	0007563791 \(i\)	9482984922 \(\frac{d}{dx} y=(i\sin(x) + \cos(x)) i\)	Type Tuple cannot be instantiated; use tuple() instead
4	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9482984922 \(\frac{d}{dx} y=(i\sin(x) + \cos(x)) i\) 9492920340 \(y=\cos(x)+i \sin(x)\)		9848294829 \(\frac{d}{dx} y=y i\)	Type Tuple cannot be instantiated; use tuple() instead
5	111182: multiply both sides by number of inputs: 1; feeds: 1; outputs: 1 Multiply both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	9848294829 \(\frac{d}{dx} y=y i\)	0003954314 \(dx\)	9848292229 \(dy=y i dx\)	Type Tuple cannot be instantiated; use tuple() instead
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	9848292229 \(dy=y i dx\)	0009877781 \(y\)	9482113948 \(\frac{dy}{y}=i dx\)	invalid syntax (<string>, line 0)
7	111132: indefinite integrate RHS over number of inputs: 1; feeds: 1; outputs: 1 Indefinite integral of RHS of Eq.~\\ref{eq:#2} over $#1$; yields Eq.~\\ref{eq:#3}.	9482113948 \(\frac{dy}{y}=i dx\)	0004264724 \(y\)	9482943948 \(\log(y)=i dx\)	recognized infrule but not yet supported
8	111132: indefinite integrate RHS over number of inputs: 1; feeds: 1; outputs: 1 Indefinite integral of RHS of Eq.~\\ref{eq:#2} over $#1$; yields Eq.~\\ref{eq:#3}.	9482943948 \(\log(y)=i dx\)	0006563727 \(x\)	4928239482 \(\log(y)=i x\)	recognized infrule but not yet supported
9	111268: swap LHS with RHS number of inputs: 1; feeds: 0; outputs: 1 Swap LHS of Eq.~\\ref{eq:#1} with RHS; yields Eq.~\\ref{eq:#2}.	4928239482 \(\log(y)=i x\)		4923339482 \(i x=\log(y)\)	valid
10	111721: make expr power number of inputs: 1; feeds: 1; outputs: 1 Make Eq.~\\ref{eq:#2} the power of $#1$; yields Eq.~\\ref{eq:#3}.	4923339482 \(i x=\log(y)\)	0006656532 \(e\)	9482923849 \(\exp(i x)=y\)	LHS diff is -pdg0002718*(pdg0001464pdg0004621) + exp(pdg0001464pdg0004621) RHS diff is pdg0001452 - pdg0002718*(log(pdg0001452)/log(10))
11	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9492920340 \(y=\cos(x)+i \sin(x)\) 9482923849 \(\exp(i x)=y\)		4938429483 \(\exp(i x)=\cos(x)+i \sin(x)\)	LHS diff is 0 RHS diff is pdg0001452 - pdg0004621*sin(pdg0001464) - cos(pdg0001464)
12	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	4938429483 \(\exp(i x)=\cos(x)+i \sin(x)\)			no validation is available for declarations