Welcome to the Physics Derivation Graph

Return to navigation page or list derivations

Review electric field wave equation: from time dependent to time independent

abstract:
reference:

step	inference rule	input	feed	output	validity (as per SymPy)
5	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	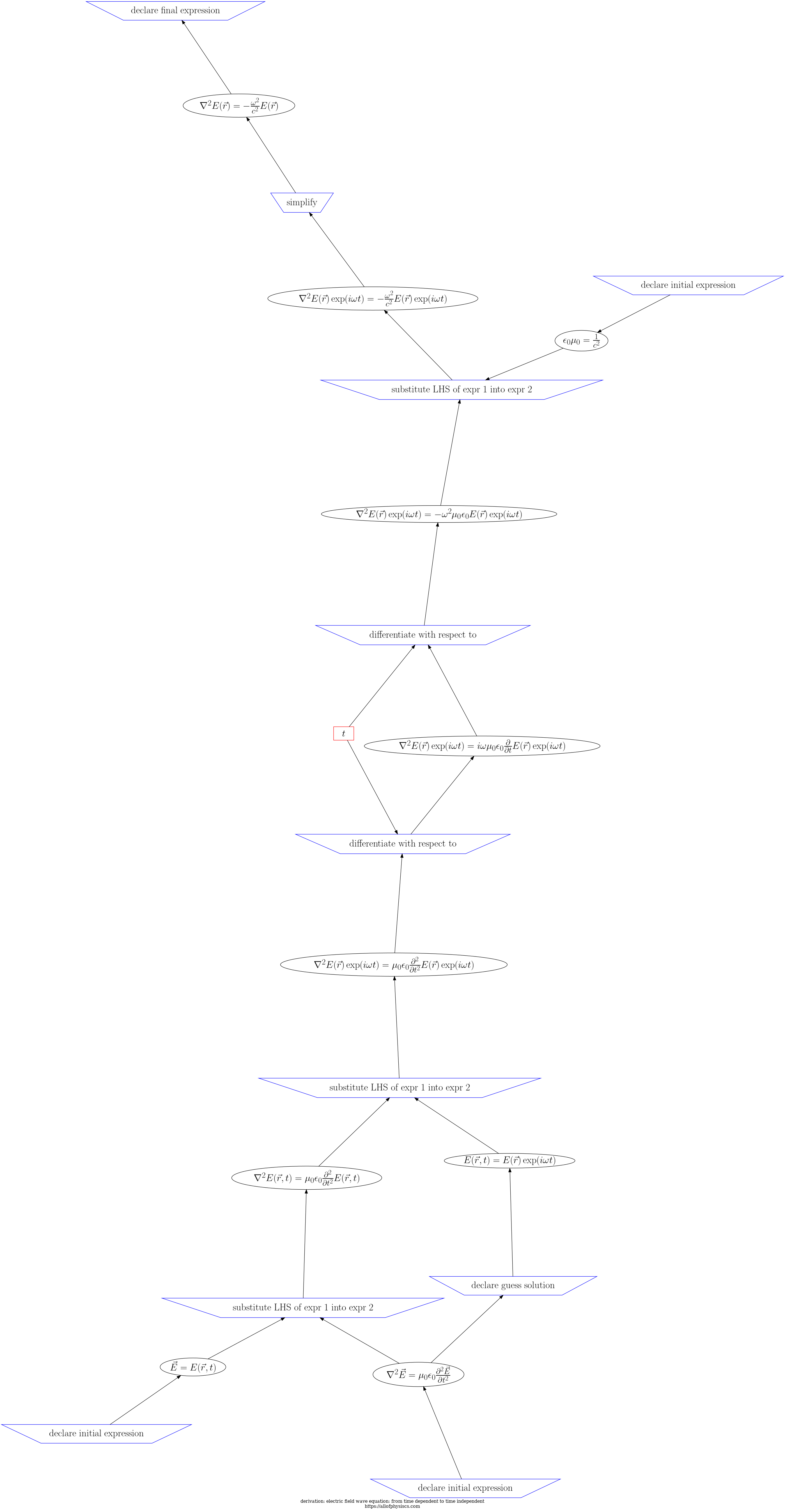9394939493 $\nabla^2 E( \vec{r},t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r},t)$ 9499428242 $E( \vec{r},t)=E( \vec{r})\exp(i \omega t)$		2029293929 $\nabla^2 E( \vec{r})\exp(i \omega t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r})\exp(i \omega t)$	LHS diff is -nabla*2pdg0006238(pdg0009472)exp(pdg0001467pdg0002321pdg0004621) + pdg0006238(pdg0009472, pdg0001467) RHS diff is (-partialpdg0006197pdg0007940exp(pdg0001467pdg0002321pdg0004621) + pdg0001467*2pdg0002718(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472)/pdg0001467*2
6	ID: 111649; differentiate with respect to number of inputs: 1; feeds: 1; outputs: 1 Differentiate Eq.~\\ref{eq:#2} with respect to $#1$; yields Eq.~\\ref{eq:#3}.	2029293929 $\nabla^2 E( \vec{r})\exp(i \omega t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r})\exp(i \omega t)$	0003232242 $t$	4985825552 $\nabla^2 E( \vec{r})\exp(i \omega t)=i \omega \mu_0 \epsilon_0 \frac{\partial}{\partial t} E( \vec{r})\exp(i \omega t)$	recognized infrule but not yet supported
2	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8572852424 $\vec{E}=E( \vec{r},t)$	no validation is available for declarations
3	ID: 111237; declare guess solution number of inputs: 1; feeds: 0; outputs: 1 Judicious choice as a guessed solution to Eq.~\\ref{eq:#1} is Eq.~\\ref{eq:#2},	8494839423 $\nabla^2 \vec{E}=\mu_0 \epsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}$		9499428242 $E( \vec{r},t)=E( \vec{r})\exp(i \omega t)$	no validation is available for declarations
4	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	8494839423 $\nabla^2 \vec{E}=\mu_0 \epsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}$ 8572852424 $\vec{E}=E( \vec{r},t)$		9394939493 $\nabla^2 E( \vec{r},t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r},t)$	LHS diff is -nabla*2pdg0006238(pdg0009472, pdg0001467) + pdg0004326 RHS diff is (-partialpdg0006197pdg0007940 + pdg0001467*2)pdg0006238(pdg0009472, pdg0001467)/pdg0001467**2
7	ID: 111649; differentiate with respect to number of inputs: 1; feeds: 1; outputs: 1 Differentiate Eq.~\\ref{eq:#2} with respect to $#1$; yields Eq.~\\ref{eq:#3}.	4985825552 $\nabla^2 E( \vec{r})\exp(i \omega t)=i \omega \mu_0 \epsilon_0 \frac{\partial}{\partial t} E( \vec{r})\exp(i \omega t)$	0003232242 $t$	1858578388 $\nabla^2 E( \vec{r})\exp(i \omega t)=- \omega^2 \mu_0 \epsilon_0 E( \vec{r})\exp(i \omega t)$	recognized infrule but not yet supported
10	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	9485384858 $\nabla^2 E( \vec{r})\exp(i \omega t)=- \frac{\omega^2}{c^2} E( \vec{r})\exp(i \omega t)$		3485475729 $\nabla^2 E( \vec{r})=- \frac{\omega^2}{c^2} E( \vec{r})$	LHS diff is nabla*2(pdg0002718(pdg0001467pdg0002321pdg0004621) - 1)pdg0006238(pdg0009472) RHS diff is pdg00023212(1 - pdg0002718(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472)/pdg0004567*2
11	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	3485475729 $\nabla^2 E( \vec{r})=- \frac{\omega^2}{c^2} E( \vec{r})$			no validation is available for declarations
9	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	4585828572 $\epsilon_0 \mu_0=\frac{1}{c^2}$ 1858578388 $\nabla^2 E( \vec{r})\exp(i \omega t)=- \omega^2 \mu_0 \epsilon_0 E( \vec{r})\exp(i \omega t)$		9485384858 $\nabla^2 E( \vec{r})\exp(i \omega t)=- \frac{\omega^2}{c^2} E( \vec{r})\exp(i \omega t)$	LHS diff is nabla*2(-pdg0002718(pdg0001467pdg0002321pdg0004621) + exp(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472) RHS diff is pdg00023212(pdg0002718(pdg0001467pdg0002321pdg0004621) - exp(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472)/pdg0004567*2
1	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8494839423 $\nabla^2 \vec{E}=\mu_0 \epsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}$	no validation is available for declarations
8	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			4585828572 $\epsilon_0 \mu_0=\frac{1}{c^2}$	no validation is available for declarations

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.008 seconds for pdg_app/to_review_derivation: node_properties, derivation2259912
0.011 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation1684541
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3893737
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3893737
0.016 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3893737
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3893737
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_sequence_index1684541
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3747009
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3747009
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3747009
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3747009
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8652464
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8652464
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8652464
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8652464
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5516417
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5516417
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5516417
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5516417
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8141704
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8141704
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8141704
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8141704
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1904552
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1904552
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1904552
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1904552
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9637542
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9637542
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9637542
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9637542
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3221728
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3221728
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3221728
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3221728
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4072190
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4072190
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4072190
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4072190
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1427077
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1427077
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1427077
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1427077
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5939030
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5939030
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5939030
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5939030
0.005 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation2259912
0.007 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id2259912000007
0.02 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule2259912
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8097560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8097560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8097560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8097560
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2136034
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2136034
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2136034
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2136034
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4719081
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4719081
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4719081
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4719081
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9665066
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9665066
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9665066
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9665066
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9699261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9699261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9699261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9699261
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7826030
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7826030
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7826030
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7826030
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2329558
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2329558
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2329558
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2329558
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3901926
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3901926
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3901926
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3901926
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3222133
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3222133
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3222133
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3222133
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4585668
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4585668
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4585668
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4585668
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4419117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4419117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4419117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4419117
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5972204
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5972204
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5972204
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5972204
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6999994
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6999994
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6999994
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6999994
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5847701
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5847701
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5847701
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5847701
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7901408
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7901408
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7901408
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7901408
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6840148
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6840148
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6840148
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6840148
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6793822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6793822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6793822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6793822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3605663
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3605663
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3605663
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3605663
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2133848
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2133848
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2133848
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2133848
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2637104
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2637104
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2637104
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2637104
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8336664
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8336664
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8336664
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8336664
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3326140
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3326140
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3326140
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3326140

step	inference rule	input	feed	output	validity (as per SymPy)
5	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9394939493 \(\nabla^2 E( \vec{r},t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r},t)\) 9499428242 \(E( \vec{r},t)=E( \vec{r})\exp(i \omega t)\)		2029293929 \(\nabla^2 E( \vec{r})\exp(i \omega t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r})\exp(i \omega t)\)	LHS diff is -nabla*2pdg0006238(pdg0009472)exp(pdg0001467pdg0002321pdg0004621) + pdg0006238(pdg0009472, pdg0001467) RHS diff is (-partialpdg0006197pdg0007940exp(pdg0001467pdg0002321pdg0004621) + pdg0001467*2pdg0002718(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472)/pdg0001467*2
6	ID: 111649; differentiate with respect to number of inputs: 1; feeds: 1; outputs: 1 Differentiate Eq.~\\ref{eq:#2} with respect to $#1$; yields Eq.~\\ref{eq:#3}.	2029293929 \(\nabla^2 E( \vec{r})\exp(i \omega t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r})\exp(i \omega t)\)	0003232242 \(t\)	4985825552 \(\nabla^2 E( \vec{r})\exp(i \omega t)=i \omega \mu_0 \epsilon_0 \frac{\partial}{\partial t} E( \vec{r})\exp(i \omega t)\)	recognized infrule but not yet supported
2	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8572852424 \(\vec{E}=E( \vec{r},t)\)	no validation is available for declarations
3	ID: 111237; declare guess solution number of inputs: 1; feeds: 0; outputs: 1 Judicious choice as a guessed solution to Eq.~\\ref{eq:#1} is Eq.~\\ref{eq:#2},	8494839423 \(\nabla^2 \vec{E}=\mu_0 \epsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}\)		9499428242 \(E( \vec{r},t)=E( \vec{r})\exp(i \omega t)\)	no validation is available for declarations
4	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	8494839423 \(\nabla^2 \vec{E}=\mu_0 \epsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}\) 8572852424 \(\vec{E}=E( \vec{r},t)\)		9394939493 \(\nabla^2 E( \vec{r},t)=\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} E( \vec{r},t)\)	LHS diff is -nabla*2pdg0006238(pdg0009472, pdg0001467) + pdg0004326 RHS diff is (-partialpdg0006197pdg0007940 + pdg0001467*2)pdg0006238(pdg0009472, pdg0001467)/pdg0001467**2
7	ID: 111649; differentiate with respect to number of inputs: 1; feeds: 1; outputs: 1 Differentiate Eq.~\\ref{eq:#2} with respect to $#1$; yields Eq.~\\ref{eq:#3}.	4985825552 \(\nabla^2 E( \vec{r})\exp(i \omega t)=i \omega \mu_0 \epsilon_0 \frac{\partial}{\partial t} E( \vec{r})\exp(i \omega t)\)	0003232242 \(t\)	1858578388 \(\nabla^2 E( \vec{r})\exp(i \omega t)=- \omega^2 \mu_0 \epsilon_0 E( \vec{r})\exp(i \omega t)\)	recognized infrule but not yet supported
10	ID: 111457; simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	9485384858 \(\nabla^2 E( \vec{r})\exp(i \omega t)=- \frac{\omega^2}{c^2} E( \vec{r})\exp(i \omega t)\)		3485475729 \(\nabla^2 E( \vec{r})=- \frac{\omega^2}{c^2} E( \vec{r})\)	LHS diff is nabla*2(pdg0002718(pdg0001467pdg0002321pdg0004621) - 1)pdg0006238(pdg0009472) RHS diff is pdg00023212(1 - pdg0002718(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472)/pdg0004567*2
11	ID: 111341; declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	3485475729 \(\nabla^2 E( \vec{r})=- \frac{\omega^2}{c^2} E( \vec{r})\)			no validation is available for declarations
9	ID: 111556; substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	4585828572 \(\epsilon_0 \mu_0=\frac{1}{c^2}\) 1858578388 \(\nabla^2 E( \vec{r})\exp(i \omega t)=- \omega^2 \mu_0 \epsilon_0 E( \vec{r})\exp(i \omega t)\)		9485384858 \(\nabla^2 E( \vec{r})\exp(i \omega t)=- \frac{\omega^2}{c^2} E( \vec{r})\exp(i \omega t)\)	LHS diff is nabla*2(-pdg0002718(pdg0001467pdg0002321pdg0004621) + exp(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472) RHS diff is pdg00023212(pdg0002718(pdg0001467pdg0002321pdg0004621) - exp(pdg0001467pdg0002321pdg0004621))pdg0006238(pdg0009472)/pdg0004567*2
1	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8494839423 \(\nabla^2 \vec{E}=\mu_0 \epsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}\)	no validation is available for declarations
8	ID: 111981; declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			4585828572 \(\epsilon_0 \mu_0=\frac{1}{c^2}\)	no validation is available for declarations