Welcome to the Physics Derivation Graph

MESSAGES:

pdg_app/to_review_derivation sympy_validate_step.validate_step: TypeErrorType Tuple cannot be instantiated; use tuple() instead
pdg_app/to_review_derivation sympy_validate_step.validate_step: TypeErrorType Tuple cannot be instantiated; use tuple() instead

Return to navigation page or list derivations

Review coefficient of thermal expansion using the equation of state for an ideal gas

abstract:
reference: https://notendur.hi.is/hj/EE2/HD1lausn.pdf

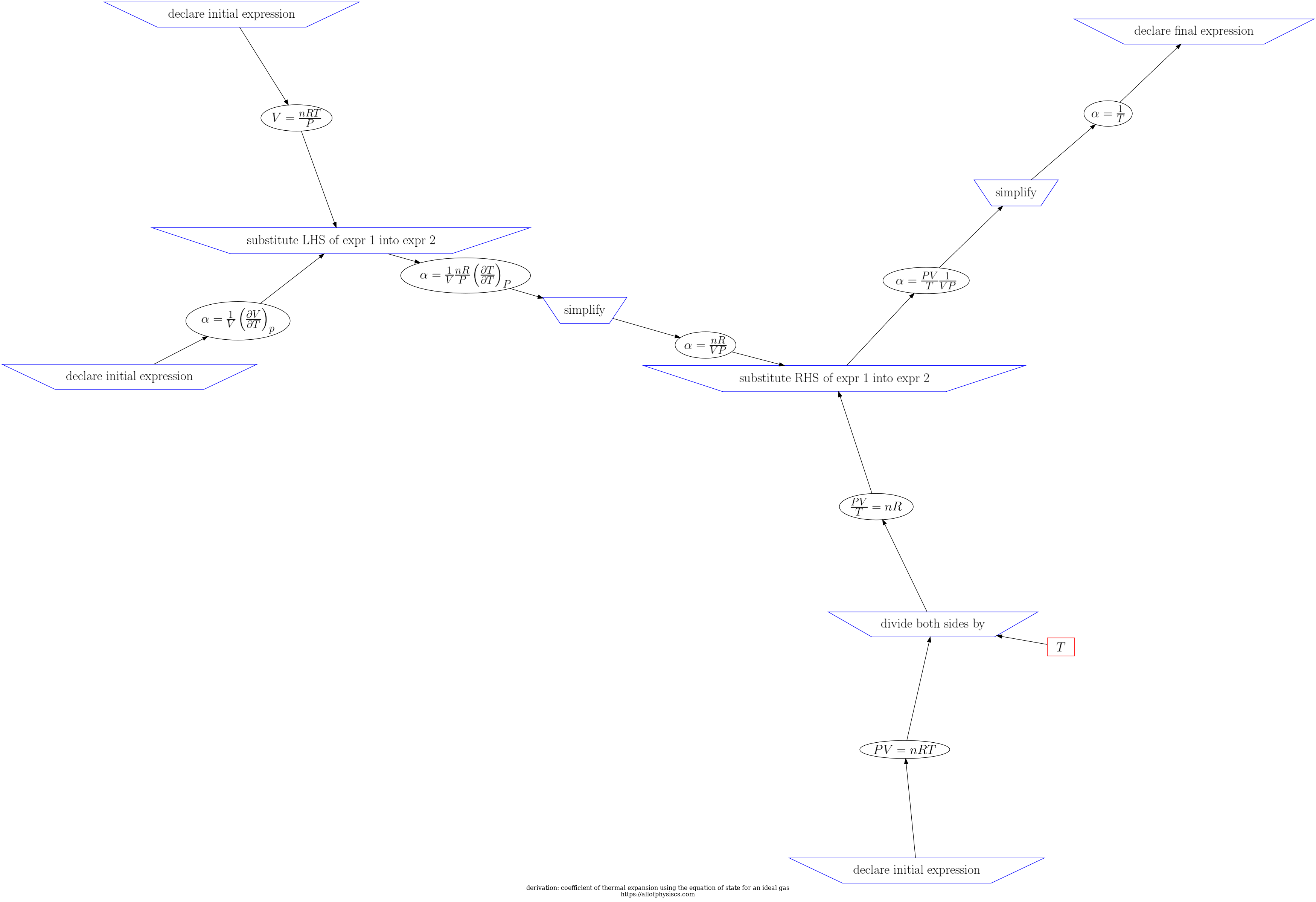
step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3464107376 $\alpha=\frac{1}{V} \left( \frac{\partial V}{\partial T} \right)_p$	no validation is available for declarations
2	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3497828859 $V=\frac{n R T}{P}$	no validation is available for declarations
3	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	3464107376 $\alpha=\frac{1}{V} \left( \frac{\partial V}{\partial T} \right)_p$ 3497828859 $V=\frac{n R T}{P}$		1311403394 $\alpha=\frac{1}{V} \frac{nR}{P} \left( \frac{\partial T}{\partial T} \right)_P$	Type Tuple cannot be instantiated; use tuple() instead
4	111457: simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	1311403394 $\alpha=\frac{1}{V} \frac{nR}{P} \left( \frac{\partial T}{\partial T} \right)_P$		5962145508 $\alpha=\frac{nR}{VP}$	Type Tuple cannot be instantiated; use tuple() instead
5	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8435841627 $P V=n R T$	no validation is available for declarations
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	8435841627 $P V=n R T$	7924842770 $T$	2613006036 $\frac{PV}{T}=nR$	valid
7	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5962145508 $\alpha=\frac{nR}{VP}$ 2613006036 $\frac{PV}{T}=nR$		6925244346 $\alpha=\frac{PV}{T} \frac{1}{VP}$	LHS diff is -pdg0004686 + pdg0007586pdg0008134/pdg0007343 RHS diff is pdg0002834pdg0008179 - pdg0007586*pdg0008134/pdg0007343
8	111457: simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	6925244346 $\alpha=\frac{PV}{T} \frac{1}{VP}$		2472653783 $\alpha=\frac{1}{T}$	LHS diff is 0 RHS diff is (pdg0007586*pdg0008134 - 1)/pdg0007343
9	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	2472653783 $\alpha=\frac{1}{T}$			no validation is available for declarations

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.005 seconds for pdg_app/to_review_derivation: node_properties, derivation 6075653
0.006 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation3247165
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2084544
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2084544
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2084544
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2084544
0.005 seconds for compute/get_dict_of_steps_in_derivation: get_step_has_sequence_index3247165
0.009 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8616219
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8616219
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8616219
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8616219
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1291772
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1291772
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1291772
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1291772
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8234746
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8234746
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8234746
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8234746
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9412575
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9412575
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9412575
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9412575
0.008 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5740367
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5740367
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5740367
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5740367
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1200712
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1200712
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1200712
0.007 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1200712
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6085791
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6085791
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6085791
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6085791
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6493669
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6493669
0.01 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6493669
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6493669
0.003 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation6075653
0.007 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id6075653146432
0.018 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule6075653
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7203787
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7203787
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7203787
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7203787
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6730543
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6730543
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6730543
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6730543
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4131683
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4131683
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4131683
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4131683
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8674808
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8674808
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8674808
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8674808
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3001823
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3001823
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3001823
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3001823
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3105135
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3105135
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3105135
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3105135
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6639982
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6639982
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6639982
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6639982
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2763432
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2763432
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2763432
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2763432
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8368559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8368559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8368559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8368559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4349316
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4349316
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4349316
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4349316
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9082448
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9082448
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9082448
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9082448
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9723846
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9723846
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9723846
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9723846
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1298899
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1298899
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1298899
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1298899
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2107822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2107822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2107822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2107822
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8884562
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8884562
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8884562
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8884562
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1952135
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1952135
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1952135
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1952135
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1580334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1580334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1580334
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1580334
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1170712
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1170712
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1170712
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1170712

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3464107376 \(\alpha=\frac{1}{V} \left( \frac{\partial V}{\partial T} \right)_p\)	no validation is available for declarations
2	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3497828859 \(V=\frac{n R T}{P}\)	no validation is available for declarations
3	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	3464107376 \(\alpha=\frac{1}{V} \left( \frac{\partial V}{\partial T} \right)_p\) 3497828859 \(V=\frac{n R T}{P}\)		1311403394 \(\alpha=\frac{1}{V} \frac{nR}{P} \left( \frac{\partial T}{\partial T} \right)_P\)	Type Tuple cannot be instantiated; use tuple() instead
4	111457: simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	1311403394 \(\alpha=\frac{1}{V} \frac{nR}{P} \left( \frac{\partial T}{\partial T} \right)_P\)		5962145508 \(\alpha=\frac{nR}{VP}\)	Type Tuple cannot be instantiated; use tuple() instead
5	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			8435841627 \(P V=n R T\)	no validation is available for declarations
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	8435841627 \(P V=n R T\)	7924842770 \(T\)	2613006036 \(\frac{PV}{T}=nR\)	valid
7	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	5962145508 \(\alpha=\frac{nR}{VP}\) 2613006036 \(\frac{PV}{T}=nR\)		6925244346 \(\alpha=\frac{PV}{T} \frac{1}{VP}\)	LHS diff is -pdg0004686 + pdg0007586pdg0008134/pdg0007343 RHS diff is pdg0002834pdg0008179 - pdg0007586*pdg0008134/pdg0007343
8	111457: simplify number of inputs: 1; feeds: 0; outputs: 1 Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.	6925244346 \(\alpha=\frac{PV}{T} \frac{1}{VP}\)		2472653783 \(\alpha=\frac{1}{T}\)	LHS diff is 0 RHS diff is (pdg0007586*pdg0008134 - 1)/pdg0007343
9	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	2472653783 \(\alpha=\frac{1}{T}\)			no validation is available for declarations