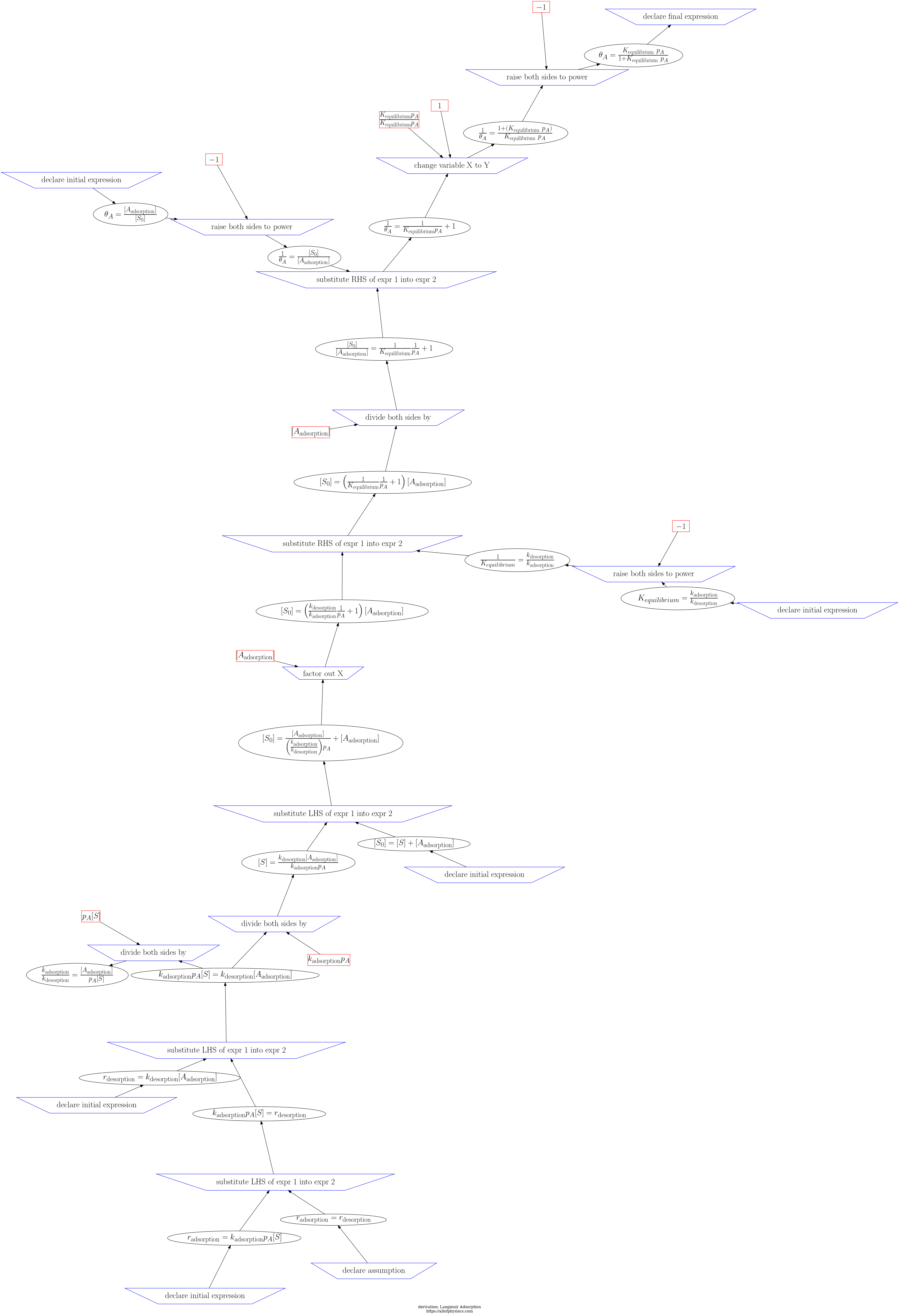
Welcome to the Physics Derivation Graph

Return to navigation page or list derivations

Review Langmuir Adsorption

abstract: from https://arxiv.org/pdf/2210.12150.pdf
reference:

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3736177473 $r_{\rm adsorption}=k_{\rm adsorption} p_A [S]$	no validation is available for declarations
2	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			6955192897 $r_{\rm desorption}=k_{\rm desorption} [A_{\rm adsorption}]$	no validation is available for declarations
3	111104: declare assumption number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an assumption.			6783009163 $r_{\rm adsorption}=r_{\rm desorption}$	no validation is available for declarations
4	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	3736177473 $r_{\rm adsorption}=k_{\rm adsorption} p_A [S]$ 6783009163 $r_{\rm adsorption}=r_{\rm desorption}$		3507029294 $k_{\rm adsorption} p_A [S]=r_{\rm desorption}$	valid
5	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	3507029294 $k_{\rm adsorption} p_A [S]=r_{\rm desorption}$ 6955192897 $r_{\rm desorption}=k_{\rm desorption} [A_{\rm adsorption}]$		3488423948 $k_{\rm adsorption} p_A [S]=k_{\rm desorption} [A_{\rm adsorption}]$	LHS diff is pdg0001966 - pdg0006850pdg0009046pdg0009067 RHS diff is 0
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	3488423948 $k_{\rm adsorption} p_A [S]=k_{\rm desorption} [A_{\rm adsorption}]$	8162179726 $k_{\rm adsorption} p_A$	9562264720 $[S]=\frac{k_{\rm desorption} [A_{\rm adsorption}]}{k_{\rm adsorption} p_A}$	valid
7	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3599953931 $[S_0]=[S] + [A_{\rm adsorption}]$	no validation is available for declarations
8	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9562264720 $[S]=\frac{k_{\rm desorption} [A_{\rm adsorption}]}{k_{\rm adsorption} p_A}$ 3599953931 $[S_0]=[S] + [A_{\rm adsorption}]$		4301729661 $[S_0]=\frac{[A_{\rm adsorption}]}{\left( \frac{k_{\rm adsorption}}{k_{\rm desorption}} \right) p_A} + [A_{\rm adsorption}]$	valid
9	111432: factor out X number of inputs: 1; feeds: 1; outputs: 1 Factor $#1$ from Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	4301729661 $[S_0]=\frac{[A_{\rm adsorption}]}{\left( \frac{k_{\rm adsorption}}{k_{\rm desorption}} \right) p_A} + [A_{\rm adsorption}]$	1268845856 $[A_{\rm adsorption}]$	2168306601 $[S_0]=\left(\frac{k_{\rm desorption}}{k_{\rm adsorption}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]$	valid
10	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	3488423948 $k_{\rm adsorption} p_A [S]=k_{\rm desorption} [A_{\rm adsorption}]$	1945487024 $p_A [S]$	5085809757 $\frac{k_{\rm adsorption}}{k_{\rm desorption}}=\frac{[A_{\rm adsorption}]}{p_A [S]}$	Algebraic error: LHS diff is pdg0006850 - pdg0006850/pdg0008379, RHS diff is pdg0004940(pdg0008379 - 1)/(pdg0009046pdg0009067)
11	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			7924063906 $K_{equilibrium}=\frac{k_{\rm adsorption}}{k_{\rm desorption}}$	no validation is available for declarations
12	111483: raise both sides to power number of inputs: 1; feeds: 1; outputs: 1 Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.	7924063906 $K_{equilibrium}=\frac{k_{\rm adsorption}}{k_{\rm desorption}}$	5516739892 $-1$	6240546932 $\frac{1}{K_{equilibrium}}=\frac{k_{\rm desorption}}{k_{\rm adsorption}}$	recognized infrule but not yet supported
13	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	6240546932 $\frac{1}{K_{equilibrium}}=\frac{k_{\rm desorption}}{k_{\rm adsorption}}$ 2168306601 $[S_0]=\left(\frac{k_{\rm desorption}}{k_{\rm adsorption}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]$		7517073655 $[S_0]=\left(\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]$	valid
14	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	7517073655 $[S_0]=\left(\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]$	5426418187 $[A_{\rm adsorption}]$	6457999644 $\frac{[S_0]}{[A_{\rm adsorption}]}=\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1$	valid
15	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			2114909846 $\theta_A=\frac{[A_{\rm adsorption}]}{[S_0]}$	no validation is available for declarations
16	111483: raise both sides to power number of inputs: 1; feeds: 1; outputs: 1 Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.	2114909846 $\theta_A=\frac{[A_{\rm adsorption}]}{[S_0]}$	7564010952 $-1$	8131665171 $\frac{1}{\theta_A}=\frac{[S_0]}{[A_{\rm adsorption}]}$	recognized infrule but not yet supported
17	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	6457999644 $\frac{[S_0]}{[A_{\rm adsorption}]}=\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1$ 8131665171 $\frac{1}{\theta_A}=\frac{[S_0]}{[A_{\rm adsorption}]}$		7928111771 $\frac{1}{\theta_A}=\frac{1}{K_{\rm equilibrium} p_A} + 1$	LHS diff is 0 RHS diff is pdg0003037/pdg0004940 - 1 - 1/(pdg0004933*pdg0009046)
18	111886: change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.	7928111771 $\frac{1}{\theta_A}=\frac{1}{K_{\rm equilibrium} p_A} + 1$	7630953440 $\frac{K_{\rm equilibrium} p_A}{K_{\rm equilibrium} p_A}$ 6346902704 $1$	7267424860 $\frac{1}{\theta_A}=\frac{1+(K_{\rm equilibrium}\ p_A)}{K_{\rm equilibrium}\ p_A}$	valid
19	111483: raise both sides to power number of inputs: 1; feeds: 1; outputs: 1 Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.	7267424860 $\frac{1}{\theta_A}=\frac{1+(K_{\rm equilibrium}\ p_A)}{K_{\rm equilibrium}\ p_A}$	3911081515 $-1$	4689334676 $\theta_A=\frac{K_{\rm equilibrium}\ p_A}{1+K_{\rm equilibrium}\ p_A}$	recognized infrule but not yet supported
20	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	4689334676 $\theta_A=\frac{K_{\rm equilibrium}\ p_A}{1+K_{\rm equilibrium}\ p_A}$			no validation is available for declarations

Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries:

0.005 seconds for pdg_app/to_review_derivation: node_properties, derivation 5565194
0.01 seconds for compute/get_dict_of_steps_in_derivation: steps_in_this_derivation9905427
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6473958
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6473958
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6473958
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6473958
0.002 seconds for compute/get_dict_of_steps_in_derivation: get_step_has_sequence_index9905427
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1002274
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1002274
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1002274
0.005 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1002274
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6126296
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6126296
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6126296
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6126296
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3002540
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3002540
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3002540
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3002540
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7448863
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7448863
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7448863
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7448863
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3536326
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3536326
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3536326
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3536326
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2741362
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2741362
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2741362
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2741362
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9160268
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9160268
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9160268
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9160268
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2961600
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2961600
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2961600
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2961600
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6255490
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6255490
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6255490
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6255490
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9113516
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9113516
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9113516
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9113516
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9987528
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9987528
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9987528
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9987528
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6119409
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6119409
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6119409
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6119409
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9291151
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9291151
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9291151
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9291151
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2107912
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2107912
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2107912
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2107912
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5162096
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5162096
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5162096
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5162096
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7711815
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7711815
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7711815
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7711815
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6907342
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6907342
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6907342
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6907342
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5451070
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5451070
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5451070
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5451070
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3024471
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3024471
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3024471
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3024471
0.004 seconds for pdg_app/to_review_derivation: get_list_of_step_dicts_in_this_derivation5565194
0.004 seconds for pdg_app/to_review_derivation: get_list_of_sequence_values_for_derivation_id5565194764666
0.018 seconds for pdg_app/to_review_derivation: get_list_node_dicts_of_type inference_rule5565194
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5189348
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5189348
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5189348
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5189348
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9297352
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9297352
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9297352
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9297352
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8402214
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8402214
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8402214
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8402214
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4957820
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4957820
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4957820
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4957820
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2225526
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2225526
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2225526
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2225526
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1011925
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1011925
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1011925
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1011925
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5003353
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5003353
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5003353
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5003353
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9578002
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9578002
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9578002
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9578002
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4948237
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4948237
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4948237
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4948237
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4613966
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4613966
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4613966
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4613966
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6807144
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6807144
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6807144
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6807144
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1883026
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1883026
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1883026
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1883026
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5402082
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5402082
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5402082
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5402082
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7265191
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7265191
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7265191
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7265191
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5955916
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5955916
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5955916
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5955916
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9371298
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9371298
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9371298
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9371298
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4436194
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4436194
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4436194
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4436194
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5838803
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5838803
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5838803
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5838803
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3815535
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3815535
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3815535
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3815535
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7663295
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7663295
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7663295
0.006 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7663295
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule8725392
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT8725392
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED8725392
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT8725392
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule6180689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT6180689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED6180689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT6180689
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3326489
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3326489
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3326489
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3326489
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3539908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3539908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3539908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3539908
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3888507
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3888507
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3888507
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3888507
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7872634
0.004 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7872634
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7872634
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7872634
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2636828
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2636828
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2636828
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2636828
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5494687
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5494687
0.001 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5494687
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5494687
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3513179
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3513179
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3513179
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3513179
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule4268839
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT4268839
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED4268839
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT4268839
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule9068329
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT9068329
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED9068329
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT9068329
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1340243
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1340243
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1340243
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1340243
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5106559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5106559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5106559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5106559
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1473546
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1473546
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1473546
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1473546
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5913332
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5913332
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5913332
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5913332
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule2405992
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT2405992
0.003 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED2405992
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT2405992
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule3959758
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT3959758
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED3959758
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT3959758
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule7023124
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT7023124
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED7023124
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT7023124
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule5571467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT5571467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED5571467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT5571467
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_has_inference_rule1460720
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_INPUT1460720
0.002 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_FEED1460720
0.001 seconds for compute/get_dict_of_steps_in_derivation: step_id_has_expressions, HAS_OUTPUT1460720

step	inference rule	input	feed	output	step validity (as per SymPy)
1	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3736177473 \(r_{\rm adsorption}=k_{\rm adsorption} p_A [S]\)	no validation is available for declarations
2	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			6955192897 \(r_{\rm desorption}=k_{\rm desorption} [A_{\rm adsorption}]\)	no validation is available for declarations
3	111104: declare assumption number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an assumption.			6783009163 \(r_{\rm adsorption}=r_{\rm desorption}\)	no validation is available for declarations
4	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	3736177473 \(r_{\rm adsorption}=k_{\rm adsorption} p_A [S]\) 6783009163 \(r_{\rm adsorption}=r_{\rm desorption}\)		3507029294 \(k_{\rm adsorption} p_A [S]=r_{\rm desorption}\)	valid
5	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	3507029294 \(k_{\rm adsorption} p_A [S]=r_{\rm desorption}\) 6955192897 \(r_{\rm desorption}=k_{\rm desorption} [A_{\rm adsorption}]\)		3488423948 \(k_{\rm adsorption} p_A [S]=k_{\rm desorption} [A_{\rm adsorption}]\)	LHS diff is pdg0001966 - pdg0006850pdg0009046pdg0009067 RHS diff is 0
6	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	3488423948 \(k_{\rm adsorption} p_A [S]=k_{\rm desorption} [A_{\rm adsorption}]\)	8162179726 \(k_{\rm adsorption} p_A\)	9562264720 \([S]=\frac{k_{\rm desorption} [A_{\rm adsorption}]}{k_{\rm adsorption} p_A}\)	valid
7	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			3599953931 \([S_0]=[S] + [A_{\rm adsorption}]\)	no validation is available for declarations
8	111556: substitute LHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	9562264720 \([S]=\frac{k_{\rm desorption} [A_{\rm adsorption}]}{k_{\rm adsorption} p_A}\) 3599953931 \([S_0]=[S] + [A_{\rm adsorption}]\)		4301729661 \([S_0]=\frac{[A_{\rm adsorption}]}{\left( \frac{k_{\rm adsorption}}{k_{\rm desorption}} \right) p_A} + [A_{\rm adsorption}]\)	valid
9	111432: factor out X number of inputs: 1; feeds: 1; outputs: 1 Factor $#1$ from Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	4301729661 \([S_0]=\frac{[A_{\rm adsorption}]}{\left( \frac{k_{\rm adsorption}}{k_{\rm desorption}} \right) p_A} + [A_{\rm adsorption}]\)	1268845856 \([A_{\rm adsorption}]\)	2168306601 \([S_0]=\left(\frac{k_{\rm desorption}}{k_{\rm adsorption}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]\)	valid
10	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	3488423948 \(k_{\rm adsorption} p_A [S]=k_{\rm desorption} [A_{\rm adsorption}]\)	1945487024 \(p_A [S]\)	5085809757 \(\frac{k_{\rm adsorption}}{k_{\rm desorption}}=\frac{[A_{\rm adsorption}]}{p_A [S]}\)	Algebraic error: LHS diff is pdg0006850 - pdg0006850/pdg0008379, RHS diff is pdg0004940(pdg0008379 - 1)/(pdg0009046pdg0009067)
11	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			7924063906 \(K_{equilibrium}=\frac{k_{\rm adsorption}}{k_{\rm desorption}}\)	no validation is available for declarations
12	111483: raise both sides to power number of inputs: 1; feeds: 1; outputs: 1 Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.	7924063906 \(K_{equilibrium}=\frac{k_{\rm adsorption}}{k_{\rm desorption}}\)	5516739892 \(-1\)	6240546932 \(\frac{1}{K_{equilibrium}}=\frac{k_{\rm desorption}}{k_{\rm adsorption}}\)	recognized infrule but not yet supported
13	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	6240546932 \(\frac{1}{K_{equilibrium}}=\frac{k_{\rm desorption}}{k_{\rm adsorption}}\) 2168306601 \([S_0]=\left(\frac{k_{\rm desorption}}{k_{\rm adsorption}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]\)		7517073655 \([S_0]=\left(\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]\)	valid
14	111975: divide both sides by number of inputs: 1; feeds: 1; outputs: 1 Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.	7517073655 \([S_0]=\left(\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1\right)[A_{\rm adsorption}]\)	5426418187 \([A_{\rm adsorption}]\)	6457999644 \(\frac{[S_0]}{[A_{\rm adsorption}]}=\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1\)	valid
15	111981: declare initial expression number of inputs: 0; feeds: 0; outputs: 1 Eq.~\\ref{eq:#1} is an initial equation.			2114909846 \(\theta_A=\frac{[A_{\rm adsorption}]}{[S_0]}\)	no validation is available for declarations
16	111483: raise both sides to power number of inputs: 1; feeds: 1; outputs: 1 Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.	2114909846 \(\theta_A=\frac{[A_{\rm adsorption}]}{[S_0]}\)	7564010952 \(-1\)	8131665171 \(\frac{1}{\theta_A}=\frac{[S_0]}{[A_{\rm adsorption}]}\)	recognized infrule but not yet supported
17	111634: substitute RHS of expr 1 into expr 2 number of inputs: 2; feeds: 0; outputs: 1 Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.	6457999644 \(\frac{[S_0]}{[A_{\rm adsorption}]}=\frac{1}{K_{\rm equilibrium}} \frac{1}{p_A} + 1\) 8131665171 \(\frac{1}{\theta_A}=\frac{[S_0]}{[A_{\rm adsorption}]}\)		7928111771 \(\frac{1}{\theta_A}=\frac{1}{K_{\rm equilibrium} p_A} + 1\)	LHS diff is 0 RHS diff is pdg0003037/pdg0004940 - 1 - 1/(pdg0004933*pdg0009046)
18	111886: change variable X to Y number of inputs: 1; feeds: 2; outputs: 1 Change variable $#1$ to $#2$ in Eq.~\\ref{eq:#3}; yields Eq.~\\ref{eq:#4}.	7928111771 \(\frac{1}{\theta_A}=\frac{1}{K_{\rm equilibrium} p_A} + 1\)	7630953440 \(\frac{K_{\rm equilibrium} p_A}{K_{\rm equilibrium} p_A}\) 6346902704 \(1\)	7267424860 \(\frac{1}{\theta_A}=\frac{1+(K_{\rm equilibrium}\ p_A)}{K_{\rm equilibrium}\ p_A}\)	valid
19	111483: raise both sides to power number of inputs: 1; feeds: 1; outputs: 1 Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.	7267424860 \(\frac{1}{\theta_A}=\frac{1+(K_{\rm equilibrium}\ p_A)}{K_{\rm equilibrium}\ p_A}\)	3911081515 \(-1\)	4689334676 \(\theta_A=\frac{K_{\rm equilibrium}\ p_A}{1+K_{\rm equilibrium}\ p_A}\)	recognized infrule but not yet supported
20	111341: declare final expression number of inputs: 1; feeds: 0; outputs: 0 Eq.~\\ref{eq:#1} is one of the final equations.	4689334676 \(\theta_A=\frac{K_{\rm equilibrium}\ p_A}{1+K_{\rm equilibrium}\ p_A}\)			no validation is available for declarations