MESSAGE:

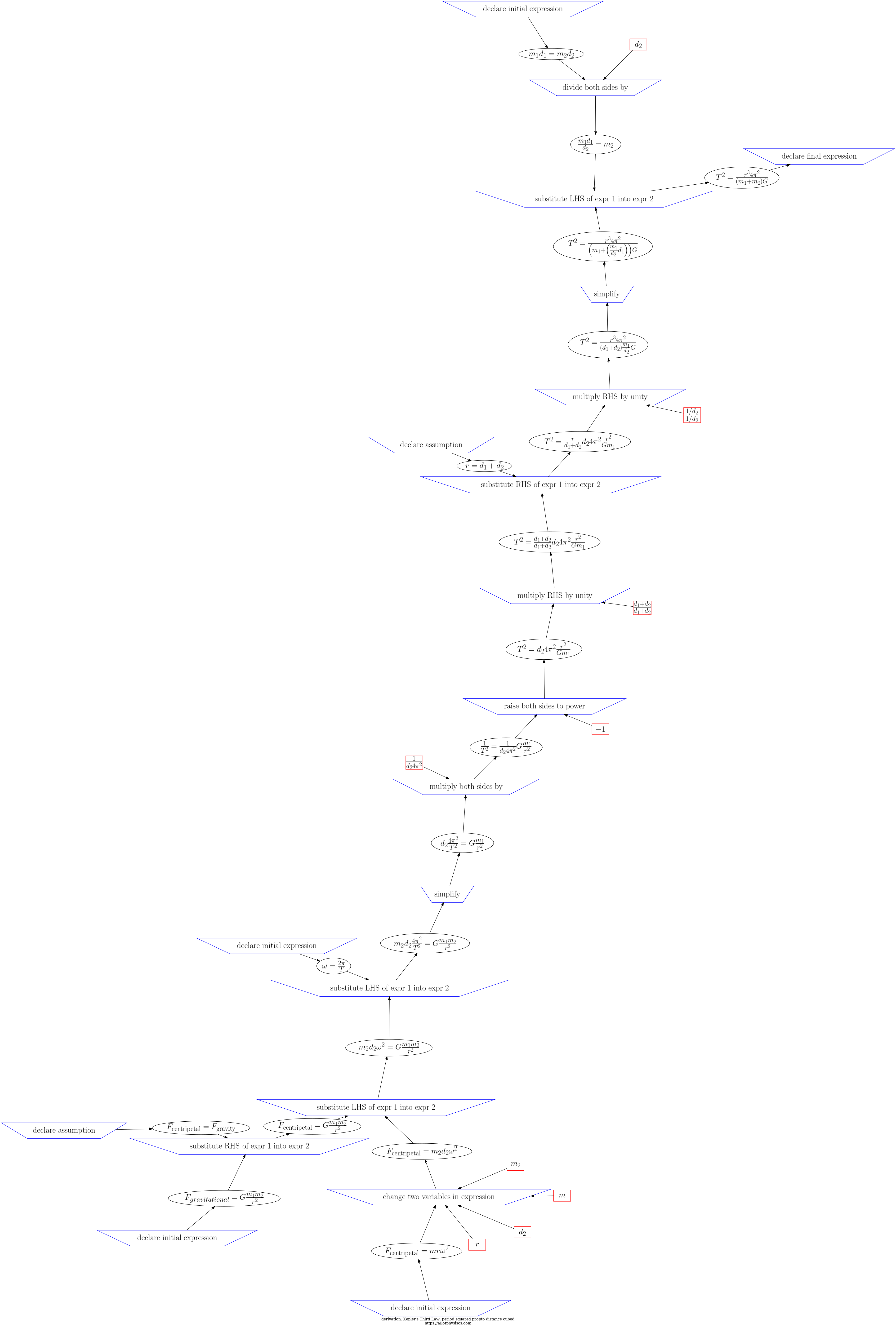
Return to navigation page or list derivations

Review Kepler's Third Law: period squared propto distance cubed

step inference rule input feed output step validity (as per SymPy)
1
  • 111981: declare initial expression
  • number of inputs: 0; feeds: 0; outputs: 1
  • Eq.~\\ref{eq:#1} is an initial equation.
  1. 1292735067
    \(F_{gravitational}=G \frac{m_1 m_2}{r^2}\)
 no validation is available for declarations
2
  • 111981: declare initial expression
  • number of inputs: 0; feeds: 0; outputs: 1
  • Eq.~\\ref{eq:#1} is an initial equation.
  1. 4393258808
    \(F_{\rm centripetal}=m r \omega^2\)
 no validation is available for declarations
3
  • 111984: change two variables in expression
  • number of inputs: 1; feeds: 4; outputs: 1
  • Change variable $#1$ to $#2$ and $#3$ to $#4$ in Eq.~\\ref{eq:#5}; yields Eq.~\\ref{eq:#6}.
  1. 4393258808
    \(F_{\rm centripetal}=m r \omega^2\)
  1. 9884115626
    \(r\)
  1. 1635147226
    \(m_2\)
  1. 1036530438
    \(d_2\)
  1. 8916428651
    \(m\)
  1. 3649797559
    \(F_{\rm centripetal}=m_2 d_2 \omega^2\)
 list index out of range
4
  • 111104: declare assumption
  • number of inputs: 0; feeds: 0; outputs: 1
  • Eq.~\\ref{eq:#1} is an assumption.
  1. 3176662571
    \(F_{\rm centripetal}=F_{\rm gravity}\)
 no validation is available for declarations
5
  • 111634: substitute RHS of expr 1 into expr 2
  • number of inputs: 2; feeds: 0; outputs: 1
  • Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.
  1. 1292735067
    \(F_{gravitational}=G \frac{m_1 m_2}{r^2}\)
  1. 3176662571
    \(F_{\rm centripetal}=F_{\rm gravity}\)
  1. 6829281943
    \(F_{\rm centripetal}=G \frac{m_1 m_2}{r^2}\)
 LHS diff is -pdg0001687 + pdg0002867 RHS diff is pdg0001687 - pdg0004851*pdg0005022*pdg0006277/pdg0002530**2
6
  • 111556: substitute LHS of expr 1 into expr 2
  • number of inputs: 2; feeds: 0; outputs: 1
  • Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.
  1. 3649797559
    \(F_{\rm centripetal}=m_2 d_2 \omega^2\)
  1. 6829281943
    \(F_{\rm centripetal}=G \frac{m_1 m_2}{r^2}\)
  1. 3896798826
    \(m_2 d_2 \omega^2=G \frac{m_1 m_2}{r^2}\)
 valid
7
  • 111981: declare initial expression
  • number of inputs: 0; feeds: 0; outputs: 1
  • Eq.~\\ref{eq:#1} is an initial equation.
  1. 3132131132
    \(\omega=\frac{2\pi}{T}\)
 no validation is available for declarations
8
  • 111556: substitute LHS of expr 1 into expr 2
  • number of inputs: 2; feeds: 0; outputs: 1
  • Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.
  1. 3896798826
    \(m_2 d_2 \omega^2=G \frac{m_1 m_2}{r^2}\)
  1. 3132131132
    \(\omega=\frac{2\pi}{T}\)
  1. 9070394000
    \(m_2 d_2 \frac{4 \pi^2}{T^2}=G \frac{m_1 m_2}{r^2}\)
 LHS diff is pdg0002321 - 4*pdg0002798*pdg0003141**2*pdg0004851/pdg0009491**2 RHS diff is 2*pdg0003141/pdg0009491 - pdg0004851*pdg0005022*pdg0006277/pdg0002530**2
9
  • 111457: simplify
  • number of inputs: 1; feeds: 0; outputs: 1
  • Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.
  1. 9070394000
    \(m_2 d_2 \frac{4 \pi^2}{T^2}=G \frac{m_1 m_2}{r^2}\)
  1. 9838128064
    \(d_2 \frac{4 \pi^2}{T^2}=G \frac{m_1}{r^2}\)
 LHS diff is 4*pdg0002798*pdg0003141**2*(pdg0004851 - 1)/pdg0009491**2 RHS diff is pdg0005022*pdg0006277*(pdg0004851 - 1)/pdg0002530**2
10
  • 111182: multiply both sides by
  • number of inputs: 1; feeds: 1; outputs: 1
  • Multiply both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.
  1. 9838128064
    \(d_2 \frac{4 \pi^2}{T^2}=G \frac{m_1}{r^2}\)
  1. 5684907106
    \(\frac{1}{d_2 4 \pi^2}\)
  1. 9152823411
    \(\frac{1}{T^2}=\frac{1}{d_2 4 \pi^2} G \frac{m_1}{r^2}\)
 valid
11
  • 111483: raise both sides to power
  • number of inputs: 1; feeds: 1; outputs: 1
  • Raise both sides of Eq.~\\ref{eq:#2} to $#1$; yields Eq.~\\ref{eq:#3}.
  1. 9152823411
    \(\frac{1}{T^2}=\frac{1}{d_2 4 \pi^2} G \frac{m_1}{r^2}\)
  1. 7445388869
    \(-1\)
  1. 9170048197
    \(T^2=d_2 4 \pi^2 \frac{r^2}{G m_1}\)
 recognized infrule but not yet supported
12
  • 111646: multiply RHS by unity
  • number of inputs: 1; feeds: 1; outputs: 1
  • Multiply RHS of Eq.~\\ref{eq:#2} by 1, which in this case is $#1$; yields Eq.~\\ref{eq:#3}
  1. 9170048197
    \(T^2=d_2 4 \pi^2 \frac{r^2}{G m_1}\)
  1. 8122039815
    \(\frac{d_1+d_2}{d_1+d_2}\)
  1. 1811867899
    \(T^2=\frac{d_1+d_2}{d_1+d_2} d_2 4 \pi^2 \frac{r^2}{G m_1}\)
 valid
13
  • 111104: declare assumption
  • number of inputs: 0; feeds: 0; outputs: 1
  • Eq.~\\ref{eq:#1} is an assumption.
  1. 5586102077
    \(r=d_1 + d_2\)
 no validation is available for declarations
14
  • 111634: substitute RHS of expr 1 into expr 2
  • number of inputs: 2; feeds: 0; outputs: 1
  • Substitute RHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.
  1. 5586102077
    \(r=d_1 + d_2\)
  1. 1811867899
    \(T^2=\frac{d_1+d_2}{d_1+d_2} d_2 4 \pi^2 \frac{r^2}{G m_1}\)
  1. 2906548078
    \(T^2=\frac{r}{d_1+d_2} d_2 4 \pi^2 \frac{r^2}{G m_1}\)
 LHS diff is 0 RHS diff is 4*pdg0002530**2*pdg0002798*pdg0003141**2*(-pdg0002530 + pdg0002798 + pdg0007652)/(pdg0005022*pdg0006277*(pdg0002798 + pdg0007652))
15
  • 111646: multiply RHS by unity
  • number of inputs: 1; feeds: 1; outputs: 1
  • Multiply RHS of Eq.~\\ref{eq:#2} by 1, which in this case is $#1$; yields Eq.~\\ref{eq:#3}
  1. 2906548078
    \(T^2=\frac{r}{d_1+d_2} d_2 4 \pi^2 \frac{r^2}{G m_1}\)
  1. 9524810853
    \(\frac{1/d_2}{1/d_2}\)
  1. 3781109867
    \(T^2=\frac{r^3 4 \pi^2}{(d_1+d_2) \frac{m_1}{d_2}G}\)
 valid
16
  • 111457: simplify
  • number of inputs: 1; feeds: 0; outputs: 1
  • Simplify Eq.~\\ref{eq:#1}; yields Eq.~\\ref{eq:#2}.
  1. 3781109867
    \(T^2=\frac{r^3 4 \pi^2}{(d_1+d_2) \frac{m_1}{d_2}G}\)
  1. 4188580242
    \(T^2=\frac{r^3 4 \pi^2}{\left(m_1+\left(\frac{m_1}{d_2}d_1\right)\right)G}\)
 valid
17
  • 111981: declare initial expression
  • number of inputs: 0; feeds: 0; outputs: 1
  • Eq.~\\ref{eq:#1} is an initial equation.
  1. 5128670694
    \(m_1 d_1=m_2 d_2\)
 no validation is available for declarations
18
  • 111975: divide both sides by
  • number of inputs: 1; feeds: 1; outputs: 1
  • Divide both sides of Eq.~\\ref{eq:#2} by $#1$; yields Eq.~\\ref{eq:#3}.
  1. 5128670694
    \(m_1 d_1=m_2 d_2\)
  1. 8044416349
    \(d_2\)
  1. 2217103163
    \(\frac{m_1 d_1}{d_2}=m_2\)
 valid
19
  • 111556: substitute LHS of expr 1 into expr 2
  • number of inputs: 2; feeds: 0; outputs: 1
  • Substitute LHS of Eq.~\\ref{eq:#1} into Eq.~\\ref{eq:#2}; yields Eq.~\\ref{eq:#3}.
  1. 2217103163
    \(\frac{m_1 d_1}{d_2}=m_2\)
  1. 4188580242
    \(T^2=\frac{r^3 4 \pi^2}{\left(m_1+\left(\frac{m_1}{d_2}d_1\right)\right)G}\)
  1. 5658865948
    \(T^2=\frac{r^3 4 \pi^2}{(m_1+m_2)G}\)
 valid
20
  • 111341: declare final expression
  • number of inputs: 1; feeds: 0; outputs: 0
  • Eq.~\\ref{eq:#1} is one of the final equations.
  1. 5658865948
    \(T^2=\frac{r^3 4 \pi^2}{(m_1+m_2)G}\)
 no validation is available for declarations


Hold the mouse over a node to highlight that node and its neighbors. You can zoom in/out. You can pan the image. You can move nodes by clicking and dragging.

Actions: Edit Derivation

Generate Tex file or PDF file
   xor   

Delete Derivation and all associated steps

This does not remove expressions, symbols, and operations.

timing of Neo4j queries: